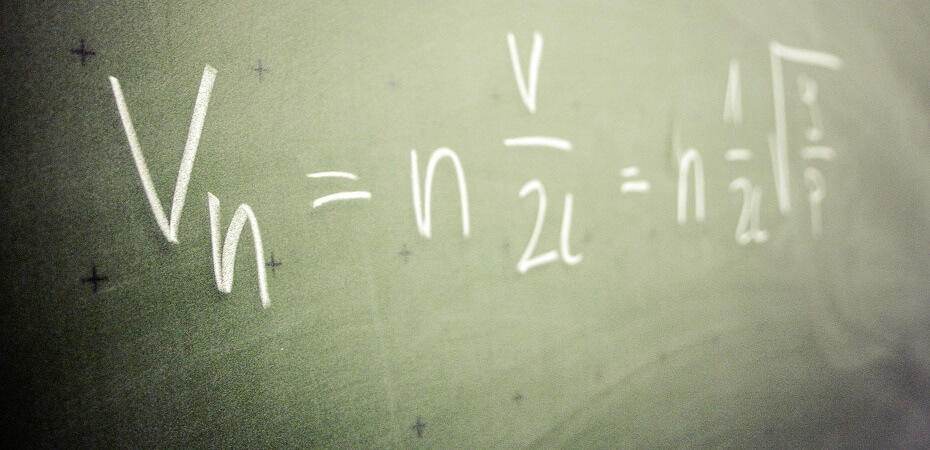Les fractales sont des structures mathématiques fascinantes, caractérisées par l’auto-similarité et une complexité infinie à toutes les échelles.
Théorisées par Gaston Julia, puis popularisées par Benoît Mandelbrot, elles apparaissent aussi bien dans la nature et la géologie, que dans la technologie. Des formes comme le flocon de Koch ou le triangle de Sierpinski révèlent un monde où les mathématiques et l’esthétique se rejoignent harmonieusement.
Voici notre dossier complet sur les fractales mathématiques !
Décoder l’ensemble de Julia : une plongée dans l’infini des fractales
Pour débuter le travail de compréhension des fractales, impossible de ne pas mentionner l'ensemble de Julia, qui a été fondateur dans cette théorisation. Gaston Julia, né en Algérie en 1893, a mené une carrière académique prestigieuse en tant que professeur de mathématiques. Après avoir obtenu son doctorat, il a enseigné à l'École Normale Supérieure, où il a formé plusieurs générations de mathématiciens.
Avant ses travaux, les bases théoriques des ensembles fractals et des systèmes dynamiques se dessinaient déjà au XIXe siècle. Des mathématiciens comme Pierre Fatou, Henri Poincaré et Félix Klein ont exploré les comportements complexes des fonctions holomorphes et des transformations itératives.
On dénombre 4 grands principes faisant partie de l'ensemble de Julia :
- Forme mathématique : L’équation de Julia repose sur l’itération de la fonction quadratique complexe, où ses facteurs sont des nombres complexes.
- Divergence ou stabilité : En appliquant cette fonction de manière répétée à un point z, on observe s’il tend vers l’infini (divergence) ou reste dans une zone limitée (stabilité).
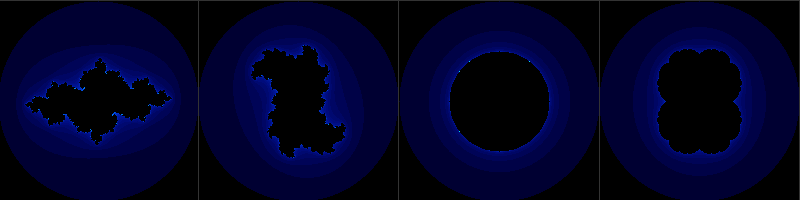
- Définition de l’ensemble : L’ensemble de Julia est formé par les points z dont les itérations ne divergent pas. Sa forme dépend du paramètre c.
- Lien avec Mandelbrot : L’ensemble de Mandelbrot classe les valeurs de c selon la stabilité de leur ensemble de Julia, reliant ainsi les deux structures fractales.
soit un chiffre incommensurable, presque infini
L'ensemble poursuit l'équation suivante :
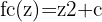
Ces équations se classent en deux grandes catégories :
Les ensembles connexes
Les ensembles totalement disjoints
Ainsi :
- Si
appartient à l’ensemble de Mandelbrot, alors l’ensemble de Julia correspondant est connexe, formant une structure continue. Ces ensembles affichent des formes filamenteuses et riches en détails, rappelant des figures organiques comme des coraux ou des nervures de feuilles. Par exemple, pour 
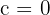, l’ensemble de Julia est un simple disque, tandis que pour des valeurs complexes, il adopte des formes plus tourmentées. - Si n’appartient pas à l’ensemble de Mandelbrot, alors l’ensemble de Julia est totalement disjoint, composé d’un nuage de points séparés, formant ce que l’on appelle une "poussière de Fatou". Ces ensembles présentent des structures éparses où chaque point est isolé des autres.
Des logiciels comme Houdini ou Mandelbulb3D permettent de générer des environnements ultra-détaillés à partir d’équations fractales, offrant une esthétique à la fois réaliste et surnaturelle.
Mandelbrot et l'univers des fractales : histoire et applications fascinantes
"Les Objets Fractals : Forme, Hasard et Dimension" (1975) est l’ouvrage fondateur où Benoît Mandelbrot introduit la notion de fractale, et notamment les fractales de Mandelbrot. L'auteur y explore comment ces formes complexes et irrégulières, présentes dans la nature, obéissent à des règles mathématiques spécifiques.
En reliant géométrie, chaos et structures naturelles, il démontre que les fractales offrent un nouveau langage pour comprendre le monde, influençant de nombreux domaines scientifiques et artistiques
En 1973, Mandelbrot signe un article scientifique qui va changer sa carrière et la perception de ses pairs sur les questions de nombres entiers et de formes définies, ou plutôt, indéfinies : Formes nouvelles du hasard dans les sciences.
L'article se focalise sur :
- L'importance des fluctuations obligatoires
- La non-existence d'une seule forme de hasard, qui conduirait toujours à une égalisation par la loi des grands nombres
- Les phénomènes de la nature obéissent à cet autre type de hasard où l’on ne peut appliquer la loi des grands nombres
- Ces phénomènes répondent plutôt à une hométhie d'échelle, qui sera appelée plus tard "autosimilarité'
Plusieurs principes définissent cet ensemble complexe :
- Connexité
- Autosimilarité
- Universalité
L’ensemble de Mandelbrot fascine par ses motifs esthétiques, mêlant rigueur scientifique et beauté visuelle, créant un lien entre mathématiques et art. L'ensemble a d'ailleurs été source d'inspiration pour le graphisme, la musique et l’animation, où les motifs fractals enrichissent les œuvres numériques grâce à l'image augmentée.
Les travaux de Mandelbrot sont une source d'inspiration et d'innovation depuis les années 1970, et continuent d’influencer la science, l’ingénierie et l’art, ouvrant de nouvelles perspectives en recherche. Parmi les exemples les plus pertinents, on retrouve :
- Benoît Mandelbrot lui-même, en collaboration avec Richard Hudson, a appliqué les fractales à la finance, montrant que les marchés suivent des modèles imprévisibles loin des courbes gaussiennes classiques
- Michael Barnsley, mathématicien, a développé la compression fractale des images, une technique révolutionnaire pour stocker des images en exploitant l’auto-similarité
- Geoffrey West, physicien, a utilisé les fractales pour expliquer les lois d’échelle en biologie, notamment la manière dont les réseaux vasculaires optimisent la distribution des nutriments
Grâce à cette théorie, les fractales sont alors étudiées sous tous leurs angles, y compris dans la nature, avec la végétation et la géologie.
Les fractales dans la nature : de la végétation aux formations géologiques, entre chaos et ordre
Les fractales sont des structures répétitives qui se retrouvent partout dans la végétation.
Des arbres aux feuilles, en passant par les fleurs et les racines, ces formes permettent une croissance optimisée.
Elles favorisent une meilleure absorption de la lumière, une circulation efficace des nutriments et une adaptation aux contraintes environnementales.
Pour comprendre les fractales naturelles, il est important de comprendre que l'on peut les retrouver à différentes échelles de notre quotidien, que ce soit à l'échelle microscopique (pour des flocons de neige) ou bien à grande échelle (pour des nuages ou des montagnes).
Ainsi, on parle de fractales végétales et géologiques pour désigner une réalité qui a été verbalisée par Mandelbrot :
"Les nuages ne sont pas des sphères, les montagnes ne sont pas des cônes, les rivages ne sont pas des arcs de cercle, l'écorce d'un arbre n'est pas lisse et l'éclair ne trace pas de ligne droite. La nature est complexe et la géométrie fractale rend compte de cette complexité et permet de l'étudier"
Benoît Mandelbrot, Une approche fractale des marchés: risquer, perdre et gagner (2005)
Fractales végétales
Dans la nature, la croissance végétale suit souvent des modèles fractals. Ces structures permettent aux plantes d’optimiser leur développement en maximisant l’exposition à la lumière, l’efficacité du transport des nutriments et l’adaptation aux conditions environnementales.
Trois grands ensembles sont alors à distinguer pour des propriétés propres :
🌳 Les arbres et leurs ramifications
🌸 Les fleurs et leurs graines
🍃 Les feuilles et leurs nervures
Les feuilles possèdent des motifs fractals dans leurs systèmes de nervures, qui assurent une distribution efficace de l’eau et des minéraux. Ce réseau optimise aussi la résistance de la feuille et permet une réparation plus rapide en cas de dommage.
Fractales géologiques
Les fractales sont aussi présentes dans de nombreux phénomènes géologiques, révélant l’équilibre entre ordre et chaos dans la nature. Ces schémas répétitifs permettent de mieux comprendre l’évolution du paysage terrestre et d’améliorer les modèles scientifiques liés aux dynamiques géologiques et environnementales.
Un exemple de fractale montagneuse est le massif du Drakensberg, en Afrique du Sud et au Lesotho. Cette chaîne spectaculaire présente des formations rocheuses abruptes qui, vues de loin, révèlent de vastes reliefs dentelés. En s’approchant, on observe que chaque falaise, pic et ravin suit des motifs similaires, se répétant à différentes échelles.
Les formes fractales observées dans la nature ne sont pas le fruit du hasard, mais le résultat de processus géologiques qui transforment progressivement le paysage :
- L’érosion, causée par l’eau, le vent ou la glace, sculpte les montagnes, les vallées et les littoraux en structures irrégulières qui se répètent à différentes échelles
- La sédimentation, qui accumule progressivement des particules transportées par l’eau ou le vent, façonne des deltas fluviaux et des dunes aux formes fractales, avec des motifs se répétant dans les dépôts successifs
- Les réactions chimiques participent à la formation de cristaux et de minéraux arborant des motifs fractals, comme les dendrites de manganèse qui ressemblent à des branches d’arbres
Les fractales jouent un rôle essentiel dans la compréhension et la simulation des phénomènes naturels complexes, y compris pour la météorologie et d'autres disciplines.
Un exemple concret de cette fractale naturelle n'est autre que le flocon de Koch, incarnation de la géométrie fractale.
Flocon de Koch : un voyage au cœur de la géométrie fractale
Le flocon de Koch est une figure emblématique de la géométrie fractale, illustrant l’idée d’une structure infiniment complexe à partir d’un processus simple.
Conçu par Helge von Koch au début du XXème siècle, il repose sur une construction itérative générant une forme auto-similaire.
Le flocon de Koch est construit à partir d’un simple triangle équilatéral, sur lequel un processus d’itération va progressivement ajouter de la complexité. Ce principe, semblable à celui utilisé pour générer le triangle de Sierpinski, repose sur une modification systématique des segments de la figure :
- À chaque étape, chaque segment de la structure est divisé en trois parties égales
- Une pointe triangulaire est ajoutée au centre
- Cela créé ainsi une succession infinie de nouveaux sommets
Plus on applique d’itérations, plus la figure devient complexe, générant une forme qui semble toujours conserver le même aspect général, quel que soit le niveau d’agrandissement
Pour dessiner le flocon de Koch avec un outil comme un logiciel de dessin vectoriel ou un langage de programmation, des outils comme Python avec Turtle, GeoGebra ou Inkscape permettent d’automatiser cette construction en ajustant le nombre d’itérations pour observer la complexité croissante de la fractale.
Si le flocon de Koch possède des applications dans des domaines comme le graphisme et l'informatique, il est aussi réputé pour son lien avec d'autres fractales de la nature, notamment en physique et en biologie. Il est notamment appliqué pour étudier la croissance fractale des matériaux et organismes.
- Dans le domaine de la physique, le flocon de Koch joue un rôle clé dans l’étude de la croissance fractale des matériaux. On le retrouve dans l’étude des surfaces rugueuses, où il permet d’analyser la diffusion de la lumière ou la conductivité thermique
- En physique des plasmas, il aide à modéliser certaines formes complexes de propagation
- En biologie, des schémas similaires se retrouvent dans la formation de certains tissus et organismes, comme les structures osseuses ou les réseaux vasculaires
Une autre fractale avec des propriétés similaires n'est autre que le triangle de Sierpinski !
Les secrets du triangle de Sierpinski : une exploration de cette fractale emblématique
Le triangle de Sierpinski est une fractale découverte en 1915 par le mathématicien polonais Wacław Sierpiński.
Sa construction repose sur un processus itératif simple, qui peut être réalisé à la main ou à l’aide d’un programme informatique.
D’un point de vue mathématique, le triangle de Sierpinski illustre des propriétés fondamentales des fractales, dans la lignée d'autres théories comme l'ensemble de Julia, pionnier en la matière. Il est auto-similaire, ce qui signifie que n’importe quelle partie de la figure est une réplique réduite de l’ensemble.
Sa dimension fractale n’est pas entière, contrairement aux objets géométriques classiques, et elle est calculée par la relation suivante :
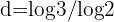, soit environ 1,58 = c'est la dimension de Hausdorff
Les algorithmes permettant de construire les triangles de Sierpinski sont basés sur des règles simples d’itération et de division, ce qui les rend accessibles même à ceux qui ne sont pas experts en mathématiques.
Il existe plusieurs méthodes pour générer cette fractale, mais deux des plus courantes sont :
La méthode de suppression des triangles
La méthode du chaos
Pour plus de détails, consultez notre article détaillé sur le triangle de Sierpinski. Ce triangle populaire a notamment servi de base d'inspiration pour de nombreuses applications, que ce soit dans les télécommunications, les réseaux ou la nature, mais aussi dans le monde de l'animation et des jeux vidéo.
Qu'avez-vous appris des fractales dans ce dossier ?
Vous avez aimé cet article ? Notez-le !
Loading...
