Les mathématiques sont en un sens la poésie des idées logiques.
Albert Einstein
Les mathématiques occupent une place centrale dans notre parcours scolaire mais elles façonnent aussi notre manière de raisonner au quotidien.
Que ce soit pour calculer un pourcentage de réduction, comprendre un graphique dans les médias ou gérer notre budget mensuel, les compétences mathématiques s'avèrent indispensables bien au-delà de la salle de classe.
Pourtant, combien d'élèves et d'étudiants se sentent dépassés cours de math ? Combien pensent "les maths, ce n'est pas pour moi" ? Cette croyance constitue le premier obstacle à surmonter.
Car contrairement aux idées reçues, les mathématiques ne sont pas réservées à une élite de "matheux" nés avec un don particulier. Comme pour n'importe quelle discipline, la réussite en maths repose avant tout sur une méthode adaptée, de la régularité dans l'effort et une approche positive.
Dans cet article, Superprof vous dévoile 14 astuces efficaces pour transformer votre rapport aux mathématiques. Vous découvrirez comment développer à la fois votre confiance et vos compétences.
| Astuce | Titre | Objectif | Actions clés |
|---|---|---|---|
| 1 | Comprendre que tout le monde peut progresser en maths | Changer son état d’esprit et gagner en confiance | Adopter un growth mindset; valoriser l’effort; analyser ses erreurs; remplacer « je suis nul » par « je n’ai pas encore compris » |
| 2 | Développer une logique mathématique efficace | Améliorer le raisonnement et la compréhension | Pratiquer des énigmes; jeux de logique; raisonnement étape par étape; analyse des erreurs |
| 3 | Renforcer ses bases en mathématiques | Combler les lacunes fondamentales | Identifier ses faiblesses; revoir une notion à la fois; refaire des exercices simples; consolider progressivement |
| 4 | Maîtriser le vocabulaire mathématique | Mieux comprendre les consignes | Apprendre les termes clés; créer des fiches; relire régulièrement; surligner les mots importants |
| 5 | Apprendre avec des exercices corrigés | Transformer la théorie en compétences | Faire les exercices sans correction; analyser les erreurs; refaire après 48h; tenir un cahier d’erreurs |
| 6 | Devenir actif en cours de maths | Comprendre dès le cours | Écouter activement; noter les méthodes; poser des questions; anticiper les étapes |
| 7 | Faire appel à un professeur particulier | Bénéficier d’un accompagnement personnalisé | Identifier les blocages; explications adaptées; entraînement sur mesure; préparation aux examens |
| 8 | Organiser son travail en maths | Installer une régularité efficace | Planifier des sessions courtes; espacement; méthode Pomodoro; outils d’organisation |
| 9 | Relire et ficher ses cours de maths | Mémoriser durablement | Relire sous 24h; reformuler; créer des fiches; révisions espacées |
| 10 | Réviser efficacement les mathématiques | Optimiser les révisions | Planifier à l’avance; varier formats et chapitres; expliquer à voix haute |
| 11 | Utiliser les meilleurs livres de maths | Approfondir en autonomie | Choisir un livre adapté; privilégier corrigés; compléter les cours |
| 12 | Revoir les bases avec des cours en ligne | Apprendre à son rythme | Plateformes interactives; vidéos; exercices avec feedback |
| 13 | Comprendre l’utilité des maths au quotidien | Donner du sens | Relier aux usages quotidiens; applications professionnelles; cas concrets |
| 14 | S’inspirer des méthodes asiatiques | Installer rigueur et efficacité | Pratique quotidienne; répétition; rigueur + créativité |

Astuce n°1 – Comprendre que tout le monde peut progresser en mathématiques
"Je suis nul en maths", "je n'ai pas la bosse des maths"... Ces phrases que tant d'élèves se répètent constituent le premier frein à leur progression.
Pourtant, les recherches en neurosciences sont formelles : l'intelligence mathématique n'est pas innée, elle se développe1.
La mentalité de croissance : votre meilleure alliée
Le concept de "growth mindset" développé par la psychologue Carol Dweck révolutionne notre compréhension de l'apprentissage. Les élèves qui croient que leurs capacités peuvent se développer obtiennent de meilleurs résultats que ceux persuadés que l'intelligence est fixe2.
Concrètement, cela signifie que :
L'effort compte plus que le talent : 20 minutes quotidiennes valent mieux qu'un "don" sans pratique.
La répétition construit les connexions neuronales : chaque exercice renforce votre cerveau.
La méthode prime sur l'acharnement : travailler efficacement 30 minutes surpasse 3 heures sans stratégie.

Une étude publiée dans Psychological Science confirme que les élèves exposés à cette mentalité améliorent significativement leurs notes en mathématiques, particulièrement ceux en difficulté.3
L'erreur, votre meilleure formatrice
En mathématiques, l'erreur est formatrice.
Transformez vos échecs en opportunités : analysez vos erreurs, identifiez les types récurrents, célébrez chaque petite victoire. Laurent Schwartz, mathématicien et médaille Fields 1950, insistait sur l'importance de prendre le temps de comprendre plutôt que de chercher à aller vite dans son autobiographie.4
Remplacez "je suis nul en maths" par "je ne maîtrise pas encore cette notion".

Vous pouvez aussi envisager de prendre des cours de maths terminale s pour progresser plus vite.
Astuce n°2 – Développer une logique mathématique efficace
Les mathématiques ne sont pas qu'une affaire de formules à mémoriser : elles reposent avant tout sur une logique rigoureuse. Comprendre cette logique, c'est se donner les clés pour résoudre n'importe quel problème. Bonne nouvelle : cette capacité se développe comme un muscle, par la pratique régulière et variée.
La logique mathématique, c'est raisonner de manière structurée afin de comprendre le "pourquoi" derrière les formules, de détecter ses erreurs et de transférer ses compétences d'un problème à l'autre :
Etape 1
On démarre avec des hypothèses
Etape 2
On suit des étapes cohérentes
Etape 3
On arrive à une conclusion valide
Voici des exemples simples d'entraînement et d'exercices pour pratiquer les maths au quotidien (même 10-15 minutes par jour) :
Les énigmes classiques
Suites logiques (2, 4, 8, 16, ?), problèmes de pesée, énigmes de traversée, carrés magiques, puzzles...
Les jeux de stratégie :
Echecs (anticipation), Sudoku (déduction), jeu de Nim (stratégie pure), Rush Hour (planification)...
Les exercices de raisonnement mathématique :
Démonstrations simples, problèmes ouverts, raisonnement par l'absurde...
Au quotidien, exercez-vous en calculant de tête à la caisse du supermarché par exemple, en estimant des distances et des durées, en optimisant un rangement, en planifiant des trajets... Ces activités variées créent de nouvelles connexions neuronales et renforcent la plasticité cérébrale5.
Pour progresser, voici les principes à respecter :
Une pratique régulière
15 minutes/jour valent mieux que 2 heures/semaine
La variété des exercices
Alternez énigmes, jeux, problèmes
Une difficulté progressive
Du simple vers le complexe
Une analyse de vos erreurs
Chaque échec révèle une faille à combler et permet de progresser
Trouvez ici votre prochain cours de math 3eme.
Astuce n°3 – Renforcer ses bases pour mieux comprendre les mathématiques
En mathématiques, chaque notion s'appuie sur les précédentes. Si vous butez régulièrement, le problème vient souvent d'une lacune antérieure non comblée.
Les notions fondamentales selon votre niveau
1️⃣ Primaire/Début collège :
- Quatre opérations (addition, soustraction, multiplication et division), fractions, nombres décimaux
- Pourcentages et proportionnalité
- Bases de géométrie (périmètres, aires, angles)
2️⃣ Collège :
- Calcul littéral (développer, factoriser)
- Équations du premier degré
- Théorèmes de Pythagore et Thalès
- Puissances et racines carrées
3️⃣ Lycée :
- Fonctions (affines, second degré, exponentielles)
- Trigonométrie et vecteurs
- Probabilités et statistiques
Ces fondamentaux sont cumulatifs : une faiblesse en fractions handicapera votre compréhension des fonctions rationnelles en cours de maths par exemple.
Auto-évaluez-vous pour identifier vos lacunes
Par exemple :
- Calculez 15 x 12
- Simplifiez la fraction 18/24
- Résolvez 3x + 7 = 22
Si vous hésitez plus de 30 secondes, bravo, vous avez identifié une lacune à travailler !
La méthode des fondations pour combler une lacune
Utilisez la technique de reconstruction :
Etape 1
Identifiez LA notion bloquante
Etape 2
Consacrez-lui 2 à 3 sessions de 30 minutes
Etape 3
Repartez du début, même si ça semble facile
Etape 4
Faites des exercices jusqu'à l'aisance
Ne tombez pas dans l'erreur de vouloir tout revoir en même temps. Mieux vaut consolider UNE base à la fois.
Consolider vos bases est l'investissement le plus rentable pour progresser en cours de math 3eme. Une fois ces fondations renforcées, les nouveaux chapitres deviennent soudainement beaucoup plus accessibles !
Pour suivre votre progression, nous vous recommandons de créer un tableau de suivi (sur Excel ou Notion par exemple ou en version papier). Voici un exemple :
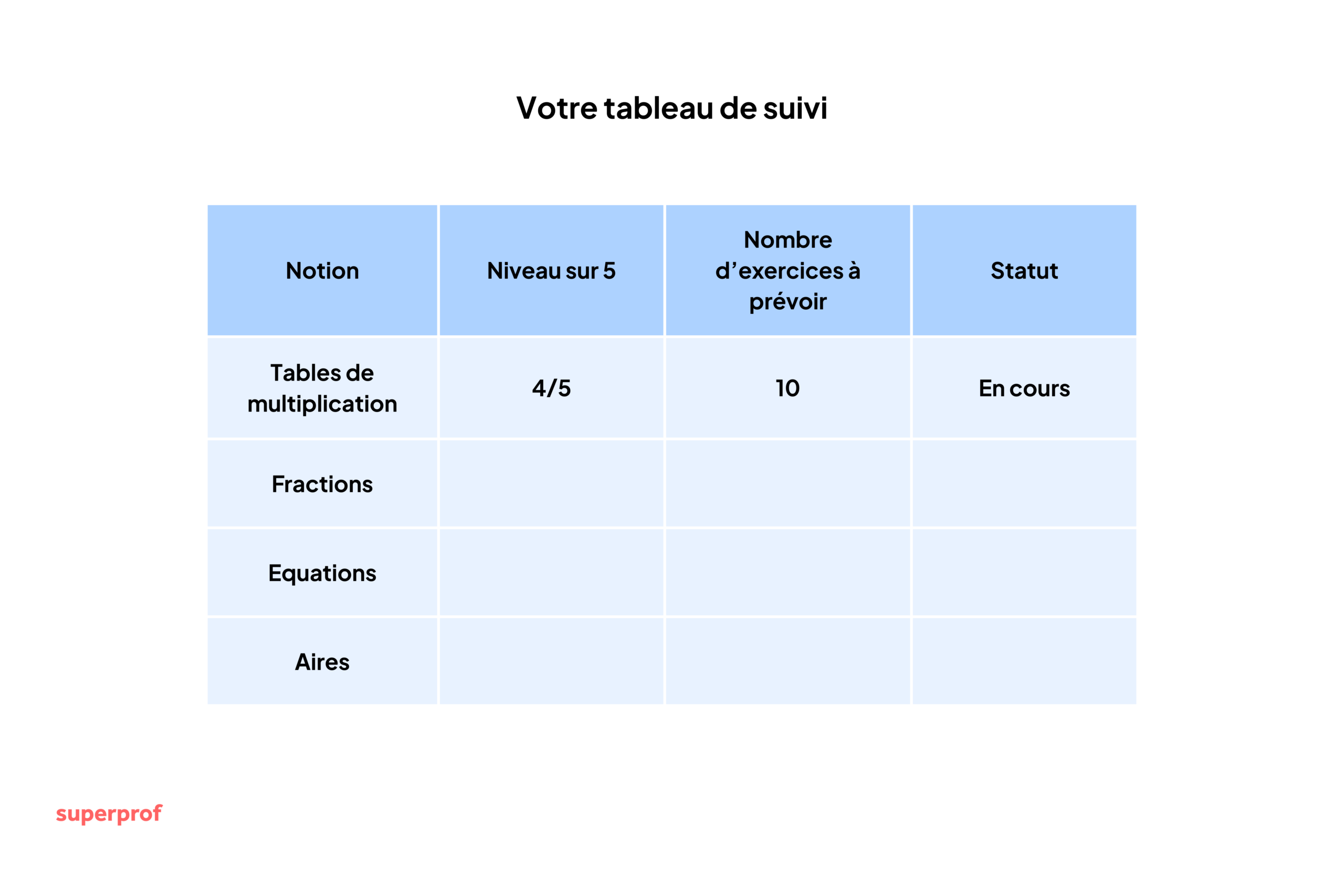
Quelques cours particuliers ciblés identifient rapidement vos "maillons faibles" et vous font gagner des semaines.
Astuce n°4 – Maîtriser le vocabulaire mathématique pour progresser
Beaucoup d'élèves échouent en cours de maths non par manque de compétences, mais par incompréhension des consignes. "Factoriser", "simplifier", "développer" : ces termes désignent des actions précises. Confondre le vocabulaire entraîne une réponse fausse même si vous savez faire.
Le vocabulaire n'est pas accessoire. Bien le comprendre signifie :
🧠 Bien comprendre les énoncés :
"Résoudre l'équation" ≠ "Factoriser l'expression"
😶🌫️ Éviter les confusions :
"produit" vs "somme" changent tout le calcul
✅ Répondre exactement ce qu'on vous demande (et gagner tous les points)
| Terme | Définition | Exemple concret | Usage |
|---|---|---|---|
| Simplifier | Réduire une expression à sa forme la plus simple | 12/18 → 2/3 | Fractions, radicaux |
| Factoriser | Transformer une somme en produit | 3x + 6 → 3(x + 2) | Équations, résolutions |
| Développer | Transformer un produit en somme | 3(x + 2) → 3x + 6 | Calcul littéral |
| Terme | Élément séparé par + ou − | Dans 3x + 5 − 2y : trois termes | Structure d'expressions |
| Produit | Résultat d'une multiplication | Produit de 5 et 3 = 15 | Calculs, équations |
| Quotient | Résultat d'une division | Quotient de 15 par 3 = 5 | Fractions, divisions |
| Somme | Résultat d'une addition | Somme de 7 et 4 = 11 | Calculs, expressions |
| Différence | Résultat d'une soustraction | Différence entre 10 et 3 = 7 | Calculs, problèmes |
| Coefficient | Nombre devant une variable | Dans 5x, le coefficient est 5 | Équations, fonctions |
| Expression | Assemblage de nombres et variables | 2x² + 3x − 1 | Calcul littéral |
| Équation | Égalité avec inconnue(s) à trouver | 2x + 5 = 11 | Résolutions |
| Résoudre | Trouver la(les) valeur(s) de l'inconnue | 2x = 8 → x = 4 | Équations, problèmes |
| Opposé | Nombre de signe contraire | Opposé de 5 = −5 | Calculs relatifs |
| Inverse | Nombre dont le produit vaut 1 | Inverse de 2 = 1/2 | Fractions |
| Périmètre | Longueur du contour d'une figure | Périmètre d’un carré de côté 4 = 16 | Géométrie |
| Aire | Surface intérieure d'une figure | Aire d’un carré de côté 4 = 16 | Géométrie |
| Hypoténuse | Côté opposé à l’angle droit | Triangle rectangle : côté le plus long | Trigonométrie |
Et pour bien ancrer ce vocabulaire, une routine de mémorisation est indispensable :
Etape 1
Créez votre fiche personnelle
Vous pouvez vous aider du tableau ci-dessus
Etape 2
Relisez 5 minutes avant chaque cours de maths
Etape 3
Relisez systématiquement 48h avant chaque contrôle
Etape 4
Testez-vous : cachez les définitions, retrouvez-les
Lors d'un test ou en situation d'exercice, surlignez les mots-clés de l'énoncé et vérifiez que vous savez exactement ce qu'ils signifient. S'il y a une hésitation, retournez à la fiche.
Photographiez votre fiche et consultez-la dans les transports, file d'attente... La répétition espacée ancre définitivement le vocabulaire.
Un travail de mémorisation essentiel pour avoir de meilleures notes en maths !
Astuce n°5 – Apprendre les maths grâce aux exercices corrigés
L'échec est le fondement de la réussite.
Lao Tseu
Les mathématiques ne s'apprennent pas en lisant passivement le cours, mais en FAISANT. Les exercices corrigés constituent votre meilleur outil d'apprentissage pour réussir en cours de maths : ils révèlent vos faiblesses, ancrent les méthodes et transforment la théorie en compétence réelle.
Les exercices permettent de :
Mettre en pratique : passer de "j'ai compris" à "je sais faire"
Tester réellement votre compréhension
Repérer vos erreurs avant le contrôle (c'est mieux que pendant)
Ne vous contentez pas de vérifier si c'est "juste" ou "faux". La correction est un cours à elle seule.
Voici la méthode d'analyse efficace pour éviter l'erreur classique de la lecture passive et du "ah oui, c'était bien ça" :
Etape 1
Faites l'exercice activement SANS regarder la correction (même si difficile)
Etape 2
Comparez votre raisonnement étape par étape avec la correction
Etape 3
Identifiez PRÉCISÉMENT où ça bloque :
Incompréhension de la consigne ? Erreur de calcul ? Méthode inadaptée ? Lacune sur une notion antérieure ?
Etape 4
Refaites l'exercice 48h plus tard jusqu'à une réussite autonome
Etape 5
Notez les pièges rencontrés pour ne plus les reproduire
Créez un "cahier d'erreurs" où vous notez vos fautes récurrentes et leurs solutions. Relisez-le avant chaque test.
La régularité : pratiquer en continu, pas en urgence
L'entraînement de dernière minute ne fonctionne pas en maths. Le cerveau a besoin de répétition espacée pour ancrer les automatismes.
Voici un planning d'entraînement optimal :
Après chaque cours
2-3 exercices d'application directe
15 minutes
En fin de semaine
Des exercices de synthèse du chapitre
30 minutes
1 semaine avant le contrôle
Des exercices types et annales
1 heure
Pendant les vacances
Reprenez les chapitres mal maîtrisés
Quelques ressources d'exercices corrigés par niveau
Collège (6ᵉ à 3ᵉ) :
- Mathenpoche : des exercices interactifs avec corrections détaillées
- Khan Academy : un parcours progressifs avec vidéos explicatives
- Maths-et-tiques : des fiches et des exercices corrigés
Lycée (Seconde à Terminale) :
- APMEP : annales de Brevet et Bac avec corrigés officiels
- Annales2maths : sujets classés par thème et difficulté
- Bibm@th : des exercices corrigés niveau lycée/supérieur
- Kartable (kartable.fr) : des exercices progressifs avec corrections pas à pas
🎓 Ressources universelles :
- Sésamath : des manuels libres avec corrigés intégraux
- Labomep : des exercices personnalisables par votre prof
- YouTube : chaînes Yvan Monka, J'ai 20 en maths, Méthode Maths
- Cahier d'exercices corrigés : Dimathème, Hyperbole, Transmaths...
Créez-vous un planning d'exercices thématiques :
| Jour | Thème | Exercice |
|---|---|---|
| Lundi | Equations | 5 exercices types |
| Mercredi | Géométrie | 3 problèmes + 2 démos |
| Vendredi | Fonctions | Annales bac |
Astuce n°6 – Devenir actif en cours de maths pour mieux comprendre
Le cours de maths est votre première opportunité d'apprentissage : le taux d'échec est réduit de 55 % avec l'apprentissage actif en comparaison avec un cours magistral passif.
en moyenne (6).
Être attentif et comprendre en cours
Écouter le professeur est la première chose à faire. Ne vous contentez pas de copier mécaniquement ce qui est écrit au tableau.
Conseil n°1
Concentrez-vous sur la démarche
pas uniquement le résultat final
Conseil n°2
Repérez les méthodes
"Pour résoudre ce type d'équation, on commence toujours par..."
Conseil n°3
Suivez les démonstrations étape par étape
Pourquoi cette transformation ? Quel théorème justifie cette égalité ?
Conseil n°4
Notez les pièges signalés par le prof
"Attention, erreur fréquente ici..."
Pour une prise de notes efficace, veillez à :
- Structurer visuellement : numérotez les étapes, sautez des lignes, utilisez des couleurs
- Écrire les étapes intermédiaires et pas seulement l'énoncé et la solution
- Noter les POURQUOI entre parenthèses : "(on factorise car...)"
- Créez des encadrés pour les formules/méthodes clés : l'idéal est de tirer un trait à partir de la marge pour avoir un plus grand espace et pourvoir avoir les formules / méthodes en regard de la démonstration.
Vos notes doivent être compréhensibles 3 mois plus tard, sans le prof.
Participer et poser des questions
Participer pendant le cours permet de mieux mémoriser le cours en rentrant chez soi le soir. N'ayez pas peur de poser des questions. Si vous n'avez pas compris quelque chose, il est fort probable que vous ne soyez pas le ou la seul(e).
La participation transforme votre cerveau de récepteur passif en chercheur actif. Les neurosciences montrent que l'engagement actif améliorent significativement les performances.6
Posez des questions dès que vous ne comprenez pas quelque chose
"Pourquoi a-t-on changé de signe ?"
Proposez des réponses, même incertaines
Une erreur corrigée en classe permet de mieux apprendre et plus durablement
Reformulez pour vérifier
"Donc si je comprends bien, on doit d'abord..."
Anticipez mentalement
L'étape suivante avant que le prof l'écrive
Pour aller plus loin
Transformez chaque exemple en "Et si...?"
"Et si le coefficient était négatif ?", "Cette méthode marche-t-elle avec des fractions ?"
L'attention et la participation en classe réduisent drastiquement le temps de révision nécessaire !
Astuce n°7 – Faire appel à un prof particulier pour s’améliorer en maths
Malgré tous vos efforts, certaines notions restent floues ? Un professeur particulier offre un accompagnement sur mesure qui s'adapte à VOTRE façon de comprendre et à vos difficultés en mathématiques.
En classe, le professeur avance au rythme du groupe. En cours particulier, tout s'ajuste à vous. Le cours particulier de maths a donc l'avantage de vous donner des explications ciblées. Le professeur identifie où ça bloque pour reformuler et vous faire comprendre.
Vous disposez d'une correction immédiate et de l'analyse de vos erreurs en direct.
d'apprentissage en moyenne (7)
Le prof particulier comble les lacunes (souvent plusieurs chapitres en arrière), clarifie l'abstrait avec des exemples concrets, propose des exercices sur-mesure, prépare stratégiquement aux examens.
Comment bien choisir votre professeur de maths à domicile ?
Voici les critères essentiels à vérifier :
- Sa pédagogie : reformule-t-il de plusieurs façons ? Utilise-t-il des supports variés ?
- La compatibilité humaine : vous sentez-vous à l'aise pour dire "je ne comprends pas"
- Ses compétences : parcours académique, expérience d'enseignement, spécialisation niveau
- Sa méthodologie : diagnostic initial, plan de progression, exercices entre séances
- Sa disponibilité : horaires compatibles, cours en ligne ou à domicile, possibilité de lui poser des questions entre les cours.
Quand faire appel à un prof de maths particulier ?
N'attendez pas d'être complètement perdu. Intervenir dès les premières difficultés vous permet d'éviter d'accumuler les lacunes. Voici plusieurs situations qui peuvent justifier de faire appel à un prof particulier :
✅ Lacunes persistantes depuis plusieurs chapitres
✅ Passage de cap (entrée au collège, Seconde, Première)
✅ Examen à venir (Brevet, Bac, concours)
✅ Baisse de motivation ou objectif ambitieux
✅ Besoin de méthode (travail sans résultats)

Astuce n°8 – Organiser son travail pour progresser en maths
Vous pouvez avoir toutes les facilités du monde en mathématiques, celles-ci ne seront jamais mieux servies que par un sens certain de l’organisation de vos cours. La recherche montre un avantage clair de l'espacement pour la rétention.8

Ne travaillez pas uniquement avant les tests. Travaillez pour comprendre et mémoriser. Voici un planning régulier et efficace :
| Jour | Activité | Durée |
|---|---|---|
| Lundi | Relire le cours et faire une fiche résumé | 15-20 minutes |
| Mardi | 3-4 exercices d'application | 20-25 minutes |
| Mercredi | Correction détaillée des erreurs | 15 minutes |
| Jeudi | Exercices de difficulté moyenne | 20-25 minutes |
| Vendredi | Révision de la semaine et vocabulaire | 15 minutes |
| Week-end | Exercices de synthèse ou détente ! | 30 minutes ou repos |
Des séances courtes mais fréquentes : la science de la mémorisation
Votre cerveau n'est pas un disque dur. Il oublie naturellement... sauf si vous réactivez régulièrement vos connaissances. Pour les séances courtes et régulières fonctionnent ? Explications :
L'effet d'espacement
Réviser à intervalles croissants ancre durablement (J+1, J+3, J+7, J+15)
Une concentration optimale
Au-delà de 25-30 minutes, l'attention chute drastiquement
Une consolidation nocturne
Le cerveau "range" les infos pendant le sommeil
Moins de fatigue
20 minutes / jour demande un léger effort contrairement à 3h d'affilée qui conduisent à un épuisement mental
25 minutes de travail concentré (sans téléphone, ni notification), puis 5 minutes de pause (se lever, marcher, boire, sortir s'aérer). Après 4 cycles Pomodoro, prenez une vraie pause longue de 20 à 30 minutes (valable lors des longues sessions de révision pré-examen).
Trouvez votre système d'organisation
Il n'existe pas un seul bon outil, seulement celui qui vous convient.
L'agenda papier classique
Pour ceux qui aiment écrire, visualiser la semaine d'un coup d'œil
Notez les chapitres à revoir, les exercices à faire, les dates de contrôles
Le bullet journal personnalisé
Pour les créatifs qui ont besoin de structure flexible
Tracker de révisions (cochez chaque session), listes d'exercices, suivi des notions maîtrisées/à revoir
Les applications numériques
Les adeptes du smartphone (Forest, Todoist, Notion, Google Agenda)
Les rappels automatiques, le suivi de progression, le partage avec le prof particulier
Le planning mural
Pour ceux qui ont besoin de tout voir en grand
Semainier A3 au-dessus du bureau, code couleur (cours/exercices/révisions/contrôles)
Astuce n°9 – Relire et ficher ses cours de maths pour mieux retenir
Assister au cours ne suffit pas. Sans relecture, l'oubli est massif dès les premières heures puis s'accélère les jours suivants. La solution ? Relire et ficher intelligemment.
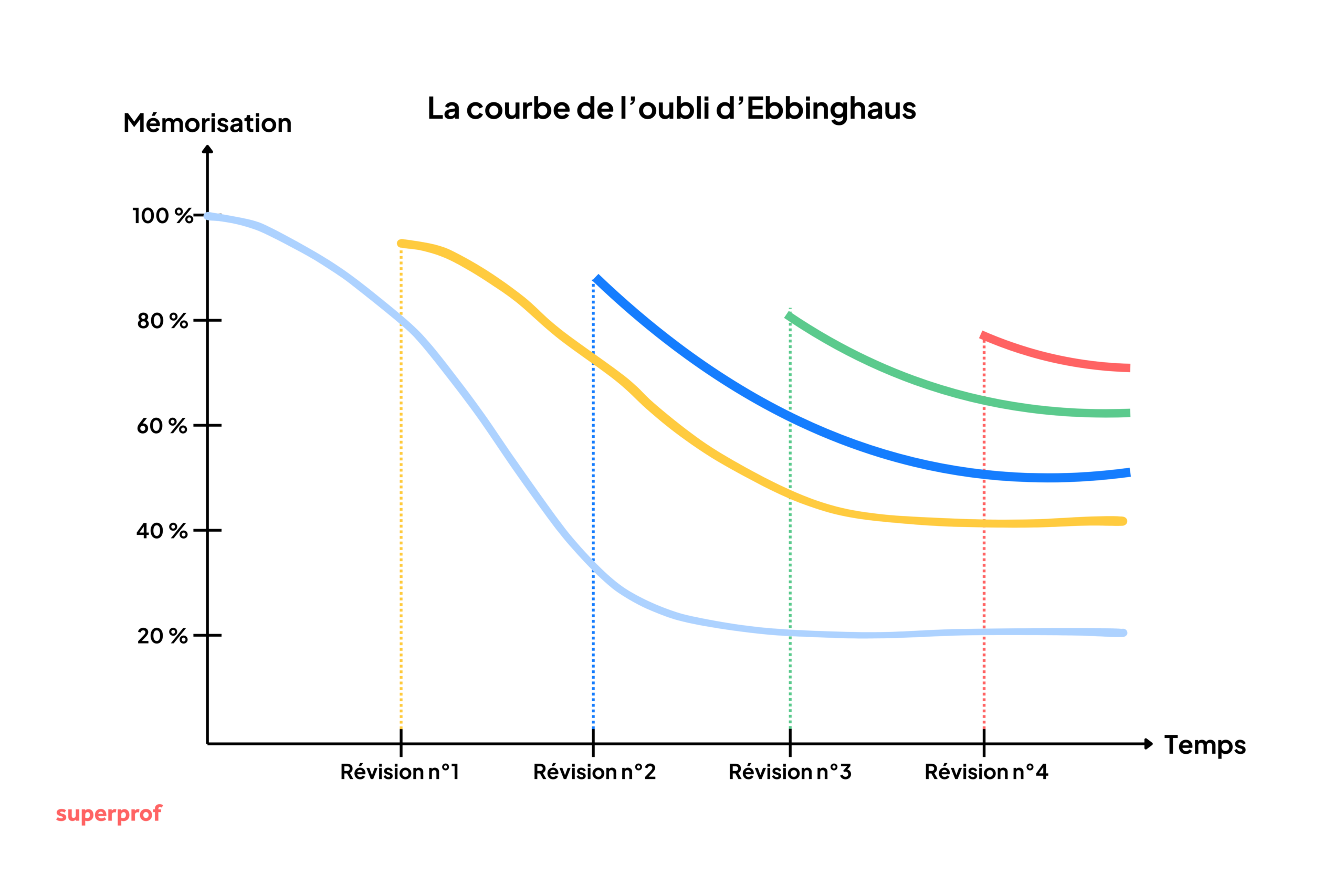
Dans les 24 heures suivant le cours, consacrez 10-15 minutes à une relecture active (le soir même si possible).
✅ Reformulez mentalement chaque partie avec vos propres mots
✅ Identifiez les points clés : théorèmes, formules, méthodes
✅ Repérez ce qui reste flou (à redemander au professeur au prochain cours)
✅ Refaites mentalement un exemple type.
Rédigez une fiche dès que le cours est terminé (une fois par semaine ou une fois par mois par exemple). Voici la structure type d'une fiche efficace :
Définition
Le vocabulaire essentiel
Exemple : Factoriser = transformer une somme en produit
Formules clés
À connaître par cœur
Par exemple : (a+b)² = a² + 2ab + b²
Méthode type
Les étapes d'un exercice classique
Par exemple : Résoudre une équation : isoler x, vérifier
Pièges fréquents
Les erreurs à éviter
Par exemple : -x² ≠ (-x)²
Un travail indispensable pour réussir en mathématiques !
Relisez vos fiches régulièrement pour bien ancrer la leçon avec des révisions proches au début puis en espaçant petit à petit. Par exemple :
- Un jour après la rédaction de votre fiche
- 3 jours après
- 7 jours après
- 15 jours après
- La veille du contrôle
La lecture de la fiche ne suffit pas. Vérifiez immédiatement la compréhension de la leçon en faisant 2 ou 3 exercices pour attester de votre maîtrise réelle.
Astuce n°10 – Réviser efficacement les mathématiques : méthodes et bonnes pratiques
Pour que vous deveniez un pro de la révision, Superprof vous donne ces quelques conseils utiles pour assimiler les mathématiques…
Réviser méthodiquement
La répétition espacée améliore considérablement la rétention à long terme. Au lieu de réviser 3h d'affilée la veille, répartissez : 30 min aujourd'hui, 20 min dans 3 jours, 15 min dans une semaine.
Votre cerveau consolide mieux l'information sur la durée et la recherche montre que cette méthode surpasse systématiquement les révisions groupées. Évitez les marathons de dernière minute : ils créent l'illusion de maîtrise mais favorisent l'oubli rapide.
Organiser ses séances de révisions
Il faut faire des maths tous les jours ! Ce qui est important, c’est de s’organiser des petites sessions très régulièrement, plutôt que de passer une semaine sur les maths et ne plus rien faire après.
Planifiez vos révisions 10-15 jours avant un contrôle. Listez les chapitres concernés, identifiez les difficultés, répartissez le travail.
Alternez les notions pour éviter la confusion : géométrie le lundi, algèbre le mercredi, fonctions le vendredi. Cette variété évite la lassitude.
Varier les rythmes et formats de révision
Avant toute épreuve de mathématiques, que ce soit le brevet, le bac ou bien un concours d'entrée aux grandes écoles, vous devez vous concentrer uniquement sur vos révisions.
Format 1
Lecture de fiches
Format 2
Exercices
Format 3
Vidéos pédagogiques
Format 4
Explications orales à haute voix
Changer de format sollicite différentes zones cérébrales et maintient l'attention. Faites des pauses de 5-10 minutes toutes les 25 minutes (technique Pomodoro) : votre cerveau a besoin de décanter l'information pour mieux la consolider.
Travailler en binôme ou avec un professeur
Expliquer à un camarade est le test ultime de compréhension.
Vous identifiez instantanément vos zones floues. Un professeur particulier détectera quant à lui vos erreurs récurrentes, reformulera autrement, adaptera les exercices. Cette interaction humaine motive et personnalise là où réviser seul peut démotiver.
Votre progression ne sera que meilleure !
S’entraîner à rédiger correctement en langage mathématique
Il est très important de savoir bien rédiger ses démonstrations de mathématiques.
En maths, la forme compte presque autant que le fond. Structurez vos démonstrations (hypothèses → raisonnement → conclusion), utilisez le vocabulaire exact ("donc", "or", "d'où"), sautez des lignes entre les étapes. Les correcteurs valorisent la lisibilité et la logique apparente.
Ce n'est pas parce que vous écrivez en langage mathématique que les fautes d'orthographe ne sont pas pénalisées. Soignez votre orthographe pour ne pas perdre de points.
Soigner la présentation des cours et des fiches
Il est important de bien écrire ses cours de mathématiques pour pouvoir réviser vos cours correctement.
Utilisez des codes couleur, des encadrés , des flèches... Le cerveau retient mieux ce qui est visuel. Par exemple, les définitions en bleu, les formules clés encadrées, la méthode type en vert et les erreurs à éviter en rouge avec une grande croix devant.
Lorsque vous lirez vos cours de maths seconde, les informations les plus importantes vous sauteront aux yeux.
Astuce n°11 – Les meilleurs livres pour devenir bon en maths

Un bon livre est un prof silencieux disponible 24h/24. Mais face aux centaines de références, comment choisir ?
Les critères pour sélectionner le bon ouvrage
Privilégiez la clarté sur l'exhaustivité. Un livre efficace propose :
- Des explications progressives (du simple au complexe),
- Des exercices corrigés détaillés (pas juste la réponse finale),
- Des méthodes explicites (pas seulement de la théorie),
- Et des exemples variés illustrant chaque notion.
Vérifiez que le niveau correspond exactement au vôtre : un livre trop ambitieux décourage, un livre trop simple n'apporte rien.
Notre sélection de livres de maths niveau collège
Nous vous donnons plusieurs ouvrages à consulter pour vous perfectionner en mathématiques :
Vous devriez y trouver quelques astuces pour améliorer votre calcul mental !
Notre sélection d'ouvrages de maths niveau lycée
N'hésitez pas à feuilleter le livre avant d'acheter, que ce soit dans un magasin physique ou en ligne. La plupart des vendeurs en ligne permettent de lire le sommaire et quelques pages avant d'acheter.
Notre sélection de livres de maths niveau supérieur (prépa, université)
Vous avez différentes options pour vous procurer vos ouvrages :
- Neuf : FNAC, Cultura, Amazon, librairies spécialisées (Gibert Joseph).
- D'occasion : Vinted, Leboncoin, Momox, sites de revente entre étudiants.
- Numérique : versions PDF souvent moins chères (Numilog, Google Play Livres).
- Gratuit : bibliothèques universitaires, Sésamath, ressources libres (CultureMath).
Astuce n°12 – Revoir les bases en maths avec des cours en ligne
Pour comprendre les mathématiques, il existe plusieurs méthodes dont les cours de maths en ligne ! Des sites internet proposant une base de données extraordinaire qui vous permettront de comprendre les maths.
Utiliser des plateformes interactives
Khan Academy propose un parcours complet du primaire au supérieur avec des vidéos courtes, des exercices autocorrigés et un système de progression. Chaque notion débloque la suivante, créant une motivation par paliers.
Lumni (France Télévisions) offre des cours officiels alignés sur les programmes, parfaits pour réviser chapitre par chapitre.
Mathenpoche et Kwyk permettent de s'entraîner avec un feedback immédiat : vous tapez votre réponse, le système corrige instantanément et explique l'erreur. Les QCM interactifs identifient rapidement vos zones faibles et vous orientent vers les exercices adaptés.
Regarder des vidéos explicatives
Yvan Monka est un professeur expérimenté qui a une chaîne YouTube intitulée "Maths et Tiques", donnant des explications claires du collège à la Terminale, avec des exemples concrets et une progression logique.
Mickaël Launay de la chaîne Micmaths vulgarise les mathématiques avec des animations visuelles, idéales pour comprendre les concepts abstraits (exponentielles, intégrales, géométrie).
J'ai compris.com propose des vidéos courtes (5-10 min) ciblant une difficulté précise.
C'est que vous pouvez mettre en pause, revenir en arrière, revoir jusqu'à assimilation complète (ce qui est impossible en classe).
Consulter des sites de préparation aux examens
Des sites vous permettent de vous préparer sereinement aux examens :
- Annabac : sujets du Brevet et du Bac corrigés détaillés, fiches de révision, exercices types par thème.
- Studyrama et L'Etudiant compilent les annales avec barèmes et méthodologies.
- MathsLibres génère des exercices personnalisés selon votre niveau.
Ces sites vous familiarisent avec les formats d'épreuves (type de questions, présentation, temps imparti) et transforment l'examen en terrain connu plutôt qu'en surprise. S'entraîner sur des sujets réels est la meilleure préparation possible.
Astuce n°13 – Comprendre que les maths servent dans la vie quotidienne et professionnelle

"À quoi ça sert les maths ?"
Cette question disparaît quand on réalise que les mathématiques structurent notre quotidien.
Que ce soit pour pratiquer un métier, faire ses courses, acheter un appartement… Il y a des tas de raisons de comprendre les maths, de les assimiler et de les pratiquer !
Découvrons ensemble quelques domaines où les maths sont hautement importantes dans notre société moderne…
Les maths dans la vie de tous les jours
Chaque achat sollicite les mathématiques :
- Calculer une réduction de 30 %, estimer si votre budget suffit, vérifier sa monnaie à la boulangerie
- Gérer vos finances mobilise les pourcentages (taux d'intérêt bancaire), les proportionnalités (remboursement de prêt), les statistiques (comparer des offres).
- Cuisiner : respect des proportions et conversions (doubler une recette, convertir des grammes en millilitres).
- Bricoler requiert la géométrie (surface à peindre, découpe d'angles).
- Organiser un voyage fait appel à un calcul mental permanent (distances, temps, coûts, taux de change).
Sans les maths, impossible de négocier, d'économiser ou d'anticiper.
Autant de bonnes raisons de comprendre les maths. Vous ne vous ferez pas arnaquer par un vendeur ou encore vous comprendrez votre banquier quand il vous parlera de taux d'intérêts.
Les maths dans les technologies et le numérique
Pas de révolution numérique sans mathématiques :
Votre smartphone fonctionne grâce aux mathématiques
Algorithmes de compression (photos, vidéos)
Mais aussi cryptographie (sécurité bancaire) et géolocalisation (triangulation GPS)
L'intelligence artificielle repose sur les statistiques et l'algèbre linéaire
La reconnaissance faciale
Mais aussi les recommandations Netflix ou encore les assistants vocaux
La création d'applications et de sites web
Les développeurs utilisent la logique combinatoire
Mais aussi les structures de données et l'optimisation.
Les data scientists analysent milliards de données
Avec des probabilités et la modélisation
Les jeux vidéo simulent la réalité
Via des équations différentielles
Grâce aux mathématiques, on peut prévoir la météo, faire évoluer les réseaux internet, optimiser des opérations de maintenance…
Les maths dans les métiers scientifiques ou médicaux
Evidemment, les mathématiques sont utiles dans le milieu médical.
- Les médecins calculent les dosages médicamenteux (proportions selon poids/âge), interprètent les statistiques d'essais cliniques, utilisent des probabilités pour leurs diagnostics (tests de dépistage, risques).
- Les biologistes analysent des données génétiques par statistiques avancées.
- Les physiciens décrivent l'univers avec des équations (relativité, mécanique quantique).
Il faut maîtriser les maths pour sauver des vies. Bonne motivation, non ?
Astuce n°14 – S’inspirer des méthodes asiatiques en mathématiques
Singapour, le Japon et la Corée du Sud occupent les 3 premières positions des résultats mathématiques selon le PISA (Program for International Student Assessment)10 en 2022, un sondage international comparant les systèmes d'éducation à travers le monde (les résultats du prochain PISA sont attendus pour septembre 2026).
Les élèves asiatiques dominent les classements internationaux pas par "talent génétique", mais grâce à des méthodes pédagogiques éprouvées. Adaptez ces stratégies pour transformer votre apprentissage.
Rigueur, répétition et travail régulier
La méthode japonaise (Kumon) repose sur des micro-progressions quotidiennes : 20 minutes d'exercices ciblés chaque jour avec une augmentation graduelle de la difficulté et une répétition jusqu'à automatisation.
Entre l'âge de 7 et 8 ans, les Japonais apprennent par coeur les tables de multiplication en utilisant la méthode kuku 九九. C'est une chanson répertoriant les tables de multiplication de 1 à 9 et ils doivent la chanter le plus vite possible. Il y a même des concours entre les élèves pour savoir qui est capable de rapper le plus vite les 81 lignes des tables kuku.
Les Japonais utilisent aussi la philosophie du "Kaizen" (amélioration continue) : progresser quotidiennement plutôt que viser 100 % immédiatement.
La mentalité de l'effort prime sur le talent inné. Les élèves japonais refont 5 à 10 fois le même type d'exercice avant de passer au suivant, créant des automatismes solides. La discipline et la régularité sont la garantie de l'excellence.
D'autres cours en écoles privées utilisent la méthode du boulier pour enseigner les opérations aux étudiants. Cette méthode de manipulation permet de rendre plus concrète l'opération et donc de l'ancrer plus facilement dans sa mémoire.
Le but étant de basculer progressivement vers l'utilisation d'un boulier mental pour performer en calcul mental : l'élève s'imagine déplaçant les boules du boulier pour trouver la solution de l'opération.
Les jeunes Japonais à l'école primaire ont 4 séances de mathématiques par semaine de 45 minutes.
Approches pédagogiques variées : exercices, problèmes concrets, compréhension intensive
La méthode singapourienne combine :
La manipulation concrète (cubes, barres numériques)
Les représentations visuelles (schémas en barres)
L'abstraction mathématique.
Les problèmes partent du réel : "3 enfants partagent 12 bonbons" avant d'introduire "12 ÷ 3". L'enseignement spiralaire revisite chaque notion plusieurs fois avec une complexité croissante.
Singapour privilégie la profondeur sur l'étendue : moins de chapitres, mais une maîtrise absolue de chacun. L'interactivité est centrale : des débats mathématiques sont organisés en classe, plusieurs méthodes de résolution sont explorées et la créativité est valorisée.
Combiner rigueur et créativité pour progresser efficacement
Et si l'idéal était un mélange des deux méthodes asiatiques ? La rigueur sans créativité n'est pas très excitante mais la créativité sans rigueur peut vite être chaotique.
On vous recommande :
- Des exercices structurés pour avoir des bases solides avec des séances de calcul mental pour développer des automatismes
- Des séances "découverte" avec des énigmes, des défis, des problèmes ouverts, des casse-têtes pour encourager votre curiosité.
D’autres astuces pour s’améliorer en maths

Comme on est plutôt sympa chez Superprof, on vous laisse avec quelques astuces en plus pour vous améliorer encore et toujours en mathématiques :
Faites tous vos devoirs
C'est ce qui vous permet d'appliquer ce que vous avez vu en cours et de savoir ce que vous n'avez pas compris ou assimilé
Ne manquez aucun cours
Vous risquez de prendre du retard sur un concept et de mal l'assimiler par la suite.
Trouvez un partenaire de travail en maths
A deux, on arrive davantage à se motiver et si l'un n'a pas compris quelque chose, il pourra l'expliquer à l'autre
Demandez de l'aide rapidement
N'attendez pas de vous trouver totalement submergé avant de demander de l'aide.
Dès les premiers signes d'incompréhension, n'hésitez pas ! Reconnaître qu'on a besoin d'aide est un signe d'intelligence.
Posez des questions
Ne vous empêchez pas de demander une explication supplémentaire en cours, il n'y a pas de question bête !
Les mathématiques ne sont pas réservées à une élite : tout le monde peut progresser avec la bonne méthode. Voici un récapitulatif rapide pour transformer votre rapport aux maths :
📈 Adoptez une mentalité de croissance
🏠 Consolidez vos bases
🗣️ Maîtrisez le vocabulaire
💪 Pratiquez régulièrement avec des exercices corrigés
✋ Participez activement en cours
🗺️ Organisez-vous efficacement
📇 Fichez et relisez
📖 Révisez méthodiquement
🧮 Inspirez-vous des méthodes pédagogiques performantes (Singapour, Japon).
Découvrez aussi comment les maths s'appliquent au quotidien et dans les métiers, pour donner du sens à votre apprentissage.
Si en suivant tous ces conseils, vous ne devenez pas la bosse des maths, on ne sait plus quoi faire !
Sources
- Boaler, Jo. Mathematical Mindsets: Unleashing Students' Potential through Creative Math, Inspiring Messages and Innovative Teaching. Jossey-Bass, 2016. Disponible à https://www.researchgate.net/publication/309213995_Mathematical_mindsets_unleashing_students'_potential_through_creative_math_inspiring_messages_and_innovative_teaching.
Consulté le 21 janvier 2026 - Dweck, Carol S. Mindset: The New Psychology of Success. Random House, 2006. Disponible à https://cdn.bookey.app/files/pdf/book/fr/changer-d%E2%80%99%C3%A9tat-d%E2%80%99esprit.pdf. Consulté le 21 janvier 2026
- Paunesku, David, et al. "Mind-Set Interventions Are a Scalable Treatment for Academic Underachievement." Psychological Science. Disponible à https://pubmed.ncbi.nlm.nih.gov/25862544/. Consulté le 21 janvier 2026
- Schwartz, Laurent. Un mathématicien aux prises avec le siècle. Odile Jacob, 1997
- Doidge, Norman. The Brain That Changes Itself. Penguin Books, 2007
- Freeman, Scott, et al. "Active Learning Increases Student Performance in Science, Engineering, and Mathematics." Proceedings of the National Academy of Sciences. Disponible à https://www.pnas.org/doi/10.1073/pnas.1319030111. Consulté le 21 janvier 2026
- Education Endowment Foundation. "One to One Tuition: Moderate Impact for Moderate Cost." Teaching & Learning Toolkit, 2021. Disponible à educationendowmentfoundation.org.uk/education-evidence/teaching-learning-toolkit/one-to-one-tuition. Consulté le 21 janvier 2026
- Cepeda, Nicholas J., et al. "Distributed Practice in Verbal Recall Tasks: A Review and Quantitative Synthesis." Psychological Bulletin. Disponible à https://pubmed.ncbi.nlm.nih.gov/16719566/. Consulté le 21 janvier 2026
- Ebbinghaus, Hermann. Memory: A Contribution to Experimental Psychology. Teachers College Press, 1913.
- OCDE, Résultats du PISA 2022 (Volume I) : Apprentissage et équité dans l'éducation. Disponible à https://www.oecd.org/fr/publications/2023/12/pisa-2022-results-volume-i_76772a36.html. Consulté le 16 janvier 2026
Résumer via IA :

















Bonjour. Mon nom est Tikama, je suis élève en classe de Terminale (série scientifique). Je voudrais acquérir les méthode de travail pour la préparation au bac général… Comment devenir excellent dans toutes les matières (maths, physique-chimie, svt…et bien d’autres comme l’histoire…) ?
Bonjour Tikama :)
Votre question est assez spéciale… En effet, dur d’être bon partout. Nous avons tous des points forts et points faibles au lycée ! Mais pourquoi ne pas tenter de prendre un professeur particulier dans les matières où vous êtes le moins fort ?
Ça ne m’a pas aider pour devenir bon
J’arrive pas à croire merci beaucoup Superprof ! Je suis devant les réponses à mes quelques questions concernant les mathématiques que j’adore ! !
Bonjour a vous tous ici superprof
J’ai beaucoup de misère en mathématique. J’aimerais avoir d l’aide sur sa. Cat savais 4 examen que je n’arrive pas a reussir.
Merci
Merci beaucoup
Bonsoir, je m’appelle aubain, je suis élève en classe de Terminale ( série commerciale) , je prépare le BAC technique, comment je peux faire pour être doué dans tous mes matières ( mathématiques général, technique commerciale, comptabilité générale et analytique, maths financières et statistiques, français etc….), sa me fera plaisir si vous pouvez m’apporter vos conseils
Bonjour Aubain,
Afin de réussir toutes les matières de votre série commerciale, vous pouvez commencer par acheter ou emprunter des manuels scolaires afin de vous entraîner aux différents exercices. Vous pourrez également y trouver des leçons expliquées de manière différente de vos cours habituels.
Si les difficultés persistent, peut-être devriez-vous réfléchir à demander de l’aide à un professeur particulier ? Superprof propose de nombreux profils qui vous permettront de vous aider dans cette démarche.
Nous vous souhaitons bon courage pour votre cursus !
Bonjour je m’appelle charnelle et je suis en 2s et j’ai depuis toujours eu des problèmes en maths bien que la plus part du temps j’avais la moyenne partout sauf dans cette matiere j’aimerais savoir comment y remédier. Cette année je pense que je vais reprendre la classe mais pour y échapper je dois rapidement remonter ma moyenne et ça dans pratiquement toute les matières. J’ai besion d’aide s’il vous plaît.
Bonjour Charnelle,
Pour remonter vos notes en mathématiques et dans l’ensemble des matières vous pouvez commencer par utiliser des manuels scolaires afin de vous entraîner via des exercices et leurs corrigés. De nombreuses applications permettent également de réviser ses cours et de progresser tout en s’amusant. N’hésitez pas à parler de vos difficultés avec vos professeurs, peut-être auront-ils des conseils pour vous. Enfin, vous pouvez également demander de l’aide à un professeur particulier afin qu’il vous accompagne dans l’aide aux devoirs et vous remotive si nécessaire.
Bon courage à vous
Bonjour je m’appelle Siga merci beaucoup superprof pour les conseils je suis en premier s2 et j’ai des lacunes en maths voir bcp je me fait plus confiance je vais reprendre la classe à cause des maths j’aimerai bcp avoir votre aide à cette instant je sais plus quoi faire à voir si je dois changer de série ou bien mais je veux pas changé de série mais je veux pas aussi redoubler
Bonjour Siga,
Merci pour votre commentaire. Vous pouvez reprendre les mêmes conseils évoqués ci-dessus (dans le commentaire précédent). Pour remonter vos notes, le meilleur conseil que je puisse vous donner est de vous entraîner à réaliser des exercices types. Une fois que vous aurez compris le mécanisme de ces exercices, il vous sera plus facile d’y répondre. Au début cela sera difficile. Essayez donc de vous faire accompagner par un ami fort en maths ou bien un professeur. Et surtout ne lâchez pas. Prenez des exercices dans les manuels et regardez ensuite le corrigé pour repérer ce que vous ne comprenez pas.
Bon courage à vous
comme tu voilà
Je suis en terminale C et Mes professeur disent que suis agiter et désordonné. Je raté les choses les plus basique pourtant je les connais
Moi aussi mon prof de maths me le dit souvent..il dit que je suis bête
Bonsoir super prof. Je suis en tles c et je reprends la classe. Les mathématiques me dérangent beaucoup et j’arrive pas souvent à me concentrer. Besoin d’aide je vous en prie !!
Bonjour,
Pour vous accompagner en maths, vous pouvez faire appel à un professeur particulier de mathématiques. Vous pouvez également demander de l’aide à un de vos amis ou bien au professeur. Essayez de refaire les exercices déjà fait en classe pour faciliter l’apprentissage.
Bien à vous
Bonjour j’aime
Merci beaucoup pour votre aide précieux superprof
Maths c’est la vie
Tres efficace pour nous les etudiants merci bien pour vos conseils avisées
Salut je m’appelle Albert .je prépare le cap electricité . Que ferai – je pour être bon en maths , electrotechnique , schema électrique et pct !
Je cherche quelqu’un qui peut me aider devenir un bon maths
Merci beaucoup.je Langevin en classe de première scientifiques,je voulais aussi savoir comment on peut être intéligent aux matières comme la physique et la chimie.
Bonjour,
Je vous conseille de réaliser le plus d’exercices possibles dans ces matières et de chercher à comprendre où vous faites des erreurs afin de progresser. Vous devriez alors vous améliorer dans ces matières.
Bien à vous
Bonjour superProf !!!
Je vous remercie grandement pour cette page. J’ai toujours aimé les mathématiques même si elles ne sont pas du tout faciles… Mais je crois qu’avec vos conseils, je serai encore plus excellent
Bonjour,
Merci pour commentaire ! Et nous vous souhaitons toute la réussite en mathématiques.
Bien à vous
Bonjour je m’appelle armelia je suis en terminale D et je suis vraiment nul j’ai vraiment besoin de vos conseille pour m’aider a reussir mon bac et a être vraiment bonne en math
Bonjour,
Toutes les astuces sont déjà dans notre article. Vous pouvez également faire appel à un professeur de maths particulier pour vous aider dans vos devoirs et dans l’apprentissage de vos leçons.
Bien à vous
Bonsoir super prof mon problème c’est que j’aime beaucoup les mathématiques physiques et chimies j’arrive pas à traiter mes exercices je compurends rien je me bloque et pourtant je fais la 11 science
Bonjour,
Je vous conseille de revoir les exercices que vous avez eu du mal à réaliser et d’essayer de les refaire jusqu’à ce que vous compreniez le fonctionnement. Vous pouvez ensuite en faire d’autres via des annales ou des manuels de mathématiques pour vous entraîner.
Bon courage
Salut je m’appelle Diarra Gaoussou, je suis en classe de seconde (série scientifique). mon problème est que , quand j’étais dans les classe de 1er sicle. j’étais toujours 1er en maths, les exercices que je traitais je m’en sortais, aux devoirs comme à l’interrogation j’avais plus de points que toute la classe. mais arrivé 2nde je ne sais pas ce qui m’arrive. au cours je comprend et je traite les exercices, mais aux devoirs ou à l’interrogation je m’en sort pas trop et ça fait que j’ai failli ne pas trouver la moyenne. Je ne sais pas ce qui m’arrive. si vous pouvez m’aider en m’en sortir!
Bonjour,
Je vous conseille de reprendre les exercices des devoirs et de les refaire afin de comprendre ce que vous n’avez pas réussi à faire. De la sorte, vous pourrez être plus attentif et surtout plus préparé pour les prochains devoirs. Vous pouvez également faire appel à un prof particulier si besoin.
Bien à vous
Merci
Merci beaucoup pour votre article sa été pour moi une grande source d’expiration enfin d’apprendre les maths.
Bonjour,
Merci pour votre commentaire.
Bien à vous
J’ai des lacunes en mathématiques , je ne sais pas comment pourriez vous m’aider svp ?
Bonjour,
Vous avez de nombreuses astuces dans cet article. Vous pouvez également faire appel à un professeur particulier.
Bien à vous
tres interressant je veux reprendre mes cours merci
très intéressant
Bonsoir superprof , j’suis en première scientifique (PC ) j’aimerais vraiment avoir de très bonne note en math et en physique chimie mais je n’y arrive pas ,vraiment s’il vous plaît pouvez vous m’aider ???
Bonjour,
Il ne faut pas hésiter à refaire les exercices chez soi afin de bien les comprendre, surtout ceux sur lesquels vous avez faits des fautes. Se faire accompagner par un professeur est également l’idéal pour progresser rapidement.
Bien à vous
Merci beaucoup
Merci pour votre aide
bonjour, je veux savoir quelques jeux éducatifs afin d’améliorer mon niveau en maths et merci
Salut je cherche un sujet de mémoire sur les thèmes :problématique du raisonnement et de la logique dans l’enseignement des mathématiques ,problématique de l’évaluation en mathématique.
Boujour je suis Khady Mané Diouf au Sénégal suis en classe de seconde s et je vous remercie pour votre aide cordialement merci merci merci
Merci à vous Khady ! À bientôt ! :)
Bonjour je m’appelle innocent kensley je besoin évoluer en maths mais c’est impossible
Bonjour,
N’hésitez pas à prendre des cours particuliers avec Superprof.
Bien à vous
Bonjour parier a moi Aussi
bonjour je m’appelle Marie Grâce je suis étudiante en génie logiciel j’ai eu un baccalauréat A4 ou mes matières de base était philosophie littérature anglais espagnol. enffet je suis en première année dans le faculté de génie logiciel ou les mathématiques sont la base et j’ai pas de base en mathématiques je comprends rien je voudrais savoir comment faire pour mieux comprendre les mathématiques et aussi toute les matières scientifiques que je vais faire au courant de mes étude
Merci beaucoup pour ses astuces superprof . Et j’espère que tous cela vont vraiment m’aider parce que j’ai quelques difficultés à m’adapter sur les maths
La mathématiques, pour sa maîtrise c’est la répétition et la résolution des exos !!!
Bonjour mon nom c’est Marien BOZU je n’arrive pas à développer de la réponse, je comprends bien le cours de la mathématiques Au moment de sa explication mais on arrivant seul les tout est partie, comment dois je, pour avoir de bonnes mémoire de d’enregistrer et travailler seul.
Bonjour Marien,
C’est un problème courant en maths ! Pour mieux mémoriser et travailler seul, essayez de prendre des notes claires, de résumer chaque cours avec vos propres mots et de vous entraîner régulièrement avec des exercices. Expliquez aussi les notions à voix haute comme si vous les enseigniez, cela aide à mieux les retenir.
Avec Superprof, vous pouvez aussi prendre des cours particuliers pour revoir les points difficiles et progresser plus efficacement. Bonne journée !
Cool, merci pour tout
Très édifiant !
Peut-,on une version Pdf à telécharger ?
Merci!
Très bien
Je suis un élève de 3éme qui veux réussir son examen mais j’ai beaucoup de difficulté avec certains matiéres
C’est bon c’est très intéressant de faire comprendre aux autres ce qu’ils ignorent. Cet mérite qu’il soit porté à l’attention des apprenants, des enseignants et des parents d’élèves.
J’ai aimé et apprécié.Ceci fera des apprenants désireux de devenir bon en Maths