Chapitres
La loi de Wien, formulée par le physicien Wilhelm Wien, établit que la longueur d'onde du pic d'émission du rayonnement thermique émis par un corps est inversement proportionnelle à sa température.
? En d'autres termes, plus un corps est chaud, plus le pic d'émission se situe à des longueurs d'onde plus courtes
? Cette loi est fondamentale en physique et trouve des applications importantes dans de nombreux domaines, notamment en astronomie :
- Les astronomes l'utilisent pour déterminer la température des étoiles en analysant leur rayonnement thermique
- Grâce à cette loi, ils peuvent associer la couleur des étoiles à leur température, permettant ainsi d'obtenir des informations cruciales sur leur nature, leur taille, leur âge et leur évolution dans l'univers.
Vous voulez en savoir plus ? Consultez notre article ?

Comprendre la lumière et longueurs d'ondes ?

? La lumière, phénomène fascinant et omniprésent dans notre vie quotidienne, est une forme d'énergie électromagnétique qui se propage dans l'espace sous forme d'ondes. Ces ondes électromagnétiques sont constituées d'un champ électrique oscillant perpendiculairement à un champ magnétique.
⚡️ Elles voyagent à une vitesse constante de près de 300 000 kilomètres par seconde, soit la vitesse de la lumière
Une caractéristique essentielle de la lumière est sa capacité à se comporter comme une onde électromagnétique. Cela signifie que la lumière peut subir des phénomènes typiques des ondes, tels que :
La réfraction
La diffraction
L'interférence
Ces propriétés rendent la lumière particulièrement intéressante pour comprendre le fonctionnement de notre univers.
Longueur d'ondes et rôle pour la lumière visible
La longueur d'onde, qui joue un rôle crucial dans la composition de la lumière visible, est la distance entre deux crêtes successives d'une onde.
? Dans le cas de la lumière visible, la longueur d'onde se situe généralement dans une fourchette allant d'environ 400 à 700 nanomètres
? À retenir :
- Les longueurs d'onde plus courtes se trouvent dans la partie violette du spectre visible
- Les plus longues correspondent à la partie rouge
- Les autres couleurs de l'arc-en-ciel se placent entre ces extrémités
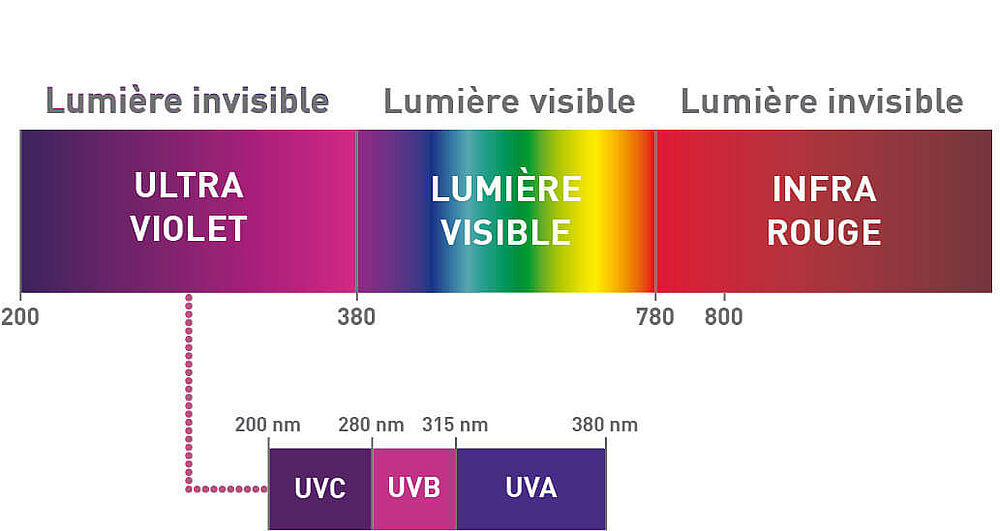
? Les longueurs d'onde sont étroitement liées à la perception des couleurs par l'œil humain. Par exemple, lorsque la lumière du soleil traverse des gouttelettes d'eau en suspension dans l'atmosphère, elle subit une dispersion, séparant la lumière en différentes longueurs d'onde. Le résultat est un magnifique arc-en-ciel, où chaque couleur est associée à une longueur d'onde spécifique.
? Outre l'arc-en-ciel, il existe de nombreux autres phénomènes optiques liés aux longueurs d'onde de la lumière :
- La diffraction se produit lorsque la lumière rencontre un obstacle ou une ouverture de taille similaire à sa longueur d'onde
- Cela peut provoquer des motifs d'interférences lumineuses spectaculaires, comme ceux observés dans des expériences impliquant des fentes d'Young
Grâce à la compréhension de ces propriétés, nous sommes en mesure d'expliquer une multitude de phénomènes optiques, et cela constitue également la base de nombreux autres domaines scientifiques tels que l'astronomie, la spectroscopie et bien d'autres encore.
Identifier la température d'un corps et le rayonnement thermique ?️

Température et rayonnement thermique
?️ La température d'un corps est une mesure de l'agitation thermique de ses particules constitutives. Plus précisément, elle représente la moyenne de l'énergie cinétique des molécules qui le composent :
Lorsqu'un corps possède une température élevée, cela signifie que ses particules sont très agitées et se déplacent rapidement
Tandis qu'un corps à basse température aura des particules moins agitées, se déplaçant plus lentement.
Le concept de rayonnement thermique est étroitement lié à la température d'un corps. Tout corps, quelle que soit sa température, émet du rayonnement électromagnétique sous forme de photons.
☢️ Ce rayonnement est appelé rayonnement thermique
Contrairement à la lumière visible que nous pouvons voir, le rayonnement thermique émis par des corps à des températures ambiantes est principalement situé dans la région infrarouge du spectre électromagnétique.
Rayonnement thermique et conséquences
Le rayonnement thermique est le résultat direct de l'agitation thermique des particules du corps. Lorsque ces particules vibrent et se déplacent, elles émettent des photons en raison de leurs interactions électromagnétiques. La quantité et la distribution de ce rayonnement dépendent de la température du corps.
? Un corps chaud émettra plus d'énergie et des photons de plus haute énergie qu'un corps froid
? La compréhension du rayonnement thermique et de son spectre a des applications importantes dans divers domaines scientifiques et technologiques. Dans les technologies thermiques, la détection de rayonnement infrarouge est utilisée dans les appareils de vision nocturne, les dispositifs de détection de chaleur, et même dans les télécommandes.
Expression de la loi de Wien : lien entre lumière et température ✏️

La loi de Wien, formulée par le physicien allemand Wilhelm Wien à la fin du 19e siècle, est une relation fondamentale en physique qui lie la longueur d'onde du pic d'émission d'un rayonnement thermique à la température du corps émetteur.
✍? Cette loi joue un rôle essentiel dans notre compréhension du rayonnement thermique et a des applications importantes dans de nombreux domaines, y compris en astronomie et dans les technologies de détection thermique
De manière simple, la loi de Wien peut être exprimée comme suit :
"La longueur d'onde du pic d'émission du rayonnement thermique est inversement proportionnelle à la température du corps"
Larousse
Cela signifie que plus un corps est chaud, plus la longueur d'onde à laquelle il émet le plus d'énergie est courte. Ainsi :
- Les objets chauds émettent principalement des rayonnements à des longueurs d'onde plus courtes, généralement dans le domaine du spectre visible ou même dans l'ultraviolet
- En revanche, les objets plus froids émettent principalement des rayonnements à des longueurs d'onde plus longues, qui se situent généralement dans l'infrarouge.
L'application de la loi aux sources chaudes
La loi de Wien s'applique aux sources chaudes (aussi appelées corps noirs) et permet de relier la température T d'une source chaude à la longueur d'onde de l'intensité lumineuse maximale λmax
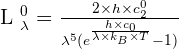
Le résultat de cette formule est exprimé en W.m-2.m-1.sr-1. Une fois simplifiée, avec la constante de Boltzmann kB égale à 1,38064852 x 10-23 J.K-1, c0 la vitesse de la lumière dans le vide (approximativement 3,00 x 108 m.s-1) et h la constante de Planck (6,62607004 x 10-34 m2.kg/s), on obtient la loi de Wien précédemment évoquée.
La loi peut alors s'écrire sous forme de la formule suivante :
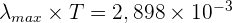
Dans cette formule :
- λmax est en mètre (m)
- T est en Kelvin (K)
- La constante 2,898 x 10-3 est exprimée en Kelvin mètre (K.m)
- La loi arrondie correspond alors à une luminescence maximale égale à :
Le Kelvin
? Dans la loi de Wien, la température s'exprime en kelvin (K). C’est cette unité qui permet de mesurer la température dans le système international de mesure (SI). Le Kelvin permet une mesure absolue de la température. C’est à l’aide de cette unité que l’on peut mesurer le zéro absolu, température la plus basse qui puisse exister sur Terre.
Elle correspond à 0 K, soit – 273,15 °C
Si θ est la température exprimée en degrés Celsius et T la température exprimée en Kelvin, alors la relation entre les deux est :
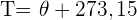
? Il est important de noter qu’on ne parle pas de « degré Kelvin », mais bien de Kelvin
Exemple d'application concrète
?Supposons que nous chauffions une plaque métallique à une température relativement basse, par exemple, 500 degrés Celsius (°C).
- En utilisant un spectromètre, nous mesurerions le rayonnement émis par la plaque et tracerions un graphique représentant l'intensité du rayonnement en fonction de la longueur d'onde. Nous constaterions que le pic d'émission se situe dans la région de l'infrarouge.
- Ensuite, si nous augmentons la température de la plaque à 1000 °C, nous observerions une augmentation de l'intensité du rayonnement émis dans l'infrarouge, et un déplacement du pic d'émission vers des longueurs d'onde plus courtes, se rapprochant du spectre visible.
- Enfin, en chauffant la plaque à une température extrêmement élevée, par exemple 5000 °C, nous verrions une nette augmentation de l'intensité du rayonnement émis dans le domaine du spectre visible, avec un pic d'émission maintenant dans la partie du bleu ou de l'ultraviolet.
Utilisation de la loi de Wien en astronomie ?

La loi de Wien peut être utilisée pour déterminer la température d'une source chaude dont le spectre et λmax sont connus, ou inversement il est possible de déterminer λmax à partir de la température d'une source chaude.
Mesure de la température des étoiles
? Dans l'astronomie, la loi de Wien joue un rôle crucial dans la détermination de la température des étoiles. Les astronomes utilisent le rayonnement thermique émis par les étoiles pour en déduire leur température de surface, ce qui permet de mieux comprendre leur nature et leur évolution.
Pour cela, il suffit d’observer le spectre d’une étoile donnée, et de déterminer la longueur d’onde pour laquelle on obtient un maximum d’intensité lumineuse (aussi appelé « luminance spectrale »).
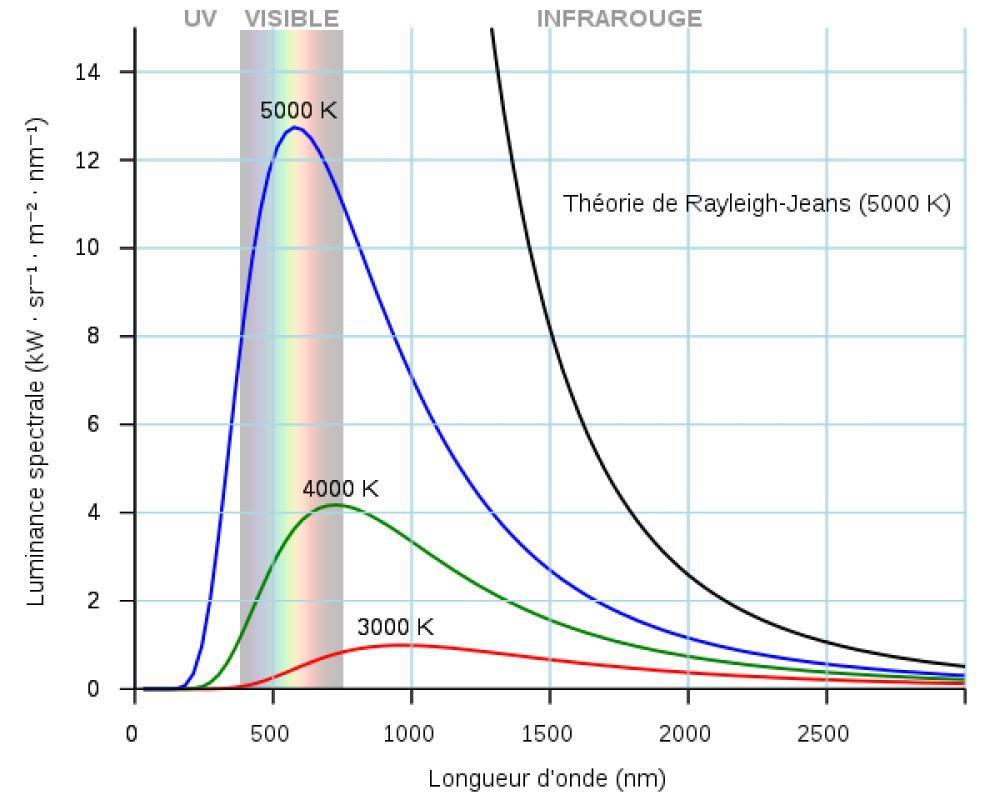
☄️ On applique alors la loi de Wien, qui permet de déterminer la température de l’étoile. La loi de Wien permet d’expliquer que les étoiles rouges sont beaucoup moins chaudes que les étoiles bleues. La loi de Wien permet de réaliser une classification des étoiles selon leurs types spectraux, qui correspondent chacun à une température de surface caractéristique. La couleur des étoiles est ainsi étroitement liée à leur température.
En utilisant le diagramme de Hertzsprung-Russell (HR), les astronomes peuvent visualiser cette relation. Le diagramme HR est un graphique qui représente la luminosité des étoiles en fonction de leur température de surface.
| Classe | Température | Longueur d'onde maximale | Couleur | Raies d'absorption |
|---|---|---|---|---|
| O | 60 000 - 30 000 K | 100 nm | Bleue | N, C, He et O |
| B | 30 000 - 10 000 K | 150 nm | Bleue-blanche | He et H |
| A | 10 000 - 7 500 K | 300 nm | Blanche | H |
| F | 7 500 - 6 000 K | 400 nm | Jaune - blanche | Métaux : Fe, Ti, Ca et Mg |
| G | 6 000 - 5 000 K | 500 nm | Jaune (similaire au Soleil) | Ca, He, H et métaux |
| K | 5 000 - 3 500 K | 750 nm | Jaune-orangée | Métaux et oxyde de titane |
| M | 3 500 - 2 000 K | 1000 nm | Rouge | Métaux et oxyde de titane |
Un simple moyen mnémotechnique afin de mémoriser ces classes serait :
« Oh, Be A Fine Girl Kiss Me ».
? Ainsi, on constate :
Les étoiles chaudes, ayant des températures élevées, sont situées dans la partie supérieure du diagramme HR. Elles émettent principalement une lumière bleue ou bleu-blanc. Les étoiles bleues sont généralement très brillantes et massives. Par exemple, les étoiles de type O et B sont classées comme des étoiles chaudes.
En revanche, les étoiles froides, avec des températures plus basses, se trouvent dans la partie inférieure du diagramme HR. Elles émettent principalement une lumière rouge ou rougeâtre. Les étoiles rouges sont souvent moins brillantes et moins massives. Les étoiles de type M sont un exemple d'étoiles froides.
✨ Un exemple d'étoile chaude serait Sirius, l'étoile la plus brillante du ciel nocturne, qui brille d'un éclat bleu-blanc évident.
? À l'inverse, Betelgeuse, une supergéante rouge dans la constellation d'Orion, est un exemple d'étoile froide qui affiche une couleur rougeâtre caractéristique.
Mesures courantes
De la même façon, on peut déterminer la température d’une source chaude à courte distante à l’aide d’un spectromètre. Il est cependant nécessaire de garder à l’esprit que la lumière provenant d’un objet n’est pas nécessairement de nature thermique : couleur et température ne sont pas toujours liés. En effet, si on suivait strictement la loi de Wien en calculant la « température du ciel » avec une longueur d’onde maximale de 400 nm, on obtiendrait une température de 7200°C !
? En conclusion, la loi de Wien est un outil fondamental dans l'astronomie qui permet aux astronomes de déterminer la température des étoiles en analysant leur rayonnement thermique. En utilisant le diagramme de Hertzsprung-Russell, les astronomes peuvent également établir un lien entre la couleur des étoiles et leur température de surface, ce qui offre des informations essentielles sur la nature et l'évolution de ces astres fascinants dans l'univers.
























Si vous désirez une aide personnalisée, contactez dès maintenant l’un de nos professeurs !
Bonjour j ai suivi et j ai compris relation entre temperature et longueur d onde mais a la fin la couleur du ciel et la temperature je me suis egaré merci
Bonjour merci pour votre commentaire! Si vous souhaitez un soutien sur un cours de physique-chimie, n’hésitez pas à solliciter un professeur :)
Beau article
Quelle est la fonction qui donne la courbe d’une 🔯🌟 étoile ?c’est une caractéristique de la neurone etoilée.Alors félicitations et bienvenue encouragements tendent vers notre haute études universitaires
Bonjour, je suis élève de 1ere et j’ai un soucis, je sais que c’est pas vraiment l’endroit approprié mais.. J’ai une question « à l’aide de la loi de wien, expliquer pourquoi le sol émet majoritairement des infrarouges? »
Bonjour, nos talentueux professeurs sont disponibles pour toute aide personnalisée, n’hésitez pas à les solliciter 🙂
Oui, en tout cas c’est clair que c’est fait uniquement pour des hommes, qui ont la capacité de raisonner. Moi en tant que fille je ne comprends rien lol
EH ! Consoeur ! Il est où le féminisme ???!!!
Bonjour,
Contrairement à ce que certaines personnes peuvent penser, les filles n’ont pas une capacité à raisonner moindre que les hommes. Pour preuve, nombreux sont nos rédacteurs qui sont en réalité… Des rédactrices !
Je vous invite alors à poser toutes les questions qui vous permettront de mieux comprendre les notions qui vous sont floues.
C’est vrai que votre cours es trés bien fait