Chapitres
L'effet Doppler est un phénomène physique qui a été découvert par Christian Doppler en 1842. Doppler était un physicien autrichien qui étudiait la lumière et le son. L'effet Doppler est également connu sous le nom de décalage Doppler et il décrit comment la fréquence d'une onde change en fonction de la position relative de la source de l'onde et de l'observateur.
Lorsque la source de l'onde s'approche de l'observateur, la fréquence de l'onde semble augmenter et lorsque la source s'éloigne de l'observateur, la fréquence de l'onde semble diminuer. Cela peut être observé avec la lumière, le son et même les ondes radio.
L'effet Doppler est utilisé dans de nombreux domaines, notamment en astronomie pour déterminer la vitesse de déplacement des étoiles et des galaxies. Il est également utilisé dans la médecine pour mesurer la vitesse du flux sanguin et dans les radars pour détecter la vitesse des objets.
En résumé, l'effet Doppler est un phénomène très intéressant qui a été découvert il y a plus de 150 ans et qui est utilisé dans de nombreux domaines pour mesurer la vitesse de déplacement des objets.

Lorsque l'ambulance s'approche de l'observateur, la fréquence perçue du son augmente, ce qui rend la sirène plus aiguë. Lorsque l'ambulance s'éloigne de l'observateur, la fréquence perçue diminue, ce qui rend la sirène plus grave.
Ce phénomène est utilisé dans la vie quotidienne pour alerter les gens de l'arrivée imminente d'une ambulance ou d'un véhicule d'urgence.
Christian Doppler
Christian Doppler était un physicien autrichien né en 1803 et mort en 1853. Il a étudié la lumière et le son et est célèbre pour avoir découvert l'effet Doppler en 1842. Cet effet décrit comment la fréquence perçue d'une onde change en fonction de la position relative de la source de l'onde et de l'observateur.
Christian Doppler a également travaillé sur d'autres sujets scientifiques, notamment la réfraction de la lumière, l'élasticité des corps et la théorie de la chaleur. Sa contribution à la physique et à la science en général est considérée comme importante et a influencé de nombreux scientifiques qui ont suivi ses pas.

Fréquence d'une onde émise par une source en mouvement
Si une source en mouvement de vitesse Vs émet une onde de fréquence f, de période T et de longueur d'onde λ qui se propage à une célérité c vers un un observateur immobile alors, à cause de l'effet Doppler, ce dernier perçoit une onde de fréquence fe, de période Te et de longueur d'onde λe. Dans le cas général où la source se déplace, l'effet Doppler est défini par la formule suivante :
f' = f * (v ± vd) / (v ± vs)
où :
- f' est la fréquence observée
- f est la fréquence émise par la source
- v est la vitesse de propagation de l'onde
- vd est la vitesse relative de la source par rapport à l'observateur
- vs est la vitesse relative de l'observateur par rapport à la source
Le signe ± dépend de la direction du mouvement relatif entre la source et l'observateur. Si la source s'approche de l'observateur, le signe est négatif. Si la source s'éloigne de l'observateur, le signe est positif.
Un rapprochement source/récepteur cause une augmentation de la fréquence, on remplacera donc les signe de la formule par un "+". Un éloignement source/récepteur cause une diminution de la fréquence.
Utilisation de l'effet Doppler pour mesurer une vitesse
L'effet Doppler peut être utilisé pour déterminer la vitesse d'un objet en mouvement relatif par rapport à un observateur. Pour cela, il faut mesurer la différence de fréquence entre la fréquence émise par la source et la fréquence observée par l'observateur.
La formule de l'effet Doppler peut être utilisée pour calculer cette différence de fréquence. En connaissant la vitesse de propagation de l'onde, ainsi que les vitesses relatives de la source et de l'observateur, on peut déterminer la fréquence observée et la fréquence émise par la source. Ensuite, en utilisant la formule de l'effet Doppler, on peut résoudre pour la vitesse relative.
Il est important de noter que l'effet Doppler ne peut mesurer que la vitesse relative entre la source et l'observateur. Si la vitesse de propagation de l'onde est inconnue, il peut être difficile de déterminer la vitesse absolue de l'objet en mouvement.

Nous reviendrons plus en détail sur ce point plus bas dans l'article.
Applications de l'effet Doppler
Echographie Doppler
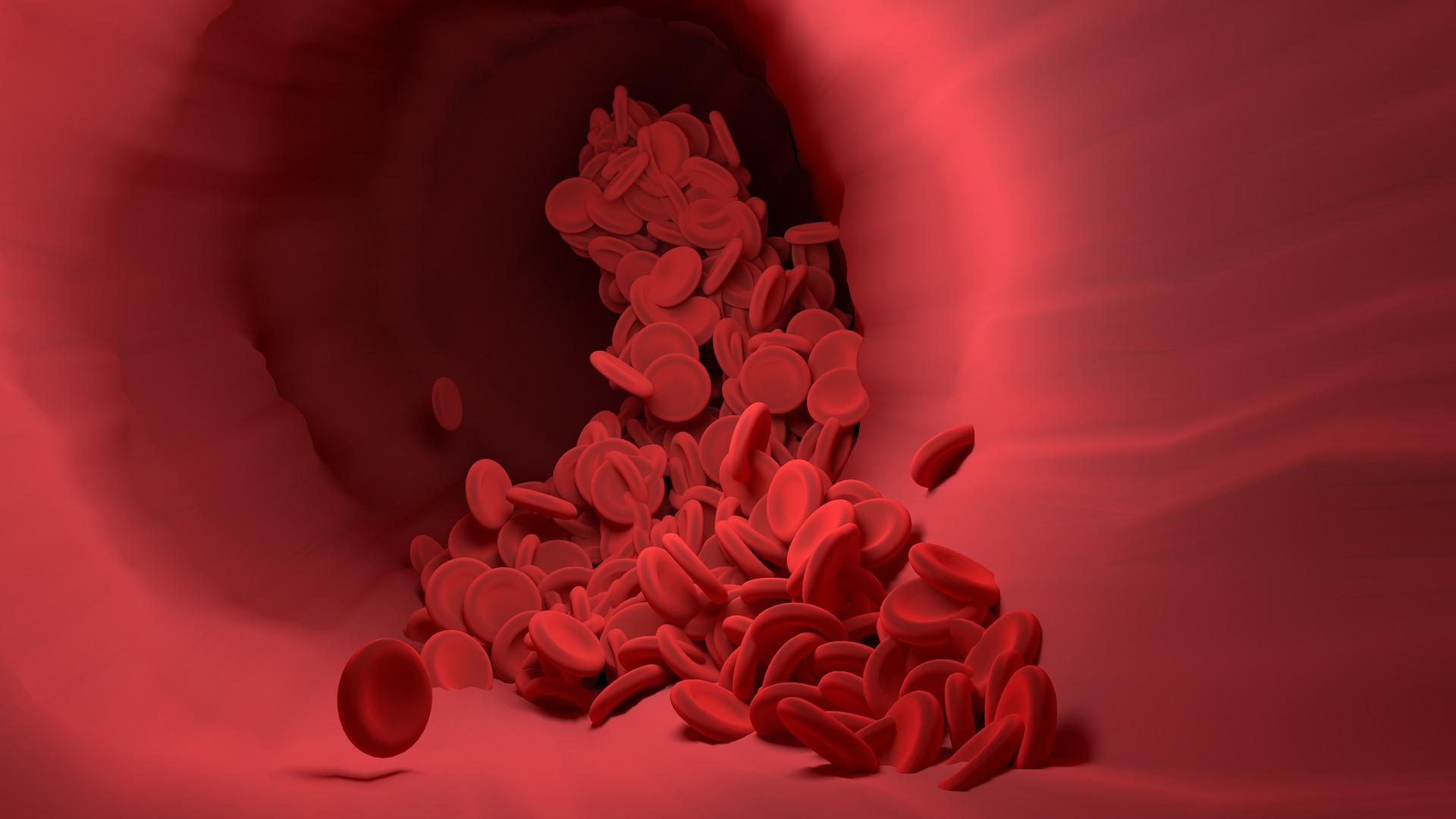
L'échographie Doppler est une technique d'imagerie médicale qui utilise l'effet Doppler pour visualiser la circulation sanguine. Elle mesure la variation de la fréquence d'une onde ultrasonore réfléchie par les globules rouges en mouvement dans les vaisseaux sanguins.
Lorsqu'un faisceau d'ultrasons est envoyé vers les tissus corporels, une partie des ondes est réfléchie par les globules rouges en mouvement. Cette réflexion est appelée l'effet Doppler. La fréquence de l'onde réfléchie est différente de la fréquence de l'onde émise en raison du mouvement des globules rouges.
L'échographie Doppler utilise cette différence de fréquence pour déterminer la direction et la vitesse du flux sanguin. Les informations sont traitées par un ordinateur et visualisées sous forme d'images en temps réel qui montrent la direction et la vitesse du flux sanguin.
L'échographie Doppler est souvent utilisée pour diagnostiquer des problèmes circulatoires, tels que des caillots sanguins, des varices ou des malformations vasculaires. Elle peut également être utilisée pour évaluer la circulation sanguine dans le cœur, les reins et d'autres organes.
Le contrôle de vitesse par radar
Les radars sont des dispositifs électroniques utilisés pour détecter la présence, la position et la vitesse d'objets. Le principe de fonctionnement des radars repose sur l'émission d'ondes électromagnétiques qui se propagent dans l'espace et qui sont réfléchies par les objets rencontrés sur leur chemin. Les ondes réfléchies sont alors captées par le radar qui les analyse pour déterminer les caractéristiques de l'objet rencontré.
Les radars utilisent l'effet Doppler pour mesurer la vitesse de déplacement des objets en mouvement. Les ondes radio émises par le radar sont réfléchies par l'objet en mouvement et la fréquence de ces ondes est modifiée en fonction de la vitesse de l'objet. Si l'objet se déplace vers le radar, la fréquence des ondes réfléchies sera plus élevée que la fréquence des ondes envoyées. Si l'objet s'éloigne du radar, la fréquence des ondes réfléchies sera plus basse que la fréquence des ondes envoyées. En mesurant la différence de fréquence entre les ondes envoyées et réfléchies, il est possible de déterminer la vitesse de déplacement de l'objet.
L'utilisation de l'effet Doppler dans les radars est très répandue, notamment dans les domaines de la météorologie, de l'aviation, de la navigation maritime et de la défense. Les contrôles radar permettent de mesurer la vitesse des avions, des bateaux et des véhicules terrestres, ainsi que de détecter la présence de précipitations et d'autres phénomènes météorologiques. Les radars sont également utilisés pour surveiller les mouvements de troupes et de véhicules ennemis sur les champs de bataille.
En résumé, l'utilisation de l'effet Doppler dans les radars est un exemple concret de la manière dont la physique peut être appliquée dans des domaines pratiques pour répondre à des besoins spécifiques. Les contrôles radar sont un élément important de la surveillance de la circulation aérienne et maritime, ainsi que dans les opérations militaires.
Analyse du mouvement des étoiles
L'analyse du mouvement des étoiles par effet Doppler est un domaine important de l'astronomie. En utilisant l'effet Doppler pour mesurer les changements de fréquence de la lumière émise par des étoiles, les astronomes peuvent déterminer si une étoile se rapproche ou s'éloigne de la Terre, ainsi que sa vitesse relative. Cela permet également de détecter les étoiles qui tournent autour d'un centre de masse commun, comme dans les systèmes binaires d'étoiles. L'analyse du mouvement des étoiles par effet Doppler a été utilisée pour découvrir de nouvelles planètes en dehors de notre système solaire en détectant les mouvements subtils des étoiles autour desquelles elles orbitent.
De plus, l'analyse du mouvement des étoiles par effet Doppler a également permis de découvrir des phénomènes tels que les naines blanches, les étoiles à neutrons et les trous noirs. En observant les changements de fréquence de la lumière émise par ces objets, les scientifiques peuvent déterminer leur masse, leur distance et leur vitesse de déplacement.
L'analyse du mouvement des étoiles par effet Doppler est une technique précieuse pour comprendre l'univers et découvrir de nouveaux phénomènes astrophysiques. Elle est utilisée dans de nombreux projets de recherche, tels que la recherche de planètes similaires à la Terre ou l'étude de la formation des galaxies.
Enfin, il est important de noter que l'effet Doppler est également utilisé dans d'autres domaines de l'astronomie. Par exemple, les astronomes peuvent utiliser l'effet Doppler pour mesurer la vitesse de rotation des galaxies. En observant la lumière émise par des étoiles situées à différentes distances du centre d'une galaxie, les astronomes peuvent déterminer la vitesse à laquelle la galaxie tourne. Cela permet de mieux comprendre la structure et l'évolution des galaxies.
L'effet Doppler est également important dans l'étude de la cosmologie, la branche de l'astronomie qui étudie l'origine, la structure et l'évolution de l'univers dans son ensemble. En observant la lumière émise par des galaxies lointaines, les astronomes peuvent utiliser l'effet Doppler pour mesurer la vitesse à laquelle ces galaxies s'éloignent de la Terre. Cela permet de déterminer la vitesse d'expansion de l'univers et d'étudier les théories sur son origine et son évolution.
En conclusion, l'effet Doppler est un phénomène physique important qui est utilisé dans de nombreux domaines de l'astronomie. De la détection de planètes en dehors de notre système solaire à l'étude de la structure de l'univers, l'effet Doppler nous permet de comprendre notre place dans l'univers et de découvrir de nouvelles merveilles astrophysiques.
L'effet Doppler-Fizeau est un phénomène similaire à l'effet Doppler, mais qui s'applique aux ondes lumineuses plutôt qu'aux ondes sonores ou radio. L'effet Doppler-Fizeau décrit comment la fréquence de la lumière change en fonction de la vitesse relative de la source de lumière et de l'observateur. L’effet Doppler-Fizeau a été découvert par Hippolyte Fizeau en 1848, seulement six ans après la découverte de l'effet Doppler par Christian Doppler. Fizeau était un physicien français qui a effectué de nombreuses recherches sur la lumière et la vitesse de la lumière.
L'effet Doppler-Fizeau est utilisé pour mesurer la vitesse de déplacement des étoiles et des galaxies dans l'univers. En observant le décalage de la fréquence de la lumière émise par une étoile ou une galaxie lointaine, les astronomes peuvent déterminer si elle s'approche ou s'éloigne de la Terre, ainsi que sa vitesse relative. Cela permet de mieux comprendre la structure et l'évolution de l'univers dans son ensemble.
L'effet Doppler-Fizeau est également utilisé dans d'autres domaines de l'astronomie, tels que la détection de supernovas et la mesure des distances dans l'univers. En utilisant l'effet Doppler-Fizeau, les astronomes peuvent déterminer la distance des étoiles et des galaxies en mesurant la quantité de décalage de la fréquence de la lumière émise par ces objets.
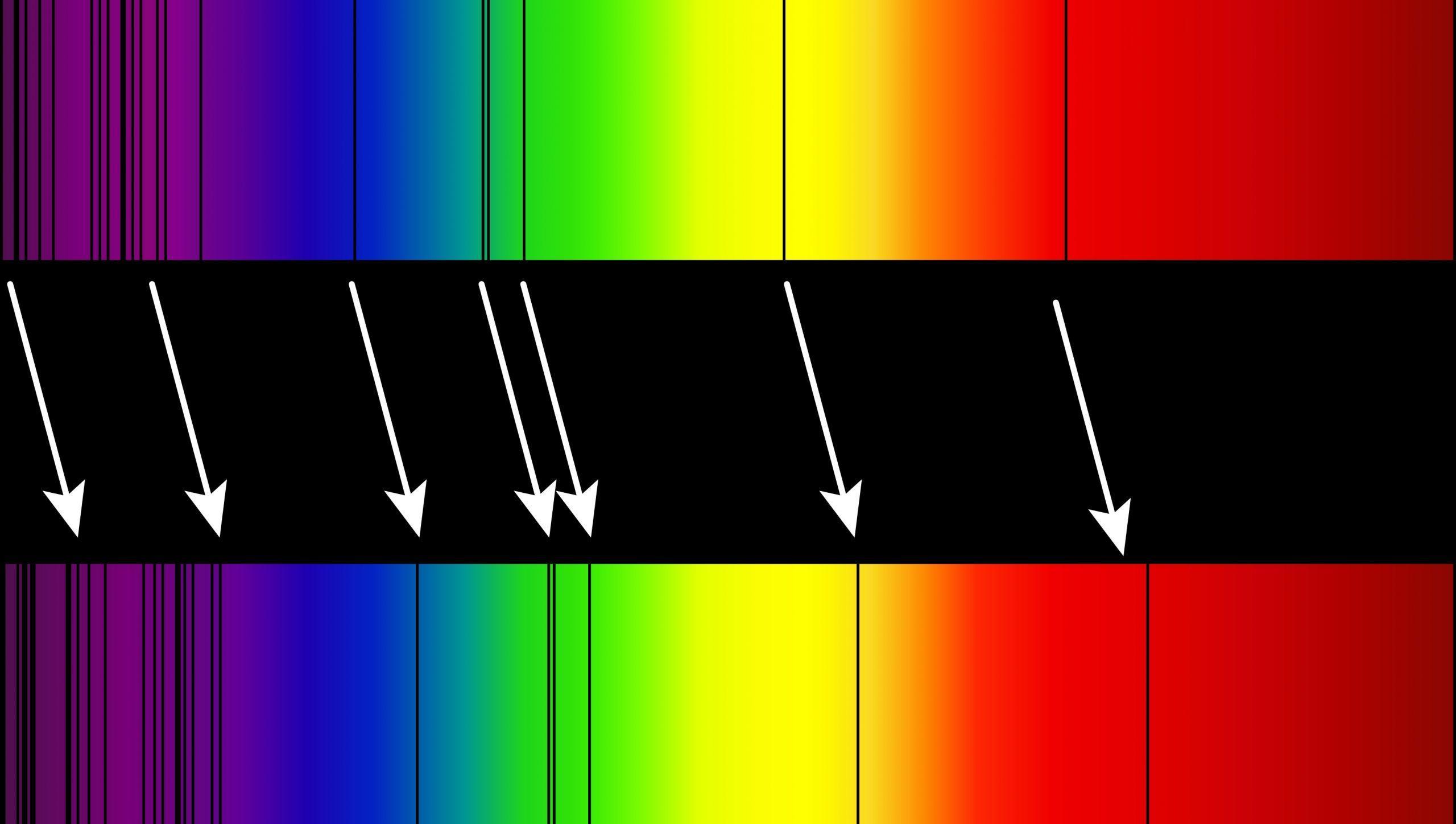
Dans le cas d'une étoile qui s'éloigne (notamment à cause de l'expansion de l'univers), les lumières de son spectre ont des longueurs d'onde plus grandes (d'autant plus que la vitesse est élevée) : on parle d'un décalage vers le rouge, aussi appelé "redshift". Plus ce déplacement est rapide, plus les raies sombres d'absorption de certains atomes du spectre des étoiles sont déplacées vers le rouge. Si une étoile s'approche, le phénomène inverse se produit : on observe alors un "blueshift". La loi de Hubble suppose un rapport constant entre la vitesse et l'éloignement d'une étoile, il est donc possible de connaitre la distance entre la Terre et l'étoile par la mesure de sa vitesse d'éloignement. Cette méthode permet également de détecter des exoplanètes (planètes hors du système solaire). Ces exoplanètes provoquent un mouvement périodique de toute étoile à proximité, mesurable à l'aide de l'effet Doppler, qui permet par la suite de déterminer la masse de la planète.
Loi de Hubble
La Loi de Hubble est une découverte fondamentale en astronomie qui a permis de mieux comprendre l'histoire et l'évolution de l'univers. Elle a été découverte par l'astronome Edwin Hubble en 1929, qui a observé que les galaxies les plus éloignées de la nôtre semblaient s'éloigner plus rapidement que les galaxies plus proches. Cette observation a conduit à la formulation de la théorie de l'expansion de l'univers, qui est aujourd'hui largement acceptée par les scientifiques.
Selon cette théorie, l'univers a commencé à se dilater à partir d'un point unique il y a environ 13,8 milliards d'années, lors du Big Bang. Depuis lors, l'univers s'est étendu et continue de s'étendre de manière homogène dans toutes les directions. La Loi de Hubble a permis aux scientifiques de mesurer cette expansion, ainsi que la vitesse à laquelle les galaxies s'éloignent les unes des autres.
La Loi de Hubble peut être décrite mathématiquement par l'équation de Hubble, qui relie la vitesse de récession d'une galaxie à sa distance de la Terre. Cette équation montre que plus une galaxie est éloignée de la nôtre, plus elle s'éloigne rapidement. Cette observation a également permis aux scientifiques de déterminer l'âge de l'univers et de mieux comprendre sa structure.
L'expansion de l'univers a également permis aux scientifiques de formuler des hypothèses sur son sort ultime. Selon la théorie de l'univers en expansion, l'univers continuera de s'étendre indéfiniment. Cependant, il y a également la possibilité que l'expansion ralentisse à un moment donné et que l'univers commence à se contracter de nouveau, conduisant à un Big Crunch.
La navigation des chauve-souris
Les chauves-souris sont des mammifères volants qui ont développé une capacité extraordinaire pour chasser leurs proies dans l'obscurité. Elles utilisent un système de navigation sonore appelé écholocation pour détecter les objets qui les entourent et pour se diriger dans l'obscurité. Plus précisément, les chauves-souris émettent des sons à haute fréquence qui rebondissent sur les objets environnants, puis elles écoutent les échos qui leur reviennent. En mesurant la fréquence de ces échos, les chauves-souris peuvent déterminer la position et la vitesse de leurs proies.
L'effet Doppler est une partie importante de la capacité des chauves-souris à chasser leurs proies. Comme les proies se déplacent, la fréquence des échos change en fonction de l'effet Doppler. Si la proie se déplace vers la chauve-souris, la fréquence des échos est plus élevée que la fréquence des sons émis. Si la proie s'éloigne, la fréquence des échos est plus basse que la fréquence des sons émis. En mesurant cette différence de fréquence, les chauves-souris peuvent suivre les mouvements de leurs proies et les attraper.

L'écholocation est une capacité essentielle pour la survie des chauves-souris dans leur environnement nocturne. Les chauves-souris chassent principalement des insectes, qui sont en mouvement constant et très difficiles à repérer dans l'obscurité. Grâce à leur système d'écholocation et à l'effet Doppler, les chauves-souris sont capables de repérer et de suivre leurs proies avec une grande précision.
L'étude de l'écholocation chez les chauves-souris a également des implications pour la technologie humaine. Les scientifiques ont étudié le système d'écholocation des chauves-souris pour concevoir des systèmes de radar et de sonar plus efficaces. De plus, les chauves-souris ont inspiré la conception de drones qui utilisent des capteurs acoustiques pour naviguer dans l'obscurité.
Résumer avec l'IA :























Si vous désirez une aide personnalisée, contactez dès maintenant l’un de nos professeurs !
Super cours ! Sybille Gros à adoré et elle vous fait de gros bisous 🥰🥰
je vous remercie infiniment
quelle sont les metaux qui peut absorber les onde du radar (onde radio)?
Bonjour, il nous ferait plaisir de vous aider, n’hésitez pas à contacter nos professeurs sur la plateforme de Superprof. :)
Bonjour, merci beaucoup bonne soiré les couz du 12
Bonjour et merci pour cet article très intéressant. J’aurai une question sur un cas particulier. Si Vs = c, que devient fe ? L’expression n’est pas définie pour ce cas quand la source se rapproche. Or c’est le cas de l’avion qui se rapproche en étant à la vitesse du son. Ce problème n’apparait qu’à cette vitesse et ce pour un objet se rapprochant uniquement. Comment pourrait-on l’interpréter?
Merci d’avance,
Comment je peux faire une expérience facile pour monter comment ce radar fonctionne
Bonjour Hasna,
Une expérience simple à mettre en oeuvre pour montrer l’effet Doppler est celle du diapason.
Fixez l’extrémité d’un diapason à une corde. Faites-le vibrer ou allumez-le s’il s’agit d’un diapason électrique.
Une fois qu’il vibre, faites-le tourner au dessus de votre tête en prenant garde de ne heurter rien ni personne.
Vous entendrez bien les différences de fréquences qui montrent les effets de l’effet Doppler.
Bonne journée
Bonjour,
Des ondes destructives se produisent lors de la présence d’interférences destructives. Par exemple, lorsque les ondes à la surface d’un plan d’eau se rencontrent.
Bonne journée