Chapitres

Rappel : mole et quantité de matière

La mole est une unité de quantité de matière.
La quantité de matière se note n et s'exprime en mole de symbole mol.
Le nombre d'entités élémentaire contenue dans une mole est appelé Constante d'Avogadro, noté Na.
Il faut savoir que la valeur du nombre d'Avogadro a évolué au court du temps :
- Avant le 20 Mai 2019, le nombre d'Avogadro, et donc la mole, était défini comme correspondant au nombre d'atome de carbone dans 12 grammes (donc 10-3 kg) de carbone 12. On avait alors : NA = 6,022 140 857 . 1023 mol−1.
- Or, depuis le 20 Mai 2019, le kilogramme a été redéfini. Ainsi, on fit le choix de définir le nombre d'Avogadro comme étant une constante fixée par convention. Aujourd'hui, la valeur du nombre d'Avogadro est donc : NA = 6,022 140 76 . 1023 mol−1
Il y a proportionnalité entre le nombre N d'entités élémentaires dans un échantillon et sa quantité de matière n :
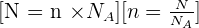
La masse

En physique, la masse correspond à une grandeur physique positive et intrinsèque d'un corps.
De façon plus précise, en physique newtonienne, la masse correspond à une grandeur extensive. Cela signifie alors que la masse d'un corps formé de parties correspond à la somme des masses de ces différentes parties qui le compose.
De plus, il est essentiel de noter que la masse est une grandeur conservative. De ce fait, elle reste constante dans le cas d'un système isolé qui n'échange donc pas de matière avec son environnement.
Pour une espèce donnée, la masse m, la quantité de matière n et la masse molaire M sont liés par : 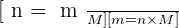
Les propriétés
La masse peut se manifester au travers de deux propriétés fondamentales :
En effet, en mécanique statique, la masse est correspond à l'un des premières grandeurs facilement mesurable par les gens via le système de pesée puisque celle-ci permet de comparer la masse de l'objet défini avec un masse étalon connue. On appellera alors ce système la masse pesante. C'est ainsi que l'on liera la quantité de matière d'un corps à sa masse.
Tandis qu'en mécanique dynamique, la masse correspond à une grandeur qui intervient dans le principe fondamental de la dynamique comme étant la résistance de la matière au changement de vitesse. En effet, plus la masse d'un corps est importante, plus il faudra exercer une force important pour modifier la direction ou encore sa vitesse. On appelle alors ce phénomène "masse inerte".
Ainsi, cet aspect de la masse présente un rôle essentiel dans tous les domaines de la dynamique puisqu'elle correspond à une notion présente dans grand nombre de relations de physique classique ou encore dans les calculs qui permettent de les définir. En effet, il est possible de constater une proportionnalité entre la masse inerte et la masse pesante et cela de façon totalement indépendante de la nature du matériau mis en jeu. Cela permet alors de prendre la même unité pour la masse pesante et la masse inerte et donc de pouvoir les définir comme étant égale. Ainsi, cette équivalence à permis de définir un principe d'équivalence.
Vous cherchez un cours de physique chimie 5ème ?
L'unité
L'unité de masse est le kilogramme dans le Système international d'unités (S.I.).
Comme pour le litre il existe des sous-unités : kg ; hg ; dag ; g ; dg ; cg ; mg .
Attention à ne pas faire comme une majorité et confondre la masse avec le poids. En effet, dans le vocabulaire de la physique, le poids correspond à la force exercée par la gravité sur un corps pesant.
La masse se mesure avec une balance

Balance de Roberval
C'est généralement avec cet outil qu'on vous a sensibilisé en école primaire à la notion de masse bien que, très souvent, les professeurs sèment la confusion en utilisant le terme de "poids" alors méfiez-vous de ce que vous pensez savoir !
La balance de Roberval à deux fléaux correspond à un instrument de pesage nommé ainsi en hommage à son inventeur qui n'est d'autre que Gilles Personne de Roberval, un célèbre mathématicien mais aussi physicien français né en 1602.
Petite anecdote amusante, ce scientifique est connu sous le nom de Roberval puisque celui-ci était originaire de Roberval dans l'Oise.
Le mathématicien Gille Personne a inventé cette balance lorsqu'il a eu l'idée de place des plateaux au dessus du fléau alors que, de façon traditionnelle, ces plateaux étaient suspendus en dessous du fléau. Ainsi, Le principe de l'énigme statique expliquant que les position des masses sur les plateaux ne perturbent pas le résultat final de la mesure, sera présenté sous la forme de thèse devant l'Académie royale des sciences par Gilles Personne de Roberval en 1669.
Balance électronique
Cette balance correspond à ce que vous trouverez certainement dans vos cuisines. Un plateau unique avec un écran indiquant la mesure avec une précision dépendant de l'appareil.
A noter que la balance la plus sensible au monde a vu le jour en 2012 par des chercheurs de l’Institut Catalan de Nanotechnologie. Celle-ci permet de peser au yoctogramme près.
La masse de l'objet dépend de la densité de l'objet mais également du volume
A noter que déclarer que 1 Litre pèse 1 Kilogramme est totalement faux. En effet, un litre d'huile pèse 800 g et non pas 1 kg.
Le Volume
On utilise le mètre cube de symbole m3.
On utilise plutôt le litre en chimie ( L ).
1 m3 = 1000 L et 1 mL = 1 cm3
La masse volumique d'un échantillon est le rapport de la masse m de cet échantillon à son volume v. ( p est la masse volumique )
p = m / v ou m = p x v ou v = m / p
La densité d'un liquide est égale au quotient de la masse d'un volume v par la masse d'un même volume d'eau. ( la densité s'exprime sans unité )
d = masse d'un volume v de liquide/ masse d'un volume v d'eau
Définition
Selon le domaine dans lequel ce mot est utilisé, la définition peut être différente. Mais, dans tout les cas, le volume représente une grandeur qui permet la mesure de l'extension d'un objet ou d'une partie de l'espace.
- En sciences physique, le volume d'un objet permet de mesurer l'extension dans l'espace physique que celui-ci possède et ce dans les trois direction de façon simultanée et de façon similaire à l'aire d'une figure dans le plan qui, quant à elle, mesure l'extension que celle-ci possède dans deux directions de façon simultanée.
- En mathématiques, le volume d'une partie de l'espace géométrique correspond à sa mesure dans le sens de la théorie de la mesure de Lebesgue.
Il peut être intéressant de connaître la notion de volume afin de déduire la masse d'un objet défini grâce notamment à la bien connue masse volumique !
Prélever un liquide
On verse directement le liquide dans le récipient gradué.
Attention : Il est important, lors d'une mesure, de placer son œil en bas du ménisque car la lecture du volume sur ce type de burette se fait au rétrécissement du trait bleu dû à un effet d'optique.
Mesurer le volume d'un solide
Dans le Système International d'Unités, le volume se mesure en mètre cube bien que le litre soit très fréquemment utilisé, notamment en ce qui concerne les liquides et autres matières sèches. De ce fait, on considère le volume comme étant une grandeur extensive dont la grandeur intensive thermodynamique associée est la pression.
Protocole
Méthode 1
Durant cette méthode, le solide correspond à un bouchon en liège ( = 15 mL ) mesuré avec une éprouvette graduée.
- Verser un liquide dans un récipient graduée .
- Noter le volume V1 ; V1 = 100ml .
- Ajouter l'objet de volume inconnu .
- Renoter le volume V2 ; V2 = 115 mL .
- Soustraire V1 à V2 .
V bouchon = V2 - V2 = 115 - 100 = 15 mL
Méthode 2
Avec une source de chaleur spéciale, on peut faire fondre l'objet. Il sera ensuite mesuré comme liquide.
Méthode 3
Par les mathématiques
Si on connaît la formule mathématique du volume de l'objet on peut l'appliquer .
Exemple : Un cube de côté de 5 cm :
V = 5 x 5 x 5 = c x c x c = 125 cm3
Les unités de volumes
Il existe deux unités de volume .
- Le litre de symbole L
- Le mètre cube de symbole m3
Il faut surtout retenir que 1 mL correspond à 1 cm3
Pression d'un gaz

La pression correspond à une grandeur physique qui permet de traduire les échange de quantité de mouvement au sein d'un système thermodynamique, notamment au sein d'un solide ou encore d'un fluide. On peut alors définir la pression comme correspondant à l'intensité de force que va exercer une fluide par unité de surface.
La pression est une grandeur scalaire, voire tensorielle, intensive.
Il faut être prudent lorsque l'on parle de la pression. En effet, nombreux sont ceux qui parlent de pression exercée par un fluide sur une paroi pour parler de la force pressante que le fluide va exercer par unité d'aire de la paroi. Cependant, la force correspond plutôt à une grandeur vectorielle que l'on défini localement alors que la pression correspond à une grandeur scalaire qui est définie en tout point du fluide concerné.
Les unités de pression
L'unité de pression est le Pascal noté (Pa), même si l'on parle parfois du Bar qui, lui, n'est pas une unité du Système International.
L'analyse dimensionnelle de la pression permet de montrer que celle-ci est homogène à une force surfacique (1 Pa = 1 N/m²) comme à une énergie volumique (1 Pa = 1 J/m3).
Quelques formules
La pression p, le volume V, la quantité de matière n, et la température T d'un gaz sont liés par :
[ P times V = n times R times T ]
Avec R = 8,31 USI
Le volume molaire d'un gaz Vm est le volume occupé par 1 mole de ce gaz dans des conditions de température et de pression donnés. On peut déterminer ainsi le volume molaire par la formule suivante : [ V _ { m } = \frac { R times T } { P }]
En sachant que Vm s'exprime en L.mol-1
Pour ce qui est des gaz, le volume V et la quantité de matière n sont liés par : 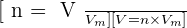
La quantité de mouvement
En physique, on appelle la quantité de mouvement tout produit de la masse par le vecteur vitesse d'un corps matériel que l'on suppose ponctuel. Ainsi, la quantité de mouvement correspond à une grandeur vectorielle que l'on définit par 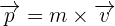 qui dépendra du référentiel d'étude.
qui dépendra du référentiel d'étude.
De plus, en utilisant l'additivité, on est capable de définir la quantité de mouvement d'un corps non ponctuel ou système matériel. De ce fait, il devient possible de démontrer que la quantité de matière est égale à la quantité de mouvement du centre d'inertie de l'objet étudié affecté de la masse totale du système. On a donc 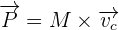 où C correspond au centre d'inertie. On utilise le kg.m.s-1 comme unité.
où C correspond au centre d'inertie. On utilise le kg.m.s-1 comme unité.
De façon logique et naturelle, la notion de quantité de mouvement s'introduit en dynamique. En effet, la relation fondamentale de la dynamique exprime le fait que l'action d'une force extérieure sur un système conduit à une variation de sa quantité de mouvement par l'expression suivante : 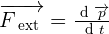
On peut également dire de la notion de quantité de mouvement qu'elle fait partie, de la même façon que l'énergie, des grandeurs qui se conservent dans un système isolé et donc un système qui n'est soumis à aucune action extérieure ou alors ces mêmes actions extérieures sont négligeables ou se compensent. On utilise d'ailleurs fréquemment cette propriété en théorie des collisions.
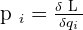 .
.
Dans le cas d'un champ électromagnétique, on appelle la quantité de mouvement impulsion. Elle fait alors référence à la densité volumique d'impulsion du champ donné par la formule :
Quantité de matière et concentration molaire : la dilution
La dilution correspond à un procédé qui consiste en l'obtention d'une solution finale qui présentera une concentration inférieur à la concentration de la solution de départ. Il est alors possible de procéder à cela grâce à un ajout de solvant ou encore en prélevant une partie de la solution puis de compléter jusqu'à atteindre le volume souhaité avec du solvant. Il est alors possible de caractériser une dilution par son taux de dilution. Mais pour cela, il est nécessaire de présupposer que le corps dilué est soluble dans le solvant qui est utilisé.
Dilution par ajout de solvant
On note la concentration d'une solution C et il est possible de la calculer avec la formule suivante : 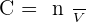
Avec :
- C la concentration molaire. Cette unité s'exprime en mol.L-1 ;
- n la quantité de matière du soluté en solution. Cette unité s'exprime en mol ;
- Et V le volume de solvant. Cette unité s'exprime en L.
Ainsi, si on procède à une dilution par ajout de solvant, la solution initiale et la solution finale contiennent autant de quantité de soluté. Cela signifie alors que ninitiale = nfinale .
On a alors les relations suivantes qui se dégagent :
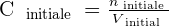

On peut déduire de ces relations le rapport suivant :
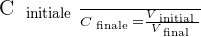
Taux de dilution
Il est possible d'exprimer le taux de dilution avec la relation suivante :
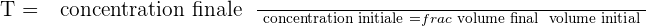
Il est important de savoir que le taux de dilution, noté T, est une grandeur sans unité et qui présente obligatoirement une valeur positive et inférieure à 1.
Quant au taux de dilutions successives, il correspond au produit des taux de dilution de chaque dilution.
Exemple
Si on procède à une dilution à 3 % puis à 5 %, on a T qui est égal à :
























Si vous désirez une aide personnalisée, contactez dès maintenant l’un de nos professeurs !
thermodynamique =
Merci pour ces précieux conseils
On me Donne une masse de 10.5 g, une pression de 85kpa et une volume de 30 l on me demande de calculer la temperature…
Je ne peux rien faire. A l’aide