Chapitres

Définitions

- On dit que deux objets A et B sont en interaction, si l'objet A exerce une action qui se manifeste par ses effets sur l'objet B, et si réciproquement, l'objet B agit sur l'objet A.
- On considère qu'une force correspond à l’action exercée par chacun des corps sur l’autre.
- Puisque toute interaction est réciproque, on choisit d’étudier un participant, le système, et les forces qui s’exercent sur lui. Un système correspond à l’ensembles des objet dont on étudie le mouvement. Ainsi on sépare l’Univers en deux : le système et l’extérieur. Pour résumer, tout ce qui n’est pas le système est appelé extérieur et le système subit des forces exercées par ce qui est intérieur au système, appelées forces extérieures
- Qu’est ce qu’un système déformable ?
- Un système déformable correspond système dont la distance entre deux de ces points quelconques peur varier.
- Qu’est ce qu’un système indéformable ?
- Un système indéformable correspond à un système dont la distance entre deux de ces points quelconque est toujours constante. Un tel système est alors appelé un solide.
- On considère qu'une force localisée correspond à une force qui ne s’applique qu'en un point d’un objet ou sur un objet ponctuel. Par exemple un fil tire un objet avec une force T localisée au point d’accrochage.
- On considère qu'une force répartie correspond à une force qui s’applique sur un ensemble de points répartis sur une surface ou dans un volume de l’objet. Par exemple le poids P est réparti dans tout le volume d’un objet.
- On considère qu'une force à distance correspond à une force qui s’exerce entre 2 objets pouvant être séparés par de l’air, de l’eau, du vide…
Il y a 3 sortes de forces à distance :- les forces de gravitation : Elles s’exercent entre les astres ; entre la terre et les objets terrestres. Le poids d’un corps est essentiellement une force de gravitation. Ce sont des forces attractives.
- les forces électriques : Elles s’exercent entre deux objets portant des charges électriques. Elles peuvent être aussi bien attractives que répulsives.
- les forces magnétiques : Elles s’exercent entre des aimants ou entre des aimants et certains matériaux (en particulier le fer).Elles aussi peuvent être attractives ou répulsives.
- Pour considérer une force comme étant une force de contact, il faut obligatoirement qu’il y ait contact entre les deux objets pour que naisse cette fameuse force de contact. Par exemple la force de traction d’un fil, mesurée par la tension du fil, s’applique au point de contact objet-fil.
- Un effet dynamique correspond à une force qui peut modifier le mouvement d’un système, c’est à dire modifier son vecteur vitesse.
- Les effets statiques existant sont :
- L'équilibre : on considère qu'un système est en équilibre si tous ses points sont au repos dans le référentiel d’étude.
- Les effets d’une force : on considère q'une force peut contribuer à l’équilibre d’un système et déformer un système en équilibre ou non.
- Qu’est ce qu’un solide ponctuel ?
- Un solide ponctuel correspond à un solide dont les dimensions sont très inférieures aux autres dimensions du problème et qui peut donc être considéré comme un point.
En physique chimie cours, quand on parle d'action à distance, on parle également de champs. C'est pour cela qu'il peut être très intéressant et utile de rappeler les différents types de champs existant ainsi que leurs caractéristiques.
Il peut alors être intéressant de rappeler la définition des différents champs existant :
Le champ électrique
En physique, on appelle champ électrique tout champ vectoriel créé par des particules électriquement chargées. Plus exactement, lorsque nous sommes en présence d'une particule chargée, les propriétés locale de l'espace défini sont alors modifié ce qui permet de définir la notion de champ. En effet, si une autre charge se trouve être dans le dit champ, elle subira ce qu'on appelle l'action de la force électrique qui est exercée par la particule malgré la distance. On dit alors du champ électrique qu'il est le médiateur de la dite action à distance.
Si on se veut plus précis, on peut définir dans un référentiel galiléen défini, une charge q définie de vecteur vitesse v qui subit de la part des autres charges présentes, qu'elles soient fixes ou mobiles, une force qu'on définira de force de Lorentz. Cette force se décompose ainsi :
[ overrightarrow { f } = q left ( overrightarrow { E } + overrightarrow { v } wedge overrightarrow { B } right) ]
avec :
- [ overrightarrow { E } ] le champ électrique. Celui-ci décrit dans ce cas la partie de la force de Lorentz qui est indépendante de la vitesse de la charge
- [ overrightarrow { B } ] le champ magnétique. Celui-ci décrit ainsi la partie de la force exercée sur la charge qui dépend du déplacement de cette même charge dans le référentiel choisi.
De plus, il est important de noter que les deux champs, électrique et magnétique, dépendent du référentiel d'étude.
Avec cette formule, on peut alors définir le champ électrique comme étant le champ traduisant l'action à distance subie par une charge électrique fixe dans un référentiel défini de la part de toutes les autres charges, qu'elles soient mobiles ou fixes.
Mais on peut également définir le champ électrique comme étant toute région de l'espace dans laquelle une charge est soumise à une force dite de Coulomb.
On commence à parler de champ électrostatique lorsque, dans un référentiel d'étude, les charges sont fixes. Notons d'ailleurs que le champ électrostatique ne correspond pas au champ électrique comme décrit plus haut dans cet article puisqu'en effet, lorsque les charges sont en mouvement dans un référentiel, il faut ajouter à ce référentiel un champ électrique qui est induit par les déplacement des charges afin d'obtenir un champ électrique complet.
Mais, le champ électrique reste dans la réalité un caractère relatif puisqu'il ne peut exister indépendamment du champ magnétique. En effet, si on observe la description correcte d'un champ électromagnétique, celui-ci fait intervenir un tenseur quadridimensionnel de champ électromagnétique dont les composantes temporelles correspondent alors à celle d'un champ électrique. Seul ce tenseur possède un sens physique. Alors, dans le cas d'un changement de référentiel, il est tout à fait possible de transformer un champ magnétique en champ électrique et inversement.
Le champ électromagnétique

En physique, on appelle champ électromagnétique la représentation dans l'espace d'une force électromagnétique exercée par des particules chargées. Ce champ représente alors l'ensemble des composantes de la force électromagnétique qui s'appliquent à une particule chargée qui se déplace alors dans un référentiel galiléen.
On peut alors définir la force subit par une particule de charge q et de vecteur vitesse par l'expression suivante :
[ overrightarrow { f } = q left ( overrightarrow { E } + overrightarrow { v } wedge overrightarrow { B } right) ]
avec :
[ overrightarrow { E } ] le champ électrique. Celui-ci décrit dans ce cas la partie de la force de Lorentz qui est indépendante de la vitesse de la charge
[ overrightarrow { B } ] le champ magnétique. Celui-ci décrit ainsi la partie de la force exercée sur la charge qui dépend du déplacement de cette même charge dans le référentiel choisi.
En effet la séparation de la partie magnétique et de la partie électrique de dépend que du point de vue pris selon le référentiel d'étude.
De plus, il peut être intéressant de savoir que les équations de Maxwell régissent les deux composantes couplées, c'est à dire électrique et magnétique, de sorte que toute variation d'une composante induira la variation de l'autre composante.
D'ailleurs, le comportement des champs électromagnétiques se trouve décrit de façon classique par les équations de Maxwell et de manière plus générale par l'électrodynamique quantique.
La façon la plus utilisée afin de définir le champ électromagnétique est celle du tenseur électromagnétique de la relativité restreinte.
Le champ électrostatique
On parle de champ électrostatique lors que les charges qui constitue le champ sont au repos dans le référentiel d'étude. Ce champ est donc déduit de l'expression de la loi de Coulomb, aussi appelée interaction électrostatique.
Le champ gravitationnel
En physique classique, on appelle champ gravitationnel, ou encore champ de gravitation, un champ qui est réparti dans l'espace et dû à la présence d'une masse qui est alors susceptible d'exercer une influence gravitationnelle sur tout les autres corps pouvant être présent à proximité immédiate ou non.
On peut démontrer que le champ gravitationnel créé en un point quelconque par un corps ponctuel dérive d'un potentiel scalaire dit newtonien.
En physique classique, le champ gravitationnel ou champ de gravitation est un champ réparti dans l'espace et dû à la présence d'une masse susceptible d'exercer une influence gravitationnelle sur tout autre corps présent à proximité (immédiate ou pas). L'introduction de cette grandeur permet de s'affranchir du problème de la médiation de l'action à distance apparaissant dans l'expression de la force de gravitation universelle.
On peut interpréter le champ gravitationnel comme étant la modification de la métrique de l'espace-temps. L'approximation newtonienne est alors valable uniquement dans le cas où les corps présentent une vitesse faible par rapport à celle de la lumière dans le vide et si le potentiel gravitationnel qu'ils créent est tel que le quotient du potentiel gravitationnel sur le carré de la vitesse de la lumière dans le vide est négligeable.
On peut approcher le champ électrique et le champ gravitationnel. En effet, l'expression du champ et du potentiel ne sont différents que d'une constante. De plus, les principaux théorèmes de calculs, celui de la superposition ou de Gauss par exemple, peuvent s'appliquer dans les deux cas. Ce qui les différencie alors est le caractère attractif, donc entre deux charges de signe opposé, ou répulsif, donc entre deux charges de même signe, du champ électrique tandis que le champ gravitationnel ne peut être qu'attractif.
Explications

Pour une force localisée
Nous considérons un fil AM qui tire sur un solide. Cette force sera modélisé par un vecteur F. Celui-ci aura :
- une direction : la direction du fil AM
- un sens : de A vers M
- une intensité ou un module F par exemple mesuré avec un dynamomètre
- un point d’application : la point A
Pour une force répartie
Si nous considérons l’action exercée par une main qui posée à plat appuie sur un mur, la force exercée par la main sur le mur est répartie sur toute la surface de contact entre la main et le mur. On peut encore définir une direction, un sens, un module ; mais on ne peut plus parler de point d’application. On dessinera le vecteur F à partir d’un point quelconque de la surface de contact.
Si un système matériel A exerce la force 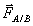
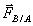
Les deux forces réciproques qui naissent de l’interaction entre A et B sont opposées. On a donc [ overrightarrow { F } _ { A / B } = - overrightarrow { F } _ { B / A } ]
Le principe d’interaction
Un système ne participe pratiquement jamais à une seule interaction. Son état de mouvement ou de repos est conditionné par l’ensemble des forces extérieures qui s’exercent sur lui.
Il est donc nécessaire de dresser le bilan de celles-ci, en ne tenant compte que des forces dont l’effet est manifeste dans les conditions de l’étude.
En pratique pour dresser un bilan des forces il faut :
- Préciser le système
- Recenser tous les objets avec lesquels il est en interaction
- Énumérer les forces à distance
- Énumérer les forces de contacts
- S’assurer que chaque forces est une force extérieure au système
- Préciser pour chaque force :
- sa direction
- son sens
- sa valeur
- son point d’application
Approfondissement de la notion d'action de contact

Actions de contact localisées
Les actions de contact localisées correspondent à des actions qui s'exercent sur un point précis ou encore sur une petite surface du receveur comme dans le cas du perchiste et de sa perche ou encore dans le cas de la caravane tirée par une voiture.
Actions de contact réparties
Les actions de contact réparties correspondent à des actions qui s'exercent sur une grande surface du receveur comme dans le cas du le vent dans la voile ou dans le cas de l'eau sur la planche de surf.
Les actions à distance
On peut parler d'action à distance lorsque l'on se trouve dans un cas où il n'y a pas de contact entre l'acteur et le receveur et dans le cas ou ces actions se sont des actions réparties dans toute la matière de l'objet. Il existe alors différents types actions à distance :
- Les actions électriques comme dans le cas où fin filet d'eau attiré par une règle en plastique frottée avec de la laine, on parle alors d'électricité statiques causée par un champ ;
- Les actions magnétiques comme dans le cas où aimant attire les objets en fer et en nickel ;
- Ou encore les actions gravitationnelles qui s'exercent sur tous les corps dont la masse n'est pas nulle, on peut présenter l'exemple de l'attraction terrestre.
Etudier le mouvement provoqué par les contacts et les interactions
Pour étudier le mouvement d’un système on a toujours besoin de se fixer un référentiel : c’est un objet par
rapport auquel on étudiera le mouvement de notre système.
Définition : La trajectoire d’un point matériel est l’ensemble des positions successives occupées par ce point au cours du temps. Elle dépend du référentiel choisi.
En simplifiant, on peut définir le référentiel comme quelque chose correspondant au milieu au sein duquel on étudie le mouvement.
En effet, si on choisi de prendre l'exemple du voyageur assit dans un train en marche alors le référentiel vas changer selon l'observateur :
- par rapport à un observateur sur le quai, le voyageur est en mouvement
- par rapport à un observateur dans le train, le voyageur est immobile.
Ainsi, il est possible de conclure que, pour décrire le mouvement d’un mobile, il faut choisir un repère d’espace ou référentiel.
La trajectoire correspond à l’ensemble de toutes les positions successives qu’occupe un point du mobile au cours du temps. La trajectoire peut-être curviligne, c'est à dire en vague, circulaire, donc en forme de rond, ou rectiligne.
- mouvement rectiligne : la trajectoire est une droite
- mouvement circulaire : la trajectoire est un arc de cercle
- mouvement curviligne : la trajectoire est une courbe quelconque, plane ou non.
Deux types de mouvement sont très importants dans l’étude des systèmes :
- la translation : Dans un mouvement de translation, chaque segment de droite, appartenant au mobile, reste parallèle à lui-même, au cours du déplacement et tous les points du mobile ont des trajectoires identiques de même longueur.
- la rotation : Dans un mouvement de rotation, tous les points du mobile décrivent des cercles ou des arcs de cercles centrés sur une droite fixe que l'on appelle axe de rotation. On peut notamment illustrer ce mouvement avec l'exemple des aiguilles d’une horloge.
- Si la trajectoire est une droite, la translation est rectiligne, comme dans le cas d'un ascenseur.
- Si la trajectoire est une courbe, la translation est curviligne, comme dans le cas d'un téléphérique.
- Si la trajectoire est un cercle ou un arc de cercle, la translation est circulaire, comme dans le cas d'une grande roue.
Définition : Une translation correspond à une droite passant par 2 points quelconques du solide qui reste parallèle au cours du mouvement
Définition : Une rotation correspond à un mouvement où tous les points décrivent des cercles dont les centres sont alignés et tous les plans sont parallèles.
Résumer avec l'IA :























Si vous désirez une aide personnalisée, contactez dès maintenant l’un de nos professeurs !
Cour assez détaillé et facile à comprendre.merci 😊😊
oui