Chapitres
?️♂️ Le centre d'inertie, également appelé "centre de masse", est un point hypothétique dans un objet où la masse totale peut être considérée comme concentrée pour simplifier l'analyse des mouvements. Il est défini par les positions relatives des différentes parties de l'objet, pondérées par leur masse respective.
? Ce point est crucial en physique, car un objet en mouvement se comporte comme s'il était affecté uniquement par les forces extérieures par rapport à son centre d'inertie. La stabilité, l'équilibre et la prévisibilité des mouvements dépendent souvent de la localisation de ce point clé dans un système physique.
Voici tout ce qu'il faut savoir sur le centre d'inertie et les éléments en mouvement !

Basiques de l'inertie : loi de Newton et référentiel galiléen ?️

En physique, on appelle inertie d'un corps, dans un référentiel galiléen, une tendance de ce corps à conserver sa vitesse. En effet, lorsqu'il y a absence d'influences extérieures, on parle aussi de forces extérieures, alors tout corps que l'on considère comme ponctuel va perdurer dans un mouvement rectiligne uniforme.
Notons que l'on appelle aussi l'inertie, "principe d'inertie" ou encore "loi d'inertie".
Puis, lorsque Newton est arrivé, on l'appelle également première loi de Newton.
La première loi de Newton s'énonce ainsi :
Un système isolé ou pseudo-isolé initialement au repos ou en mouvement rectiligne uniforme demeure dans son état.
✅ On appelle référentiel galiléen tout référentiel au sein duquel le principe d'inertie est vérifié. Même s'il n'existe aucun référentiel galiléen au sens strict. Il est cependant possible de considérer certains référentiels usuels comme galiléens si certaines conditions sont vérifiées :
? Le référentiel terrestre
? Le référentiel géocentrique
☀️ Le référentiel héliocentrique
- Le référentiel terrestre peut être considéré galiléen si on considère un mouvement dont la durée ne dépasse pas quelques minutes dans le but de s'affranchir du mouvement de rotation propre de la Terre.
- Le référentiel géocentrique peut également être considéré comme étant galiléen si on considère un mouvement dont la durée ne dépasse quelques heures dans le but de s'affranchir du mouvement de rotation de la Terre autour du Soleil.
- Le référentiel héliocentrique peut aussi être considéré comme étant galiléen car l'impact du mouvement de rotation du Soleil au sein de la galaxie est négligeable.
Le mouvement d'un solide ?
Lorsqu’un solide est soumis à des actions extérieures qui se compensent, on dit qu’il est pseudo-isolé. Un solide qui ne subirait aucune action extérieure serait dit "isolé", ce serait approximativement le cas d’un solide perdu, très très loin de toute étoile ou planète, dans l’espace interstellaire.
Le centre d’inertie d'un objet, et ce quelle que soit l’histoire antérieure du système, s’il est pseudo isolé, correspond à un et un seul des points de sa trajectoire qui est toujours en mouvement rectiligne et uniforme. C’est par exemple au centre d’inertie d’un solide que s’exerce le poids du système.
- On dit que deux objets A et B sont en interaction, si l'objet A exerce une action qui se manifeste par ses effets sur l'objet B, et si réciproquement, l'objet B agit sur l'objet A
- On considère qu'une force correspond à l’action exercée par chacun des corps sur l’autre
- Puisque toute interaction est réciproque, on choisit d’étudier un participant, le système, et les forces qui s’exercent sur lui. Un système correspond à l’ensembles des objet dont on étudie le mouvement.
- Ainsi on sépare l’Univers en deux : le système et l’extérieur. Pour résumer, tout ce qui n’est pas le système est appelé extérieur et le système subit des forces exercées par ce qui est intérieur au système, appelées forces extérieures
⚠️ À retenir :
Qu’est ce qu’un système déformable ? Un système déformable correspond à un système dont la distance entre deux de ces points quelconques peur varier
Qu’est ce qu’un système indéformable ? Un système indéformable correspond à un système dont la distance entre deux de ces points quelconque est toujours constante. Un tel système est alors appelé un solide
? On considère alors plusieurs types de forces :
- On considère qu'une force localisée correspond à une force qui ne s’applique qu'en un point d’un objet ou sur un objet ponctuel. Par exemple un fil tire un objet avec une force T localisée au point d’accrochage.
- On considère qu'une force répartie correspond à une force qui s’applique sur un ensemble de points répartis sur une surface ou dans un volume de l’objet. Par exemple le poids P est réparti dans tout le volume d’un objet.
- On considère qu'une force à distance correspond à une force qui s’exerce entre 2 objets pouvant être séparés par de l’air, de l’eau, du vide… Il y a 3 sortes de forces à distance :
- Les forces de gravitation : Elles s’exercent entre les astres ; entre la terre et les objets terrestres. Le poids d’un corps est essentiellement une force de gravitation. Ce sont des forces attractives.
- Les forces électriques : Elles s’exercent entre deux objets portant des charges électriques. Elles peuvent être aussi bien attractives que répulsives.
- Les forces magnétiques : Elles s’exercent entre des aimants ou entre des aimants et certains matériaux (en particulier le fer).Elles aussi peuvent être attractives ou répulsives.
? Pour étudier le mouvement d’un système on a toujours besoin de se fixer un référentiel : c’est un objet par rapport auquel on étudiera le mouvement de notre système.
Définition : La trajectoire d’un point matériel est l’ensemble des positions successives occupées par ce point au cours du temps. Elle dépend du référentiel choisi.
En simplifiant, on peut définir le référentiel comme quelque chose correspondant au milieu au sein duquel on étudie le mouvement. En effet, si on choisi de prendre l'exemple du voyageur assit dans un train en marche alors le référentiel vas changer selon l'observateur :
- Par rapport à un observateur sur le quai, le voyageur est en mouvement
- Par rapport à un observateur dans le train, le voyageur est immobile.
✍️ Ainsi, il est possible de conclure que, pour décrire le mouvement d’un mobile, il faut choisir un repère d’espace ou référentiel. La trajectoire correspond à l’ensemble de toutes les positions successives qu’occupe un point du mobile au cours du temps. La trajectoire peut-être curviligne, c'est à dire en vague, circulaire, donc en forme de rond, ou rectiligne :
- Mouvement rectiligne : la trajectoire est une droite
- Mouvement circulaire : la trajectoire est un arc de cercle
- Mouvement curviligne : la trajectoire est une courbe quelconque, plane ou non.
Deux types de mouvement sont très importants dans l’étude des systèmes :
- La translation : Dans un mouvement de translation, chaque segment de droite, appartenant au mobile, reste parallèle à lui-même, au cours du déplacement et tous les points du mobile ont des trajectoires identiques de même longueur.
- La rotation : Dans un mouvement de rotation, tous les points du mobile décrivent des cercles ou des arcs de cercles centrés sur une droite fixe que l'on appelle axe de rotation. On peut notamment illustrer ce mouvement avec l'exemple des aiguilles d’une horloge.
- Si la trajectoire est une droite, la translation est rectiligne, comme dans le cas d'un ascenseur.
- Si la trajectoire est une courbe, la translation est curviligne, comme dans le cas d'un téléphérique.
- Si la trajectoire est un cercle ou un arc de cercle, la translation est circulaire, comme dans le cas d'une grande roue.
Définition : Une translation correspond à une droite passant par 2 points quelconques du solide qui reste parallèle au cours du mouvement
Définition : Une rotation correspond à un mouvement où tous les points décrivent des cercles dont les centres sont alignés et tous les plans sont parallèles.
Le mouvement et les forces extérieures
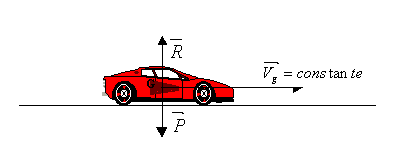
? Un système est pseudo-isolé si la somme vectorielle des forces extérieures qui s’exercent sur lui est égale au vecteur nul.

Notons que  se lit "somme des forces extérieures" et symbolise la somme vectorielle de toutes les forces extérieures s’exerçant sur le système
se lit "somme des forces extérieures" et symbolise la somme vectorielle de toutes les forces extérieures s’exerçant sur le système
?️ En conséquence, le vecteur vitesse 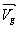
Dans ce cas, la somme vectorielle des forces extérieures s’exerçant sur le système n’est pas égale au vecteur nulle :
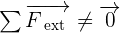
? En conséquence le vecteur vitesse 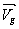
Le cas d'une force localisée
? Nous considérons un fil AM qui tire sur un solide. Cette force sera modélisé par un vecteur F. Celui-ci aura :
- une direction : la direction du fil AM
- un sens : de A vers M
- une intensité ou un module F par exemple mesuré avec un dynamomètre
- un point d’application : la point A
Le cas d'une force répartie
✋ Si nous considérons l’action exercée par une main qui posée à plat appuie sur un mur, la force exercée par la main sur le mur est répartie sur toute la surface de contact entre la main et le mur. On peut encore définir une direction, un sens, un module, mais on ne peut plus parler de point d’application.
On dessinera le vecteur F à partir d’un point quelconque de la surface de contact :
- Si un système matériel A exerce la force
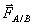
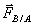
- Les deux forces réciproques qui naissent de l’interaction entre A et B sont opposées
- On a donc

Interaction entre l'objet en mouvement et les forces extérieures
Un système ne participe pratiquement jamais à une seule interaction. Son état de mouvement ou de repos est conditionné par l’ensemble des forces extérieures qui s’exercent sur lui. Il est donc nécessaire de dresser le bilan de celles-ci, en ne tenant compte que des forces dont l’effet est manifeste dans les conditions de l’étude.
? En pratique, pour dresser un bilan des forces il faut :
- Préciser le système
- Recenser tous les objets avec lesquels il est en interaction
- Énumérer les forces à distance
- Énumérer les forces de contacts
- S’assurer que chaque forces est une force extérieure au système
- Préciser pour chaque force :
- sa direction
- son sens
- sa valeur
- son point d’application
Les actions de contact ?
Actions de contact localisées
Les actions de contact localisées correspondent à des actions qui s'exercent sur un point précis ou encore sur une petite surface du receveur comme dans le cas du perchiste et de sa perche ou encore dans le cas de la caravane tirée par une voiture.
Actions de contact réparties
?♂️ Les actions de contact réparties correspondent à des actions qui s'exercent sur une grande surface du receveur comme dans le cas du le vent dans la voile ou dans le cas de l'eau sur la planche de surf.
Les actions à distance
? On peut parler d'action à distance lorsque l'on se trouve dans un cas où il n'y a pas de contact entre l'acteur et le receveur et dans le cas ou ces actions se sont des actions réparties dans toute la matière de l'objet. Il existe alors différents types actions à distance :
- Les actions électriques comme dans le cas où fin filet d'eau attiré par une règle en plastique frottée avec de la laine, on parle alors d'électricité statiques causée par un champ
- Les actions magnétiques comme dans le cas où aimant attire les objets en fer et en nickel
- Ou encore les actions gravitationnelles qui s'exercent sur tous les corps dont la masse n'est pas nulle, on peut présenter l'exemple de l'attraction terrestre
La chute libre et ses principes ?
On appelle chute libre le mouvement que prend un objet sous la seule action de son poids. Un tel mouvement ne peut avoir lieu que dans le vide. On peut admettre que dans l’air, la chute est "libre" si l’on peut négliger :
- Les frottements
- La poussée d’Archimède (il faut que la masse volumique de l’objet soit grande devant celle de l’air)
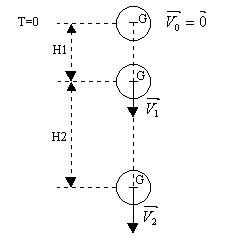
On a donc une variation du vecteur vitesse du centre d’inertie G de la bille : la valeur de la vitesse varie, la direction reste constante. On peut monter que pour une hauteur de chute h ( en partant sans vitesse initiale), on a les deux relations suivantes ou v représente la vitesse :
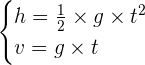
La poussée d’Archimède
?La poussée d'Archimède est un phénomène physique qui décrit le comportement de tout corps plongé dans un fluide qu'il soit liquide ou gazeux soumis à un champ de gravité. Elle est nommée ainsi en l'honneur d'Archimède de Syracuse, un très grand scientifique grec de 200 avant J.-C.
? Elle est causée par l'augmentation de la pression du fluide avec la profondeur. Comme la pression exercée sur la partie basse du corps est supérieure à celle exercée sur la partie haute, le corps est poussé verticalement vers le haut.
Voici la formulation d'origine de cette loi physique :
Tout corps plongé dans un fluide au repos, entièrement mouillé par celui-ci ou traversant sa surface libre, subit une force verticale, dirigée de bas en haut et opposée au poids du volume de fluide déplacé : cette force est appelée poussée d'Archimède.
?? Pour que le théorème s'applique il faut que le fluide immergeant et le corps immergé soient au repos. Il faut également qu'il soit possible de remplacer le corps immergé par du fluide immergeant sans rompre l'équilibre. Voici l'équation qui en résulte :
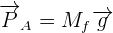
Avec :
- Mf< la masse du fluide contenu dans un volume V et déplacé ;
- g la valeur du champ de pesanteur, de 9,81 N/kg à la surface de la Terre.
Résumer avec l'IA :























Si vous désirez une aide personnalisée, contactez dès maintenant l’un de nos professeurs !
JE VEUT DE L’AIDE À MA MÉMOIR
Bonjour, envisagez de vous appuyer sur nos professeurs chez Superprof pour un accompagnement qui répond spécifiquement à vos besoins. Passez une agréable journée ! :)
J’aimerais que vou m’aidez en physique et en chimie
Bonjour Jean, merci pour votre intérêt. Il nous fera plaisir de vous aider ! Avez-vous essayé de contacter l’un de nos professeurs pour recevoir une aide personnalisée en physique chimie ? Excellente journée ! 🙂
merci beaucoup pour votre article