Chapitres

Le champ magnétique
Champ électrique
En cours physique chimie, on appelle champ électrique tout champ vectoriel créé par des particules électriquement chargées. Plus exactement, lorsque nous sommes en présence d'une particule chargée, les propriétés locale de l'espace défini sont alors modifié ce qui permet de définir la notion de champ. En effet, si une autre charge se trouve être dans le dit champ, elle subira ce qu'on appelle l'action de la force électrique qui est exercée par la particule malgré la distance. On dit alors du champ électrique qu'il est le médiateur de la dite action à distance.

Si on se veut plus précis, on peut définir dans un référentiel galiléen défini, une charge q définie de vecteur vitesse v qui subit de la part des autres charges présentes, qu'elles soient fixes ou mobiles, une force qu'on définira de force de Lorentz. Cette force se décompose ainsi :
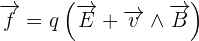
avec :
 le champ électrique. Celui-ci décrit dans ce cas la partie de la force de Lorentz qui est indépendante de la vitesse de la charge
le champ électrique. Celui-ci décrit dans ce cas la partie de la force de Lorentz qui est indépendante de la vitesse de la charge le champ magnétique. Celui-ci décrit ainsi la partie de la force exercée sur la charge qui dépend du déplacement de cette même charge dans le référentiel choisi.
le champ magnétique. Celui-ci décrit ainsi la partie de la force exercée sur la charge qui dépend du déplacement de cette même charge dans le référentiel choisi.
De plus, il est important de noter que les deux champs, électrique et magnétique, dépendent du référentiel d'étude.
Avec cette formule, on peut alors définir le champ électrique comme étant le champ traduisant l'action à distance subie par une charge électrique fixe dans un référentiel défini de la part de toutes les autres charges, qu'elles soient mobiles ou fixes.
Mais on peut également définir le champ électrique comme étant toute région de l'espace dans laquelle une charge est soumise à une force dite de Coulomb.
On commence à parler de champ électrostatique lorsque, dans un référentiel d'étude, les charges sont fixes. Notons d'ailleurs que le champ électrostatique ne correspond pas au champ électrique comme décrit plus haut dans cet article puisqu'en effet, lorsque les charges sont en mouvement dans un référentiel, il faut ajouter à ce référentiel un champ électrique qui est induit par les déplacement des charges afin d'obtenir un champ électrique complet.
Mais, le champ électrique reste dans la réalité un caractère relatif puisqu'il ne peut exister indépendamment du champ magnétique. En effet, si on observe la description correcte d'un champ électromagnétique, celui-ci fait intervenir un tenseur quadridimensionnel de champ électromagnétique dont les composantes temporelles correspondent alors à celle d'un champ électrique. Seul ce tenseur possède un sens physique. Alors, dans le cas d'un changement de référentiel, il est tout à fait possible de transformer un champ magnétique en champ électrique et inversement.
Où trouver un cours physique chimie 6ème ?
Le champ électromagnétique
En physique, on appelle champ électromagnétique la représentation dans l'espace d'une force électromagnétique exercée par des particules chargées. Ce champ représente alors l'ensemble des composantes de la force électromagnétique qui s'appliquent à une particule chargée qui se déplace alors dans un référentiel galiléen.
On peut alors définir la force subit par une particule de charge q et de vecteur vitesse par l'expression suivante :
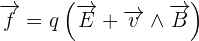
avec :
 le champ électrique. Celui-ci décrit dans ce cas la partie de la force de Lorentz qui est indépendante de la vitesse de la charge
le champ électrique. Celui-ci décrit dans ce cas la partie de la force de Lorentz qui est indépendante de la vitesse de la charge
 le champ magnétique. Celui-ci décrit ainsi la partie de la force exercée sur la charge qui dépend du déplacement de cette même charge dans le référentiel choisi.
le champ magnétique. Celui-ci décrit ainsi la partie de la force exercée sur la charge qui dépend du déplacement de cette même charge dans le référentiel choisi.
En effet la séparation de la partie magnétique et de la partie électrique de dépend que du point de vue pris selon le référentiel d'étude.
De plus, il peut être intéressant de savoir que les équations de Maxwell régissent les deux composantes couplées, c'est à dire électrique et magnétique, de sorte que toute variation d'une composante induira la variation de l'autre composante.
D'ailleurs, le comportement des champs électromagnétiques se trouve décrit de façon classique par les équations de Maxwell et de manière plus générale par l'électrodynamique quantique.
La façon la plus utilisée afin de définir le champ électromagnétique est celle du tenseur électromagnétique de la relativité restreinte.
Comportement des aimants
En cours physique chimie lycée, des aimants peuvent s'attirer ou se repousser selon la face que l'on présente l'un à l'autre.
Un aimant possède deux pôles : nord et sud, deux pôles identiques se repoussent et deux pôles opposés s'attirent.
Seuls les matériaux contenant du fer ont des propriétés magnétiques.
Définition d'un champ
Un champ décrit une région de l'espace dans laquelle une source engendre sur un objet physique une action. Chaque point de la région concernée possède une valeur numérique ou vectorielle attribuée à la grandeur physique qui décrit le champ.
Si les points de l'espace portent une valeur numérique, le champ est dit scalaire (temps), s'ils portent un vecteur, le champ est dit vectoriel.
Champ B
En un point de l'espace M autour d'une source magnétique, on peut définir le champ magnétique de B en M. Les caractéristiques sont les suivantes :
- Sa direction est indiquée par l'aiguille d'une boussole aimantée
- Son sens est toujours du nord vers le sud de la source
- L'intensité (unité Tesla), elle diminue quand on s'éloigne de la source
Lignes de champ
Les lignes tangentes au vecteur B en tout point de l'espace se nomment lignes de champ.
Elles sont orientées comme le champ B du nord vers le sud de la source et l'ensemble de ces lignes se nomme le spectre magnétique de la source.
Superposition de champs
Principe de superporsition
Il est possible d'appliquer le principe de superposition à un système de type entrée-sortie si :
- La somme de deux entrées quelconque correspond à la somme des deux sorties correspondantes ;
- Un multiple d'une entrée quelconque correspond le même multiple de la sortie correspondante.
Dans ce cas, c'est-à-dire celui d'un système physique, on peut appeler l'entrée excitation et la sortie réponse.
On obtient alors, en notant les excitations ƒ et les réponses x (donc les mouvements généré par les forces mécaniques ƒ) :
- Lorsque l'on sollicite le système par une entrée, donc une excitation notée ƒ1, une réponse, donc un déplacement, qui sera noté x1 ;
- Lorsque l'on sollicite le système par une entrée, donc une excitation notée ƒ2, une réponse, donc un déplacement, qui sera noté x2 .
Champ uniforme
Un champ est uniforme lorsque ses lignes de champ sont parallèles et il a la même valeur en tout point. C'est le cas par exemple dans un aimant en U
Superposition de champ
La superposition de deux champs magnétiques crée un champ unique représentée par un vecteur égal à la somme vectorielle des deux champs superposés.
Le théorème de Gauss
Le théorème de Gauss permet, en électromagnétisme, de calculer le flux d'un champ électrique à travers une surface qui est fermée et ce grâce à la connaissance des charges électriques que cette surface renferme.
Il s'énonce ainsi :
Le flux du champ électrique à travers une surface S fermée est égal à la somme des charges électriques contenues dans le volume V délimité par cette surface, divisée par la permittivité du vide.
Loi de Coulomb
Coulomb, un physicien français, a établi en 1758 que le champ doit varier comme le carré inverse de la distance entre les charges à une précision de 0,02 sur l'exposant avec l'aide d'un dispositif appelé balance de Coulomb. Cette balance est constituée d'un fil de torsion en argent sur lequel est fixé des matériaux chargés. Ainsi, la loi d'attraction entre deux charges ponctuelles notées q1 et q2 , fixes dans le référentiel défini et séparées par une distance r, se définit ainsi :
- La force est dirigée selon la droite reliant les deux charges ;
- Elle est attractive si les charges sont de signes opposée et répulsive sinon ;
- Son intensité est proportionnelle aux valeurs de q1 et q2 et varie en raison inverse du carré de la distance r.
Il est alors possible de traduire ces caractéristiques en une formule exprimant la force exercée par q1 sur q2 :

avec :
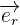 le vecteur unitaire de la droite reliant q1 et q2 qui est dirigée dans le sens 1 vers 2
le vecteur unitaire de la droite reliant q1 et q2 qui est dirigée dans le sens 1 vers 2 la permittivité diélectrique du vide
la permittivité diélectrique du vide
Ce qui peut rendre la compréhension de cette formule compliquée est la notion de force à distance. En effet, comment une charge peut savoir qu'une autre charge ponctuelle se trouve à une certaine distance d'elle et alors exercer sur force sur cette charge en fonction de la distance qui les sépare.
Dans ce cas, tout comme pour un champ gravitationnel, il peut être utile de séparer dans la loi de force ce qui dépend de la charge subissant la force et donc d'obtenir la relation suivante :

avec :
 un champ électrique électrostatique créé à partie de la charge q1 au point où se trouve la seconde charge q2
un champ électrique électrostatique créé à partie de la charge q1 au point où se trouve la seconde charge q2
Ainsi, avec cette relation, il est plus aisé d'interpréter l’existence d'une force à distance. En effet, la charge considérée comme "source", c'est-à-dire q1, crée en tout point de l'espace un champ électrique dont la forme est donnée par la relation exprimée ci-dessus, et une charge quelconque considérée comme "test" subira l'effet de ce champ sous la forme d'une force égale au produit de cette charge par le champ électrostatique. Dans ce cas, ce champ électrostatique apparaîtra comme la force entre deux particules ponctuelles fixes par unité de charge.
Le Tesla et le champ magnétique terrestre

Le Tesla est une unité grande c'est à dire que peu de tesla peut produire beaucoup d'effet. Les aimants usuels sont de quelques mT.
La Terre peut être considérée comme un aimant dont le pôle Nord magnétique est proche du pôle Sud géographique.
Le champ magnétique terrestre a pour valeur BT= 2 10-5 T.
- Champ magnétique crée par un courant
- Champ crée par un courant rectiligne
L'expérience historique de Oessted (1777-1851) a permis de découvrir qu'un fil parcouru par un courant produit un champ magnétique dont les caractéristiques sont les suivantes :
- direction : les lignes de champ sont des cercles concentriques centrés sur l'axe du fil. Le champ est perpendiculaire à un rayon issu du fil est joignant le point M.
- le sens est donné par la règle de la main droite : si le courant sort par le pouce, le champ est dirigé suivant les doigts.
- valeur augmente avec l'intensité du courant mais diminue quand la distance du fil augmente.
Champ crée par un solénoïde
Définition
Un solénoïde est un enroulement cylindrique d'un fil conducteur de N spires circulaires sur une longueur L ayant un diamètre D.
L ≥ 2D → long
L ≤ 2D → court
Champ d'un solénoïde
Un solénoïde a le même champ magnétique qu'un aimant droit à la différence près que l'intérieur du solénoïde est le siège du champ permanent et homogène.
Caractéristiques :
- Le sens est déterminé par la circulation du courant si le courant tourne dans le sens des aiguilles d'une montre dans le solénoïde alors on observe un face sud et inversement.
- La direction de ce champ est tangente en tout point à la ligne de champ.
- La valeur du champ dépend des caractéristiques du solénoïde.
Cette valeur est valable dans stout le voisinage de l'axe du solénoïde (là où le champ est uniforme).
Force de Laplace
Le physicien français Laplace a démontré au 18ème siècle qu'il existait une force mécanique induite par un champ magnétique et exercée par un conducteur parcouru par un courant. Cette force s'appelle Force Laplace.
Les caractéristiques de cette force :
- point d'application : répartit sur tout le conducteur et on choisira un point moyen d'application au centre de symétrie du conducteur.
- la direction de la force ainsi que son sens est donné par la règle du trièdre direct (main droite)
- la valeur de la force est donnée par les caractéristiques de l'intensité I, de la longueur l du conducteur soumise au champ B et de la valeur du champ B lui même.
F = I l B sin(α)
L'angle α est l'angle entre le courant électrique et le champ magnétique (entre I et B)
On détermine cette règle par le trois doigts de la main droite :
- l'intensité sort par le pouce
- le champ B par l'index
- la force par le majeur
Quelques propriétés du champ magnétique
Les propriétés du champ magnétique
Distribution de courant filiforme
- L'intensité électrique est adaptée pour décrire une répartition de courants localisée dans un tube de faible section (cas des fils électriques), tube qui sera "vu" de loin comme un fil dont on néglige l'épaisseur,
- Définition de l'intensité électrique.
Invariances par translation et rotation
- Si une distribution de courants est invariante par translation dans une direction donnée, le champ magnétique créé sera également invariant dans cette direction,
- Si une distribution de courants est invariante par rotation autour d'un axe, la norme du champ magnétique créé sera également invariante par rotation.
Propriétés du champ magnétique en tout point d'un plan de symétrie ou d'un plan d'antisymétrie des courants
Définitions
- Un plan de symétrie d'une distribution de courants est un plan qui laisse invariante cette distribution de courants lorsqu'on effectue la symétrie plane,
- Un plan d'antisymétrie d'une distribution de courants est un plan qui laisse invariante cette distribution de courants mais en inversant les sens des courants lorsqu'on effectue la symétrie plane.
Propriétés
- En un point appartenant à un plan de symétrie d'une distribution de courants, le champ magnétostatique est orthogonal à ce plan. (Admis)
- En un point appartenant à un plan d'antisymétrie d'une distribution de courants, le champ magnétostatique appartient à ce plan. (Admis)
- Les propriétés pour les champs électrostatiques et magnétiques diffèrent : E est un "vrai" vecteur alors que B est un "pseudo" vecteur car défini à partir d'une convention mathématique d'orientation (celle du produit vectoriel).
Plans de symétrie ou d’antisymétrie des courants
Un plan est un plan de symétrie des sources du champ si elles restent inchangées lorsqu'on effectue la symétrie par rapport à ce plan.
Un plan est un plan d'antisymétrie des sources du champ si elles sont inversées (changement de signe pour les charges, de sens pour les courants) lorsqu'on effectue la symétrie par rapport à ce plan.
En tout point d'un plan de symétrie des sources, le champ électrique est contenu dans ce plan et le champ magnétique est orthogonal à ce plan.
En tout point d'un plan d'antisymétrie des sources, le champ magnétique est contenu dans ce plan et le champ électrique est orthogonal à ce plan.
Calculer un champ magnétique

Les méthodes sont numérotées par ordre de priorité.
Lorsqu'une action proposée est impossible, passer à la méthode suivante.
Méthode 1 : Théorème de superposition.
- Décomposer la distribution de courant en quelques distributions simples,
- Pour chaque distribution, calculer le champ magnétique au point M considéré en utilisant éventuellement les méthodes qui suivent,
- Additionner les champs en indiquant qu'il s'agit du théorème de superposition.
Attention :
- Les champs s'ajoutent en un même point M de l'espace,
- Il s'agit d'une somme vectorielle.
Rappel : somme vectorielle
Méthode 1 :
Utiliser la relation de Chasles en utilisant une notation intrinsèque pour les champs.
Méthode 2 :
- Déterminer la direction du champ total au point M :
- Méthode 1 : associer deux par deux des champs symétriques,
- Méthode 2 : trouver un plan de symétrie ou deux plans d'antisymétrie de la distribution de courants passant par M.
- Projeter les champs à additionner dans cette direction,
- Sommer ces différentes projections :
- Méthode 3 : Faire la somme des composantes dans une base orthonormée bien choisie,
- Méthode 4 : Somme graphique.
Méthode 2 : Théorème d'Ampère

- Déterminer l'allure du spectre dans tous l'espace d'étude :
- Déterminer la direction du champ en un point M quelconque de l'espace :
- Méthode 1 : associer deux par deux des champs élémentaires symétriques,
- Méthode 2 : trouver un plan de symétrie ou deux plans d'antisymétrie de la distribution de courants, passant par M.
- Déterminer les variables dont dépend la norme du champ dans l'espace, en évoquant des arguments d'invariance par translation ou rotation du problème vu par l'observateur,
- Choisir un contour d'Ampère passant par le point où on cherche le champ : Pour simplifier le calcul de la circulation, le contour doit suivre les lignes de champ ou les couper orthogonalement,
- Appliquer le théorème d'Ampère.
Méthode 3 : Calcul par intégrale
Pour avoir une méthodologie complète, je vous invite à vous diriger vers notre cours "Calcul d’Intégrales Multiples Vectorielles ou Scalaires".
Méthode 4 - Astuces
Pour une distribution de courant de type solénoïde infini, il faut admettre que le champ à l'extérieur du solénoïde est nul , puis utiliser le théorème d'Ampère.
Résumer avec l'IA :























Si vous désirez une aide personnalisée, contactez dès maintenant l’un de nos professeurs !