Chapitres
- 01. Introduction
- 02. Les différents types d'angles
- 03. Mesurer et tracer un angle
- 04. La bissectrice d'un angle
- 05. Les angles complémentaires, supplémentaires, adjacents et opposés par le sommet
- 06. Les angles alternes-internes et correspondants
- 07. Les angles dans les figures géométriques
- 08. Pour aller plus loin

Introduction
En géométrie, les angles sont partout. Ils permettent de tracer et d'identifier des figures particulières comme le triangle ou le carré mais ils permettent également de déterminer des longueurs dans ces figures. Ainsi, les angles sont la base de la géométrie.
Les différents types d'angles

Un angle est formé par deux demi-droites de même origine. L'origine, souvent noté O, est appelé le sommet de l'angle et les demi-droites sont appelées les côtés de l'angle. On mesure l'angle en degrés (noté °). Si A et B sont deux points des côtés respectifs de l'angle, on note l'angle  . De même, si les cotés de l'angle sont des demi-droites nommées (x) et (y), on note l'angle
. De même, si les cotés de l'angle sont des demi-droites nommées (x) et (y), on note l'angle 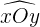 . Enfin, on peut noter l'angle
. Enfin, on peut noter l'angle 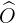 si c'est le seul angle d'origine O et qu'il n'y a pas d'ambiguïté.
si c'est le seul angle d'origine O et qu'il n'y a pas d'ambiguïté.
Il existe différents types d'angle :
- L'angle nul, qui mesure 0°.
- L'angle plat, qui mesure 180°.
- L'angle plein, qui mesure 360°.
- L'angle saillant, qui mesure entre 0° et 180°. Sa mesure est comprise entre celle de l'angle nul et celle de l'angle plat.
- L'angle rentrant, qui mesure entre 180° et 360°. Sa mesure est comprise entre celle de l'angle plat et celle de l'angle plein.
- L'angle droit, qui mesure 90°.
Deux droites qui se coupent en formant un angle droit sont dites perpendiculaires.
- L'angle aigu, qui mesure entre 0° et 90°. Sa mesure est comprise entre l'angle nul et l'angle droit.
- L'angle obtus, qui mesure entre 90° et 180°. Sa mesure est comprise entre l'angle droit et l'angle plat.
Les angles aigus et les angles obtus sont toujours des angles saillants.
Où trouver des cours de maths pour réviser avant une épreuve ?
Mesurer et tracer un angle
Différents instruments permettent de tracer ou mesurer un angle.
L'équerre est l'instrument qui permet d'identifier et de tracer les angles droits. En effet, elle possède tout simplement un angle droit à l'une de ses extrémités.
Souvent les équerres ont un angle droit et deux angles de 45° ou bien elles ont un angle droit, un angle de 60° et un de 30°.
Le rapporteur, quant à lui, permet de mesurer et de former différents angles.

Pour mesurer un angle, on place le centre du rapporteur (souvent représenté par un petit trou ou une croix) sur le sommet de l'angle et on fait en sorte que l'un des cotés de l'angle passe par l'une des graduations "0". Ainsi on compte le nombre de graduation à partir du "0" jusqu'à atteindre le second coté de l'angle.
Pour tracer un angle, on trace un segment  sur lequel on place le rapporteur de sorte que le centre du rapporteur soit sur le point A et que la graduation "0" soit sur le segment. On compte le nombre de graduation en partant du "0" et ce jusqu'à la mesure voulue. On marque au crayon un point C sur le bord du rapporteur indiquant la mesure voulue. Enfin on trace le segment
sur lequel on place le rapporteur de sorte que le centre du rapporteur soit sur le point A et que la graduation "0" soit sur le segment. On compte le nombre de graduation en partant du "0" et ce jusqu'à la mesure voulue. On marque au crayon un point C sur le bord du rapporteur indiquant la mesure voulue. Enfin on trace le segment  pour obtenir l'angle
pour obtenir l'angle 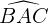 .
.
La bissectrice d'un angle
La bissectrice d'un angle est l'axe de symétrie de cet angle. En effet, c'est la demi-droite qui partage un angle en deux angles de même mesure. Les points appartenant à cette bissectrice sont équidistants des côtés de l'angle.
On peut construire la bissectrice d'un angle avec le rapporteur mais aussi avec un compas, de la façon suivante :
On veut tracer la bissectrice de l'angle  . On commence par tracer l'arc de cercle de centre O et passant par les points A et B. On trace ensuite deux arcs de cercles, de même rayon que le premier, mais cette fois de centre A pour l'un et de centre B pour l'autre. Ces deux arcs de cercles se coupent en un point M. Il ne reste qu'à tracer la droite passant par les points O et M : c'est la bissectrice de l'angle
. On commence par tracer l'arc de cercle de centre O et passant par les points A et B. On trace ensuite deux arcs de cercles, de même rayon que le premier, mais cette fois de centre A pour l'un et de centre B pour l'autre. Ces deux arcs de cercles se coupent en un point M. Il ne reste qu'à tracer la droite passant par les points O et M : c'est la bissectrice de l'angle  .
.
Les angles complémentaires, supplémentaires, adjacents et opposés par le sommet
Deux angles dont la somme des mesures vaut 90° sont dits complémentaires.
Deux angles dont la somme des mesures vaut 180° sont dits supplémentaires.
Deux angles ayant le même sommet, un côté commun et étant situé de part à d'autre de ce côté sont dits adjacents.
Deux angles symétriques par rapport à leur sommet commun sont dits opposés par le sommet. Ces deux angles ont la même mesure.
Les angles alternes-internes et correspondants

Les angles  et
et  sont alternes-internes par rapport aux droites (AB) et (CD) et la sécante (EK). Les angles
sont alternes-internes par rapport aux droites (AB) et (CD) et la sécante (EK). Les angles  et
et  sont correspondants.
sont correspondants.
Si les deux droites (AB) et (CD) sont parallèles alors les angles alternes-internes sont égaux. Inversement, si les angles alternes-internes sont égaux, les droites (AB) et (CD) sont parallèles. Cette propriété est aussi vraie pour les angles correspondants.
On en déduit donc : si la droite (EK) est perpendiculaire à la droite (AB) et à la droite (CD) alors les droites (AB) et (CD) sont parallèles. De même, si les droites (AB) et (CD) sont parallèles et que la droite (EK) est perpendiculaire à (AB) alors (CD) et (EK) sont perpendiculaires. De cette façon, tous les angles sont égaux : ce sont tous des angles droits.
Les angles dans les figures géométriques
Le triangle
Le triangle possède trois angles. La somme de ses angles fait toujours 180°. Les triangles particuliers ont d'autres propriétés sur leurs angles :
- Le triangle isocèle : ses angles à la base sont égaux.
- Le triangle équilatéral : chacun de ses angles mesure 60°.
- Le triangle rectangle : il possède un angle droit.
Le triangle rectangle a beaucoup de particularités. On dénote bien-sûr le théorème de Pythagore mais aussi des propriétés de trigonométrie qui permettent de déterminer les angles à partir des côtés et inversement : le cosinus, le sinus et la tangente.
Le cosinus de l'angle est le rapport des longueurs du côté adjacent à cet angle et de l'hypoténuse. Le sinus de l'angle est le rapport des longueurs du côté opposé à cet angle et de l'hypoténuse. Enfin, la tangente de l'angle est le rapport des longueurs du côté opposé à cet angle et du côté adjacent. Pour retenir ces formules, on utilise l'astuce mnémotechnique SOHCAHTOA (sinus=opposé/hypoténuse, cosinus=adjacent/hypoténuse, tangente=opposé/adjacent)
Par exemple, dans un triangle ABC rectangle en A, on veut déterminer l'angle B.

On a :
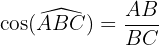
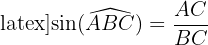
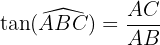
Le sinus et le cosinus d'un angle est compris entre 0 et 1. En effet, ils correspondent au rapport de deux longueurs positives et le dénominateur est la longueur du plus grand côté, l'hypoténuse. On a également les égalités suivantes :
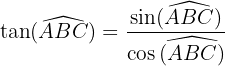 et
et 
Le quadrilatère
La somme des angles d'un quadrilatère est de 360°. Certains quadrilatères ont des angles particuliers :
- Le carré : tous ses angles sont droits et ses diagonales se coupent en formant un angle droit.
- Le rectangle : tous ses angles sont droits.
- Le losange : les angles opposés sont égaux et ses diagonales se coupent en formant un angle droit.
- Le parallélogramme : les angles opposés sont égaux.
Comment trouver des cours de maths seconde pour progresser ?
Pour aller plus loin
En mathématique, une autre unité de mesure existe pour la mesure d'un angle : c'est le radian. Par définition, 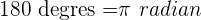 . Mais pourquoi utilise-t-on cette unité ?
. Mais pourquoi utilise-t-on cette unité ?
Quand on trace un cercle et que l'on trace un angle de sommet le centre du cercle, on observe que la longueur de l'arc de cercle, délimitée par les côtés de l'angle, est égale à la mesure de l'angle en radian. Ainsi, le radian permet de mesurer la longueur d'un arc de cercle. Le cercle a donc pour périmètre 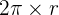 (avec r le rayon du cercle) puisque
(avec r le rayon du cercle) puisque 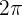 est la mesure de l'angle plein en radian.
est la mesure de l'angle plein en radian.
En trigonométrie, les angles sont orientés : l'angle est positif s'il est orienté dans le sens trigonométrique et négatif \sinon. Le sens trigonométrique est le sens inverse des aiguilles d'une montre. De cette façon, le sinus et le cosinus d'un angle est compris entre -1 et 1.
Résumer avec l'IA :























Si vous désirez une aide personnalisée, contactez dès maintenant l’un de nos professeurs !
Bonsoir je
suis trés heureux de voir vos différend cours. Merci beaucoup pour ce magnifique cours
Merci Diallo ! :)
bonjour j’ai vraiment aimé les détails de votre cours