Chapitres
Comme le rotationnel, le divergent ou encore le gradient, le laplacien est un opérateur mathématique qui permet de comprendre et d'étudier de nombreux domaines physiques comme l'électromagnétisme ou la mécanique des fluides.
On le retrouve décliné en coordonnées cartésiennes, polaires (2D), cylindriques (3D), sphériques (3D), mais aussi à la lumière de certaines interprétations physiques.
Sa forme varie donc selon le système de coordonnées, mais en général, laplacien mesure la somme des dérivées secondes d'une fonction, ce qui permet de fournir une information sur la courbure locale et sur la diffusion.
En géométrie, la divergence mesure comment un champ vectoriel se disperse ou converge en un point.
Et voici tout ce qu'il faut en savoir, point par point !

Le laplacien scalaire

L'opérateur laplacien est un opérateur différentiel qui associe à un champ scalaire la divergence de son gradient. Ainsi, cet opérateur renvoie un autre champ scalaire.
On le note :
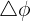
où phi est un champ scalaire.
On a :
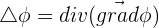

On peut également définir le laplacien comme l'opérateur nabla appliqué deux fois au champ.
Le laplacien d’une fonction mesure la différence entre la valeur de la fonction en un point et sa moyenne autour de ce point. C'est un opérateur de moyennage.
De cette façon, le laplacien est nul lorsque la moyenne autour d'un point vaut la valeur en ce point. Dans ce cas, on dit que la fonction est harmonique.
Le laplacien est un opérateur qui est linéaire et qui vérifie la règle de Leibniz pour un opérateur différentiel d'ordre deux.
On peut définir le laplacien en coordonnées cartésiennes. Soit f un fonction C² sur un ouvert de :
On définit le laplacien par :
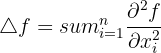
Avec une dimension, le laplacien d’un champ scalaire f(x) en un point est égal à la dérivée seconde du champ scalaire f(x) par rapport à la variable x en ce point. De cette façon, le laplacien indique la concavité.
La plupart du temps on se placera dans les cas bidimensionnel ou tridimensionnel.
En physique, seules les expressions en cartésiennes sont exigibles, un formulaire sera fourni pour les autres systèmes de coordonnées. Regardons malgré tout ce que cela nous donne.
Tout d'abord, regardons le cas bidimensionnel.
Soit f(x,y) le champ. On a pour coordonnées cartésiennes de paramètre (x, y, z) :
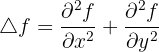
Pour les coordonnées polaires de paramètres, on a :
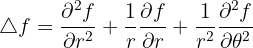
Passons au cas tridimensionnel.
Soit f(x,y,z) le champ. Les coordonnées cartésiennes de paramètres (x, y, z) nous donne :
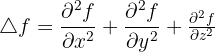
Avec les coordonnées cylindriques ayant pour paramètres (x=r cosθ, y=r sinθ, z), on obtient :
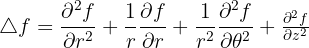
@mathpostbac #études #maths #pourtoi #espace #vectoriel ♬ son original - mathpostbac
Enfin, pour les coordonnées sphériques de paramètres (x=r sinθ cosΦ, sinθ sinΦ, r cosθ), cela nous donne :
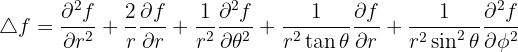
Le laplacien vectoriel

Le laplacien vectoriel est un opérateur différentiel qui s'applique à un champ vectoriel et qui renvoie un champ vectoriel.
Soit :
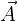
un champ vectoriel. On note son laplacien :
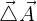
Il est définit par la relation :
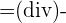
Dans un espace euclidien, on définit le plus souvent le laplacien vectoriel en utilisant des coordonnées cartésiennes.
Cela donne :
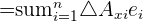 dans
dans 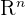
Dans un espace à trois dimensions, on a :
Où trouver des cours de maths pour réviser avant une épreuve ?
Applications en physique

Équation de Laplace
L'équation de Laplace consiste à résoudre 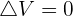 où V est un potentiel.
où V est un potentiel.
L'ensemble des fonctions vérifiant l'équation de Laplace sont dites harmoniques.
On retrouve cette équation notamment en thermodynamique, en électrostatique ou encore en mécanique des fluides.
Intéressons nous par exemple au cas de l'électrostatique. En se plaçant dans un espace de densité volumique de charge nulle, l'équation de Maxwell-Gauss devient :

En remplaçant :
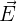
par son expression en fonction du potentiel électrique V, on obtient finalement :

qui correspond bien à l'équation de Laplace.
Si la densité de charge n'est pas nulle, nous n'obtenons pas l'équation de Laplace mais celle de Poisson, également définie grâce au laplacien :
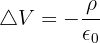
Équation de conservation
On retrouve le laplacien dans des équations de conservation. Il y apparait comme la divergence d’un flux. En effet, le flux est proportionnel au gradient d’une variable. C’est le cas par exemple dans l’équation de la chaleur :
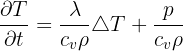
où T est la température, λ est la conductivité thermique, cv est la capacité thermique massique à volume constant, ρ est la masse volumique, p est la puissance volumique dégagée.
Équation d'onde

L'équation d'onde modélise la propagation d'une onde. Dans un milieu sans charge ni courant, où 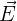 est un champ vectoriel, on a l'équation :
est un champ vectoriel, on a l'équation :
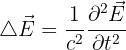
où c est la célérité et t le temps.
Si E est un champ vectoriel, en s'intéressant à chacune des composantes de :
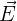
on obtient une équation sur un scalaire, appelé équation de d'Alembert :
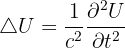
Équations de Navier-Stokes
En mécanique des fluides, on retrouve le laplacien dans différents cas. En effet, en étudiant les fluides newtoniens incompressibles, on utilise le laplacien.
Lorsque l'écoulement est irrotationnel, il existe une fonction Φ appelé le potentiel des vitesses telle que :
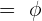
De cette façon :
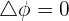
@docscifique Les équations de Navier-Stokes représentent l’un des sept problèmes du prix du millénaire, posés par l’Institut de mathématiques Clay. La résolution de ces équations, ou la démonstration de l’existence et de la régularité de leurs solutions, est un défi qui vaut un million de dollars et qui reste non résolu à ce jour. #science #mathematics #physics #CapCut #fypシ ♬ Solas x Interstellar - Gabriel Albuquerqüe
Pour un écoulement quelconque que l'on cherche à étudier, on utilise l'équation de Navier-Stokes qui utilise cette fois ci le laplacien des vitesses.
À présent, c'est à vous de jouer !
Résumer avec l'IA :























Si vous désirez une aide personnalisée, contactez dès maintenant l’un de nos professeurs !