Chapitres

Introduction et problématique du gradient
Le gradient est un concept mathématique fondamental permettant de généraliser la notion de dérivée aux fonctions de l'espace, c'est-à-dire les fonctions dépendant de plusieurs variables ( ).
).
En physique, de nombreuses fonctions sont des fonctions scalaires de l'espace et du temps, comme la pression  , la température
, la température 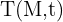 ou le potentiel électrique
ou le potentiel électrique 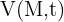 .
.
Le problème principal est de savoir comment représenter leurs variations spatiales locales (en un point donné  ).
).
Pour une fonction à une variable, la variation locale est représentée par la dérivée (la pente).
Pour une fonction à deux variables, la variation locale est représentée par les dérivées partielles (les pentes dans deux directions).
Pour une fonction à trois variables ou plus, la variation locale est représentée par le gradient.
Définition mathématique et propriétés du gradient
Le gradient d'une fonction scalaire  est noté
est noté 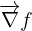 ou
ou 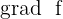 .
.
C'est un vecteur dont les composantes sont les dérivées partielles de la fonction par rapport à chaque variable.
C'est un vecteur dont les composantes sont les dérivées partielles de la fonction par rapport à chaque variable.
Lien entre gradient et différentielle totale
Le gradient est intimement lié à la différentielle totale 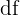 d'une fonction
d'une fonction 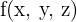 . La différentielle totale représente la variation élémentaire de la fonction
. La différentielle totale représente la variation élémentaire de la fonction  lors d'un petit déplacement
lors d'un petit déplacement 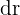 dans l'espace, de composantes
dans l'espace, de composantes 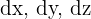 .
.
La différentielle totale s'écrit comme le produit scalaire du gradient par le vecteur déplacement élémentaire 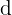 :
:
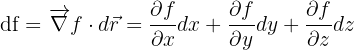

Propriétés du gradient
Direction : Le vecteur gradient 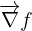 indique la direction dans laquelle la fonction
indique la direction dans laquelle la fonction  augmente le plus rapidement.
augmente le plus rapidement.
Norme : La norme du gradient 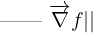 représente cette vitesse maximale d'augmentation.
représente cette vitesse maximale d'augmentation.
Lien avec les surfaces équi-valeur : Le gradient est toujours orthogonal (perpendiculaire) aux surfaces équi-valeur (ou iso-valeur) de la fonction  . Par exemple, le gradient de la température est perpendiculaire aux surfaces isothermes.
. Par exemple, le gradient de la température est perpendiculaire aux surfaces isothermes.
Expression du gradient dans les systèmes de coordonnées
Coordonnées cartésiennes
L'opérateur nabla (noté 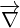 ) est un opérateur différentiel vectoriel. Le gradient d'une fonction
) est un opérateur différentiel vectoriel. Le gradient d'une fonction 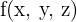 s'obtient en appliquant l'opérateur nabla à
s'obtient en appliquant l'opérateur nabla à  .
.
L'opérateur nabla en coordonnées cartésiennes est :
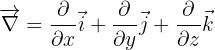
Le gradient de  est donc le vecteur :
est donc le vecteur :
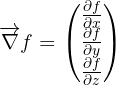
Il faut noter que pour effectuer les dérivées partielles, toutes les variables autres que celle par rapport à laquelle on dérive sont considérées comme des constantes.
Coordonnées cylindriques
En coordonnées cylindriques, un point  est caractérisé par
est caractérisé par  (rayon du cylindre),
(rayon du cylindre),  (angle polaire), et
(angle polaire), et  (coordonnée axiale).
(coordonnée axiale).
Le gradient d'une fonction 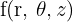 est :
est :
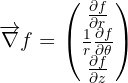
Coordonnées sphériques
En coordonnées sphériques, un point  est caractérisé par
est caractérisé par  (distance au centre),
(distance au centre),  (angle zénithal, entre l'axe
(angle zénithal, entre l'axe  et le rayon) et
et le rayon) et 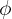 (angle azimutal, angle polaire).
(angle azimutal, angle polaire).
Le gradient d'une fonction  est :
est :
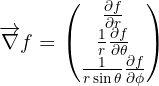
Représentation graphique des coordonnées
La représentation graphique des fonctions est possible tant que le nombre de variables n'excède pas trois.
En coordonnées cartésiennes ( ), on utilise les vecteurs unitaires
), on utilise les vecteurs unitaires 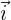 (abscisse),
(abscisse), 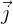 (ordonnée) et
(ordonnée) et 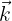 (profondeur).
(profondeur).
En coordonnées cylindriques, on utilise les vecteurs unitaires 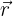 ,
, 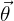 et
et 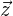 .
.
En coordonnées sphériques, on utilise les vecteurs unitaires 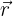 (distance au centre),
(distance au centre), 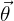 (angle zénithal) et
(angle zénithal) et 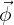 (angle azimutal).
(angle azimutal).

Exercices corrigés : calcul du gradient et de la différentielle totale
Exercice 1 : calcul en coordonnées cartésiennes
Soit  la fonction définie par
la fonction définie par  .
.
Calculer le gradient 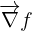 de la fonction
de la fonction  .
.
Calcul du gradient : on développe  .
.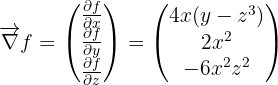
Déterminer la différentielle totale 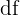 de la fonction.
de la fonction.
Calcul de la différence totale :
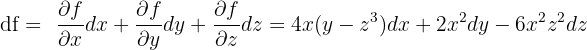
Exercice 2 : gradient d'une fonction à deux variables
Soit une fonction  définie par
définie par 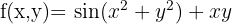 .
.
Déterminer les coordonnées du gradient 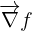 .
.
Calcul du gradient :
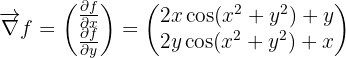
Calculer les coordonnées du gradient au point 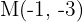 .
.
Calcul du gradient au point 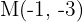 :
:
On a  .
.
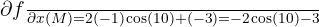

Calculer la valeur de la fonction au point 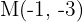 .
.
Valeur de la fonction au point 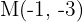 :
:
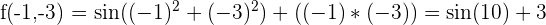
Déterminer la différentielle totale 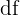 .
.
Calcul de la différentielle totale 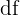 :
:























Si vous désirez une aide personnalisée, contactez dès maintenant l’un de nos professeurs !
Je suis vraiment fier de vous découvrir, votre blog est vraiment super ! J’aime bien son interface, et j’ai trop adoré le contenu aussi. Surtout continuez ainsi !
[url=http://www.qualite-voyance.fr]voyance par mail gratuite[/url]