Chapitres
- 01. Introduction
- 02. Définition
- 03. Propriétés
- 04. Le rotationnel en physique

Introduction
Définit grâce au gradient, le rotationnel est un outil mathématique utilisé notamment en électromagnétisme ou encore en mécanique des fluides. Avant de pouvoir l'appliquer en physique, étudions ces différentes propriétés mathématiques.
Définition

L'opérateur différentiel rotationnel est noté rot. Il s'applique à un champ de vecteurs et renvoie un autre champ de vecteurs.
Le rotationnel est définit comme le produit vectoriel du gradient par le champ de vecteurs.
Soit O un ouvert de 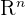 et V un champ de vecteurs sur O de classe
et V un champ de vecteurs sur O de classe 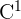
Alors le rotationnel de V est défini par 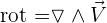 grâce à l'opérateur nabla.
grâce à l'opérateur nabla.
Lorsque le rotationnel d'un champ vectoriel est nul, on dit que ce champ est irrotationnel. Un champ irrotationnel dérive d'un potentiel.
C'est le cas par exemple du champ électrique qui dérive du potentiel électrique V en régime permanent ou encore du champ magnétique B qui dérive d'un potentiel scalaire magnétique en l'absence de courant.
Lorsque le rotationnel est non nul, on dit que le champ est tournoyant ou tourbillonnant. Le champ ainsi obtenu est perpendiculaire au plan du tourbillon.
La plupart du temps, on se placera sur un ouvert de  et on définira le rotationnel grâce aux coordonnées cartésiennes.
et on définira le rotationnel grâce aux coordonnées cartésiennes.
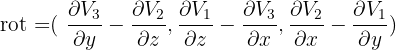
Le rotationnel, comme son nom l'indique, mesure la rotation d'un champ de vecteurs. De cette façon, un champ de vecteurs qui ne tourne pas aura un rotationnel nul.
On peut également définir le rotationnel dans d'autres systèmes de coordonnées comme en coordonnées sphériques ou cylindres mais sa définition est alors bien plus compliquée.
Seule l'expression en coordonnées cartésiennes est exigible, un formulaire sera fourni pour les autres systèmes de coordonnées si nécessaire.
Où trouver des cours de maths pour réviser avant une épreuve ?
Propriétés

Soient O un ouvert étoilé de  et V un champ de vecteurs de classe
et V un champ de vecteurs de classe 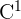 sur O.
sur O.
Un ouvert est dit étoilé par rapport à un point M0 de O si pour tout point M de O, le segment 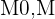 est entièrement contenu dans O. Ainsi, O est étoilé s'il existe un point M0 de O tel que O soit étoilé par rapport à M0.
est entièrement contenu dans O. Ainsi, O est étoilé s'il existe un point M0 de O tel que O soit étoilé par rapport à M0.
On a les identités suivantes :  où f est un champ scalaire, une application de classe
où f est un champ scalaire, une application de classe 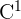
On a ensuite
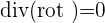 et
et 
De plus, l'opérateur rotationnel est linéaire.
Sur un ouvert étoilé, si un champ de vecteurs est de rotationnel nul, alors ce champ de vecteurs est un gradient.
Cela signifie que si rot V=0 dans O, alors il existe un champ scalaire f de classe 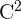 sur O tel que
sur O tel que  On appelle alors potentiel scalaire de V le champ scalaire f.
On appelle alors potentiel scalaire de V le champ scalaire f.
A l'inverse, si un champ de vecteurs est sans divergence sur un ouvert étoilé, alors ce champ de vecteurs est un rotationnel.

Enfin, terminons par le théorème de Stokes :
Soit dans O une surface S régulière, orientée et bornée dont la frontière 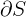 est constituée d'un nombre fini de courbes orientées. En supposant que les orientations de S et de sa frontière sont compatibles, on a
est constituée d'un nombre fini de courbes orientées. En supposant que les orientations de S et de sa frontière sont compatibles, on a 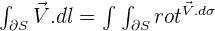
Cela revient à dire que la circulation de V le long du bord de S correspond au flux du rotationnel de V au travers de S.
Dans le cas particulier où S est contenu dans un plan, on appelle ce théorème le théorème de Green-Riemann. On considère ici que toutes les quantités sont donc définies sur 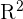
Énonçons précisément le théorème de Green-Riemann :
Soit O un ouvert de 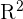 Soit dans O un ouvert B borné dont la frontière
Soit dans O un ouvert B borné dont la frontière 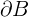 est entièrement contenue dans O et constituée d'un nombre fini de courbes orientées de façon directe par rapport à B. Soit V=(V1,V2) un champ de vecteurs de classe
est entièrement contenue dans O et constituée d'un nombre fini de courbes orientées de façon directe par rapport à B. Soit V=(V1,V2) un champ de vecteurs de classe 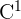 sur O alors
sur O alors 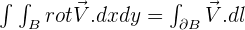
Le rotationnel en physique

Pour la définition du rotationnel, c'est le théorème de Stokes qui sera le plus utilisé en physique. Il est souvent plus élégant de calculer le rotationnel par analogie avec un champ connu dont on connait le rotationnel grâce à une loi physique.
Le rotationnel de la vitesse est visible en mécanique des fluides. Il permet de décrire une rotation de la particule de fluide. Si l'écoulement du fluide est irrotationnel, c'est à dire que le rotationnel est nul pour tout point, alors le vecteur vitesse est le gradient d'un écoulement potentiel.
On retrouve ce phénomène en électrostatique. L'équation de Maxwell-Faraday s'écrit en statique  De là, on peut définir le potentiel électrique, noté V, tel que
De là, on peut définir le potentiel électrique, noté V, tel que 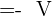
De manière plus générale, on retrouve le rotationnel en électromagnétisme où le champ électrique suit la loi d'induction de Maxwell-Faraday : 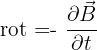 Cela signifie que la variation du champ magnétique
Cela signifie que la variation du champ magnétique 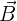 crée un champ électrique.
crée un champ électrique.
On le retrouve également dans l'équation de Maxwell-Ampère : 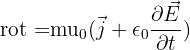 où
où 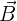 est un champ magnétique et j la distribution volumique de courants. Enfin,
est un champ magnétique et j la distribution volumique de courants. Enfin, 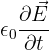 s'appelle le courant de déplacement.
s'appelle le courant de déplacement.
De plus, le rotationnel nous permet de définir le vecteur vorticité ou vecteur tourbillon qui correspond à la moitié du rotationnel de la vitesse du fluide, c'est à dire 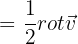 Le champ issu du rotationnel est perpendiculaire au plan du tourbillon, comme l'axe d'une toupie ou d'une tornade.
Le champ issu du rotationnel est perpendiculaire au plan du tourbillon, comme l'axe d'une toupie ou d'une tornade.
Résumer avec l'IA :























Si vous désirez une aide personnalisée, contactez dès maintenant l’un de nos professeurs !