Chapitres
Nous avons tous déjà entendu parler de cette petite puissance "²" présente en mathématiques et sur nos claviers d'ordinateur. Lorsque celle-ci apparait juste à droite d'un nombre, on dit que ce nombre est "au carré".
? Mais que signifie cette puissance ?
Les racines carrées sont une notion mathématique fondamentale. Une racine carrée d'un nombre est un autre nombre qui, lorsqu'il est multiplié par lui-même, donne le nombre d'origine.
? Par exemple, la racine carrée de 25 est 5, car 5 x 5 = 25
Les racines carrées sont généralement représentées par le symbole √. Les nombres négatifs n'ont pas de racines carrées réelles, mais ils ont des racines carrées imaginaires.
?? Les racines carrées sont utilisées dans de nombreux domaines, tels que la géométrie, l'algèbre, la physique et l'ingénierie. Il est important de noter que chaque nombre positif a deux racines carrées, une positive et une négative. Les racines carrées sont également essentielles pour résoudre des équations quadratiques et pour calculer des longueurs, des aires et des volumes dans la géométrie.

Le fonctionnement du carré d'un nombre ?

? Commençons par définir ce qu'est un nombre au carré. Lorsque l'on multiplie un nombre par lui même, on dit qu'on le met au carré. Par exemple, si on appelle "a" un nombre, on note 
Pourquoi utilise-t-on cette notation ? Lorsque l'on additionne un nombre plusieurs fois par lui même, par exemple :
$
On utilise la multiplication pour simplifier l'écriture
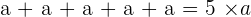
?♂️ De la même façon, les puissances nous permettent de simplifier les multiplications répétées :
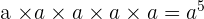
⚠️ Il est important de retenir que le carré d'un nombre est toujours positif
En effet, lorsque l'on multiplie deux nombres positifs entre eux on obtient un nombre positif, et il en est de même lorsque l'on multiplie entre eux deux nombres négatifs.
? Ainsi, la fonction carré est paire et admet un axe de symétrie qui est l'axe des ordonnées.

✅ La fonction carré associe à tout nombre réel x le nombre x² qui est à valeur dans l'intervalle 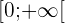 c'est à dire que la fonction renvoie uniquement des nombres positifs.
c'est à dire que la fonction renvoie uniquement des nombres positifs.
Cela implique également que :
- L'équation
 où a est un nombre négatif est impossible à résoudre
où a est un nombre négatif est impossible à résoudre - Il n'existe aucun nombre au carré qui est négatif
- Par contre, l'équation
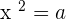 où a est positif admet deux solutions : une positive et une négative.
où a est positif admet deux solutions : une positive et une négative.
Par exemple :
L'équation  admet deux solutions : 4 et -4. En effet, (-4)²=4²=16.
admet deux solutions : 4 et -4. En effet, (-4)²=4²=16.
Par contre l'équation 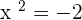 n'admet aucune solution, elle est impossible à résoudre
n'admet aucune solution, elle est impossible à résoudre
✍️ L'application réciproque de la fonction carré est la fonction racine carré. Elle associe à tout nombre x à valeur dans
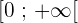 le nombre
le nombre 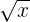
Cette fonction agit à l'inverse de la fonction carré. Par exemple :
- Comme 2² vaut 4 alors
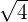 vaut 2
vaut 2 - Ainsi,
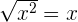
Un nombre entier qui est le carré d'un nombre est appelé "carré parfait". Par exemple, 9 est un carré parfait car 9 = 3².
? Le terme de carré à évidemment un lien avec la figure géométrique. En effet, l'aire du carré, polygone à 4 côtés de même longueur, est donc la longueur du côté au carré !
Les identités remarquables ⚠️

Il faut faire très attention lors de l'addition et de la soustraction de deux carrés.
En effet, soient a et b deux nombres, alors 
Pour additionner ou soustraire deux carrés, on utilise trois propriétés qu'il est nécessaire de connaître. On les appelle des identités remarquables.
Énonçons les et expliquons les avec des exemples.
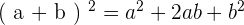
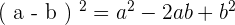

On appelle "forme factorisée" la partie de gauche dans chacune des identités et "forme développée" les parties à droite de l'égalité.
Calculons pour a=2 et b=3 :
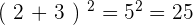
et
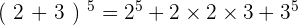
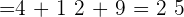
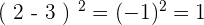
et
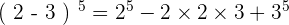
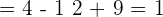

et

Multiplications et divisions de nombre au carré ?

La multiplication et la division de nombres au carré est bien plus simple que les additions et les soustractions.
En effet, soient a et b deux nombres, on a 
et

Prenons des exemples pour illustrer ces deux propriétés :

et
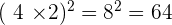
De même pour la division, 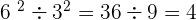
et
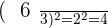
On pourrait également regarder ce que donne le carré d'un nombre au carré.

On découvre de cette façon la propriété nécessaire pour les calculs de puissances différentes ou non de la puissance de 2 !
Par exemple, 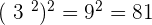
et
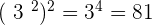
Table des nombres au carré ?

Les premiers carrés parfaits sont des nombres obtenus en multipliant un nombre par lui-même. Ils sont essentiels en géométrie pour le calcul des aires, en algèbre pour résoudre des équations quadratiques, en physique pour la cinématique, en informatique, en ingénierie, et en cryptographie, jouant un rôle fondamental dans une variété d'applications mathématiques et pratiques.
Comme on connaît les tables de multiplication, il est intéressant de connaître les premiers carrés.
? Résumons les dans un tableau :
| Nombre | Nombre au carré |
|---|---|
| -5 | (-5)²=25 |
| -4 | (-4)²=16 |
| -3 | (-3)²=9 |
| -2 | (-2)²=4 |
| -1 | (-1)²=1 |
| 0 | 0²=0 |
| 1 | 1²=1 |
| 2 | 2²=4 |
| 3 | 3²=9 |
| 4 | 4²=16 |
| 5 | 5²=25 |
| 6 | 6²=36 |
| 7 | 7²=49 |
| 8 | 8²=64 |
| 9 | 9²=81 |
| 10 | 10²=100 |
Exercices
Exercice 1
Résoudre les équations suivantes : x²=9; x²=0; x²=-3.
- La première équation nous donne x=3 ou x=-3. En effet, on sait que 3²=(-3)²=9.
- La deuxième équation a pour solution x=0. En effet, 0²=0 et c'est le seul nombre qui a pour carré 0.
- La dernière équation n'admet aucune solution. Il n'existe aucun carré négatif.
Exercice 2
Un fermier possède un champ qui forme un carré. Il mesure un des côtés et obtient 10m. Sachant qu'il peut mettre 1 vache tous les 10 mètres carré, combien de vaches peut il mettre dans son champ ?
Pour répondre à la question, il nous faut connaître l'aire du carré. L'aire vaut simplement la longueur du côté au carré :
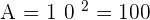
- Comme
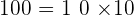 le fermier pourra mettre 10 vaches dans son champ.
le fermier pourra mettre 10 vaches dans son champ.
Exercice 3
Mettre les nombres suivants au carré : 3; -2; 0; -3; 5 et 9
Décrivons les résultats dans un tableau :
| Nombres de départ | Nombres au carré |
|---|---|
| 3 | 9 |
| -2 | 4 |
| 0 | 0 |
| -3 | 9 |
| 5 | 25 |
| 9 | 81 |
Exercice 4
Effectuez ou simplifiez les opérations suivantes :
- (3-1)(3+1)
- (x+4)²
- (4x)²
- 4² : 2²
Pour la première opération, on peut utiliser les identités remarquables :
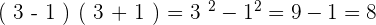
On utilise de la même façon la première identité remarquable pour la seconde opération :
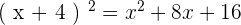
Pour le troisième calcul, on utilise les propriétés de la multiplication de deux nombres au carré :

Enfin, on applique la propriété de la division de deux nombres carré :
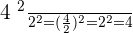























Si vous désirez une aide personnalisée, contactez dès maintenant l’un de nos professeurs !
Très bien ! Est-ce une propriété : la différence entre les différences de deux carrés de deux nombres entiers successifs est toujours de deux. Exemple : 6×6 = 36 ; 7 x 7 = 49 ; différence entre les deux carrés : 13 ; 7 x 7 =49 ; 8 x 8 = 64 ; différence entre les deux carrés = 15, soit différence de 2 avec la différence de 2 avec la différence précédente ???? (ETc….)
Bonjour ! Contactez nos professeurs de mathématiques sur Superprof, prêts à vous offrir un soutien personnalisé pour atteindre vos objectifs. Bonne journée !
Alors il existe les nombres complexe avec un carré négatif.. de rien.
Bonjour 👋 prof
J’ai du mal pour expliquer à ma petite fille qui a manqué le cours la solution de A2+5=?
Parfait
J’ai du mal pour expliquer à ma petite fille qui a manqué le cours la solution de A2+5=?
C’est très compréhensible
bravo
bravo