Chapitres
- 01. Les cônes de révolution
- 02. Les pyramides

Les cônes de révolution
Définition
Un cône de révolution de sommet S est un solide engendré par la rotation d'un triangle SOM, rectangle en O, autour de la droite (SO). La base du cône est un disque de centre O. La hauteur [SO] est perpendiculaire au plan de la base.

Propriétés
Le volume du cône de révolution se calcule de la manière suivante : V = (B · h)/3 avec V le volume du cône, B l'aire de la base et h la hauteur du cône. Par ailleurs l'aire de la base est égale à πR^2. En reprenant le cas de la figure ci-dessus, on obtient le volume du cône suivant : V = (π · OM^2 · OS)/3 Exemple : Volume d'un cône de hauteur h = 6 cm et de rayon de base r = 3 cm. V = (π·9·6)/3 = 18π V = 18π cm3 V ≈ 56,55 cm3
Patron
Pour déterminer le patron, il faut déterminer quelques longueurs car un cône est construit avec la base et la surface latérale. Reprenons le cas de l'exemple ci-dessus avec un cône de hauteur h = 5cm et de rayon de base r = 3cm. Pour la base du cône, il faut simplement construire un cercle de rayon r = 3cm. Pour déterminer le rayon de la surface latérale, il faut déterminer la longueur de l'hypoténuse du triangle, à savoir la longueur SM dans le cas de notre triangle dessiné. On utilise par conséquent le théorème de Pythagore pour déterminer la longueur de cette hypoténuse. D'après le théorème de Pythagore : SO² + OM² = SM² 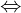 5² + 3² = SM²
5² + 3² = SM² 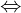 25 + 9 = SM²
25 + 9 = SM² 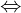 34 = SM²
34 = SM² 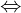 SM =
SM = 
 SM
SM 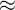 5.8cm. La valeur de SM correspond à la valeur de la surface latéral du cône de révolution. Enfin, pour déterminer l'angle de la portion de disque, on utilise un tableau de proportionnalité. On détermine dans un premier temps le périmètre de l'arc de cercle : P = 2πr = 6π. On a le tableau de proportionnalité suivant :
5.8cm. La valeur de SM correspond à la valeur de la surface latéral du cône de révolution. Enfin, pour déterminer l'angle de la portion de disque, on utilise un tableau de proportionnalité. On détermine dans un premier temps le périmètre de l'arc de cercle : P = 2πr = 6π. On a le tableau de proportionnalité suivant :
| Angle (en degrés) | 360 | x |
|---|---|---|
| Périmètre de l'arc de cercle | 10π | 6π |
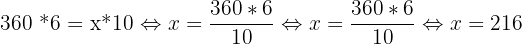 L'angle de portion est donc égal à 216 degrés. On a par conséquent toutes les informations pour pouvoir construire le patron de notre cône de révolution :
L'angle de portion est donc égal à 216 degrés. On a par conséquent toutes les informations pour pouvoir construire le patron de notre cône de révolution : 
Section
Il est possible de réaliser une section du cône de révolution. Cette section permettrait d'obtenir un nouveau cône plus petit que le précédent.
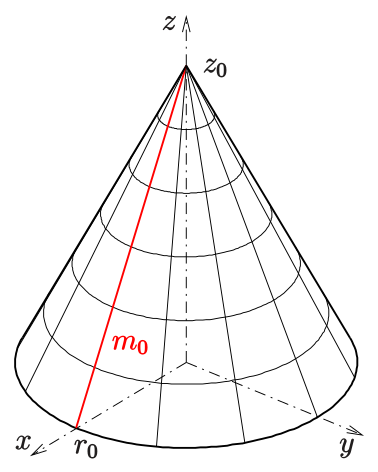
Le cône de révolution peut être sectionné pour former un nouveau cône de révolution plus petit. On peut dans ce cas, calculer facilement l'ensemble des différentes propriétés du cône via le coefficient de réduction. Pour cela, il suffit d'appliquer la formule suivante : Soit h la hauteur du cône de révolution initial, soit h' la hauteur du cône de révolution sectionné, on définit le coefficient du cône de révolution comme : 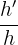 . Une fois ce coefficient de réduction obtenu, il reste simplement à appliquer ce coefficient sur l'ensemble des différentes propriétés. Besoin de cours de mathématiques ?
. Une fois ce coefficient de réduction obtenu, il reste simplement à appliquer ce coefficient sur l'ensemble des différentes propriétés. Besoin de cours de mathématiques ?
Les pyramides
Définition
Une pyramide est un solide composé de différentes figures géométriques associées :
- Une base représentant un polygone à n cotés (triangle, carré, pentagone, hexagone...)
- n faces latérales associées aux n cotés représentant pour chacune d'entre elles un triangle dont le sommet est commun et constitue le sommet de la pyramide
Comme pour le cône de révolution, on définit une pyramide par sa hauteur partant du sommet jusqu'à la base de la pyramide.
Propriétés
Le volume d'une pyramide se définit via la formule suivante : 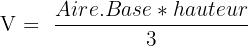 . Contrairement au cône de révolution, la formule permettant de calculer l'aire de la base varie selon le type de polygone à la base :
. Contrairement au cône de révolution, la formule permettant de calculer l'aire de la base varie selon le type de polygone à la base :
- Si la base de la pyramide est un triangle, on détermine l'aire via la formule A = (Base*Hauteur)/2
- Si la base de la pyramide est un carré, on détermine l'aire via la formule A = Coté*Coté
- Si la base de la pyramide est un pentagone, on détermine l'aire via la formule A = 5*(Base*Hauteur)/2
- Si la base de la pyramide est un hexagone, on détermine l'aire via la formule A = ((3√3)/2)*coté²
Au delà, les figures géométriques deviennent de plus complexes et par conséquent le calcul de l'aire du polygone se complexifie également.
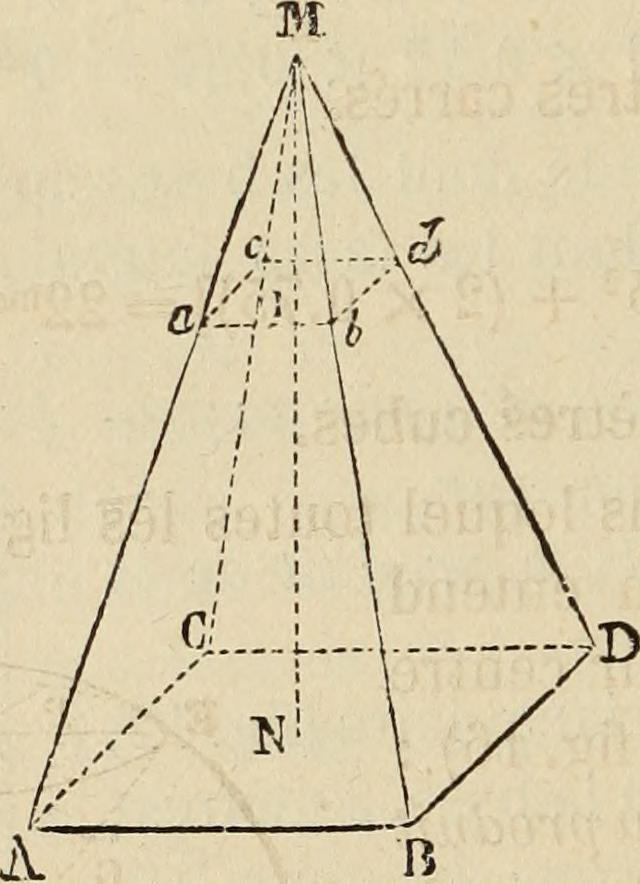
Par exemple, on souhaite calculer le volume de la pyramide ci-dessus. On sait que AC = 3cm et MN = 5cm. On calcule dans un premier temps l'aire du carré ABCD : Aire = coté*coté = AC² = 9cm². On sait que la hauteur de la pyramide correspond à la longueur MN. Il nous reste donc à calculer le volume directement : 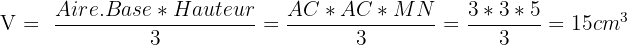
Patron
Pour construire le patron d'une pyramide, quel que soit le type de la pyramide, le concept est toujours identique. La base de la pyramide reste inchangé. Les différents triangles reliés aux sommets sont quant à eux tous rabattus. Quelque soit la base, le patron sera toujours en forme d'étoiles à n sommets avec n le nombre de cotés de la base.
Section
A l'instar du cône de révolution, il est possible de réaliser une section de la pyramide. Sur l'image ci-dessus, une pyramide sectionnée représenterait la pyramide Mabcd. On obtient alors la nouvelle hauteur avec la longueur MI. Pour connaitre les nouvelles volumétries de cette pyramide sectionnée, il faut simplement calculer le coefficient de réduction. Ce dernier se calcule via la division de la nouvelle hauteur par l'ancienne hauteur soit : 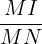 .
.
Comment demander de l'aide en cours de maths en ligne ?
Exercice
Soit un cube ABCDEFGH de côté 10cm dans lequel on découpe une pyramide ABCDE. On souhaite calculer le volume de cette pyramide et dessiner le patron. Pour calculer le volume, il nous faut connaitre deux élements : l'aire de la base ABCD et la hauteur AE. ABCDEFGH étant un cube, on sait que le quadrilatère ABCD est un carré. L'aire du carré est donc facile à calculer : 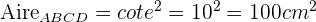 . Enfin, ABCDEFGH étant un cube, on sait que la hauteur AE = 10cm. Il ne nous reste plus qu'à appliquer la formule pour trouver la volumétrie :
. Enfin, ABCDEFGH étant un cube, on sait que la hauteur AE = 10cm. Il ne nous reste plus qu'à appliquer la formule pour trouver la volumétrie : 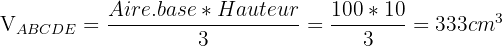 Pour pouvoir construire le patron, il faut connaitre l'ensemble des cotés de chaque triangle. Le coté AE est une hauteur, il est donc égal à 10cm. Pour déterminer le coté EB, on utilise le théorème de Pythagore. Le triangle EAB étant rectangle en A, d'après le théorème de Pythagore :
Pour pouvoir construire le patron, il faut connaitre l'ensemble des cotés de chaque triangle. Le coté AE est une hauteur, il est donc égal à 10cm. Pour déterminer le coté EB, on utilise le théorème de Pythagore. Le triangle EAB étant rectangle en A, d'après le théorème de Pythagore : 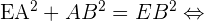
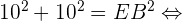

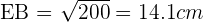 Le triangle EAD étant le même triangle rectangle, on sait que ED = 14.1cm. Enfin, dans le triangle EBC, on cherche à déterminer la valeur du coté EC. Le triangle EBC étant rectangle en B, d'après le théorème de Pythagore :
Le triangle EAD étant le même triangle rectangle, on sait que ED = 14.1cm. Enfin, dans le triangle EBC, on cherche à déterminer la valeur du coté EC. Le triangle EBC étant rectangle en B, d'après le théorème de Pythagore : 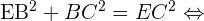
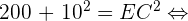

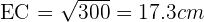 On a désormais l'ensemble des cotés menant au sommet du triangle. Il est par conséquent possible de construire le patron de la pyramide ABCDE avec les différentes distances adéquates.
On a désormais l'ensemble des cotés menant au sommet du triangle. Il est par conséquent possible de construire le patron de la pyramide ABCDE avec les différentes distances adéquates.
Résumer avec l'IA :






















Si vous désirez une aide personnalisée, contactez dès maintenant l’un de nos professeurs !
Au niveau du cône de révolution
L aire de la base (cercle ici ) c’est pi * r au carré
La formule 2*pi*r est la formule du périmètre du cercle dc tout le calcul qui en découle n’est pas bon
Dommage qu’il manque le patron !!
Sinon, une petite image pour illustrer ton document :
[img]http://mathematiques4.free.fr/images/solp4.jpg[/img]