Chapitres

Définition
La trigonométrie est une partie des mathématiques traitant des angles et des longueurs pour les triangles. Il traite également des différentes fonctions cosinus, sinus, et tangente.
Lien entre trigonométrie et triangle rectangle
La trigonométrie peut et s'utilise largement pour les triangles rectangles. Pour rappel, un triangle rectangle est un triangle contenant un angle droit (angle de 90 degrés). On définit sur un triangle rectangle, un côté adjacent, un côté opposé et une hypoténuse. L'hypoténuse est la plus simple à définir car il s'agit du côté le plus long, situé à l'opposé de l'angle droit. Les angles adjacents et opposés se définissent par rapport aux points du triangle. On voit les différents côtés du triangle comme suit :
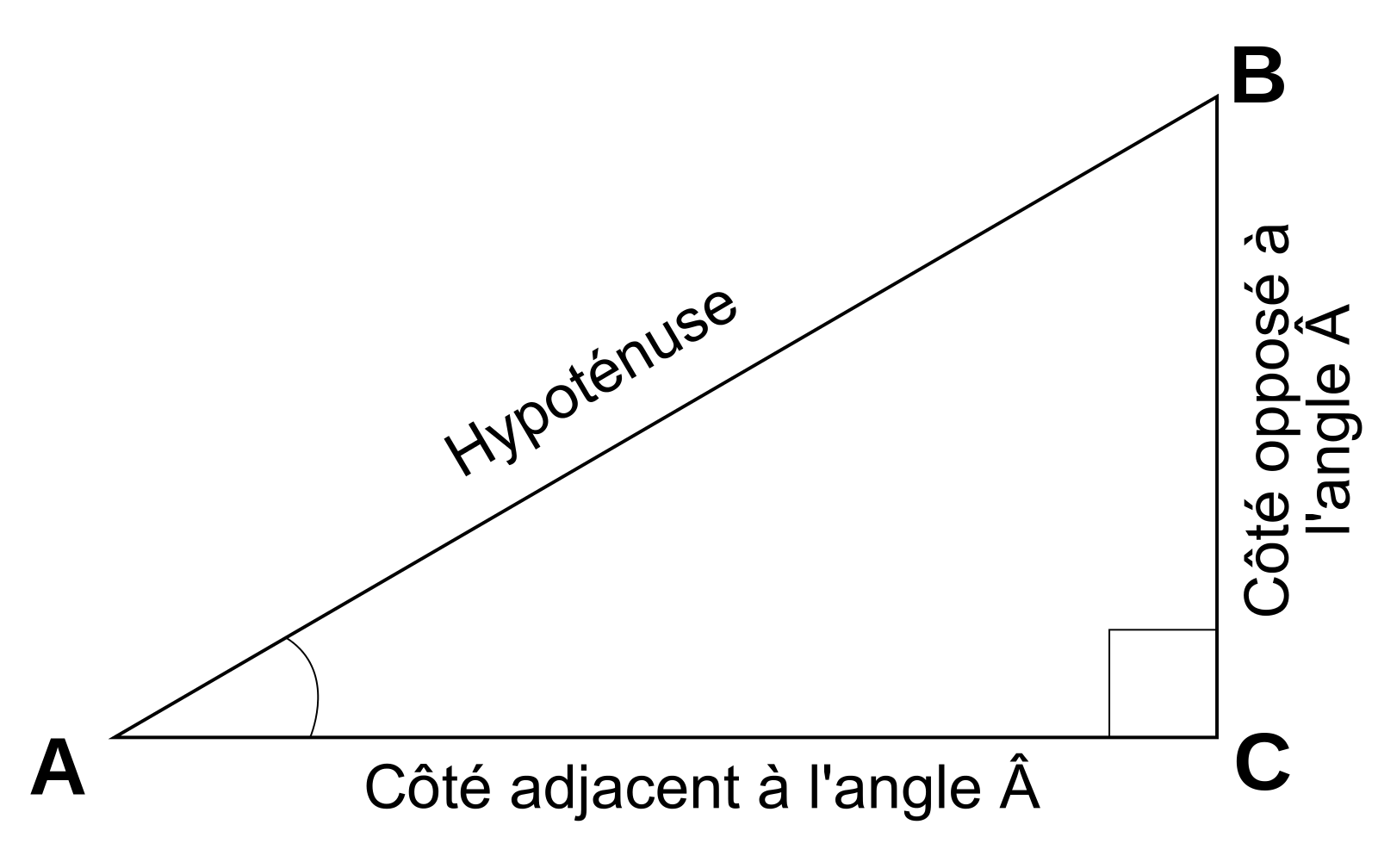
La trigonométrie permet de définir les relations suivantes :
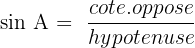 ;
; 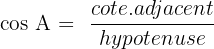 ;
; 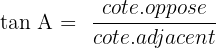
A noter qu'on peut désormais connaitre un côté du triangle avec seulement un coté et un angle donné contrairement au théorème de Pythagore qui nécessitait de connaitre à minima deux côtés du triangle.
Besoin de cours de math 3eme ?
Propriété de la trigonométrie
Les valeurs
La trigonométrie se repose sur trois fonctions : sin(x), cos(x), tan(x) avec x appartenant à R. Ces trois fonctions sont des fonctions cycliques et varient entre -1 et 1. La fonction tan(x) est un cas particulier, car elle se définit comme étant 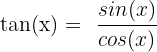 .
.
Pour déterminer les valeurs des fonctions sin(x) et cos(x), on utilise le cercle trigonométrique :

L'image ci-dessus étant très chargée, elle nécessite quelques explications. Nous allons expliquer point par point comment le cercle trigonométrique fonctionne :
- Un tour de cercle complet commence par le 0 à droite et tourne dans le sens inverse des aiguilles d'une montre.
- On dit que l'angle sous forme de π est en radian, tandis que la valeur en nombre entier est un degré. π radians équivaut à 180 degrés. Les divisions ou multiplications de π permettent de définir la transcription en radian ou en degré.
- Un tour de cercle complet est égal à 2π, un quart de cercle équivaut à π/2 et un demi cercle équivaut à π.
- La valeur du cosinus et sinus au delà d'un tour d'un cercle est identique. Par exemple, si on effectue un tour et un quart, cela équivaut à un tour de 5π/2. Cette valeur la est identique à la valeur π/2. On dit que les valeurs cosinus et sinus sont modulo 2π.
- La valeur du cosinus sur le cercle trigonométrique se définit sur l'axe des abscisses
- La valeur du sinus sur le cercle trigonométrique se définit sur l'axe des ordonnées.
- Les valeurs affichées entre parenthèses correspondent respectivement aux valeurs du cosinus et du sinus. Ces dernières correspondent à un angle donné définie par une valeur en radian.
- Quelque soit l'angle considéré, la valeur de cos(x) et sin(x) est toujours inférieure à 1
On peut consigner l'ensemble de ces valeurs remarquables dans un tableau :
| x | sin(x) | cos(x) | tan(x) |
|---|---|---|---|
| 0 | 0 | 1 | 0 |
| π/6 | √3/2 | 1/2 | √3/3 |
| π/4 | √2/2 | √2/2 | 1 |
| π/3 | 1/2 | √3/2 | √3 |
| π/2 | 0 | 1 | +/- ∞ |
A noter que les valeurs remarquables sont simplement calculées grâce à la propriété de la tangente disant que tan(x) = sin(x)/cos(x).
Où trouver des cours de maths pour réviser avant une épreuve ?
Inverse des fonctions
On peut calculer les valeurs inverses de sin(x), cos(x) et tan(x). Lorsque l'on doit par exemple résoudre la fonction : cos(x) = 1, il faut passer par la fonction inverse. Les fonctions inverses de ces fonctions sont respectivement arcsin(x), arccos(x) et arctan(x). En reprenant notre exemple précédent, on obtient alors :

Propriétés
En plus des différentes valeurs remarquables, les fonctions cosinus, sinus et tangente ont différentes formules remarquables.
| Type de formule | Formule |
|---|---|
| Identité remarquable | cos²(x) + sin²(x) = 1 |
| Addition | cos(x+y) = cos(x)cos(y)-sin(x)sin(y) |
| Addition | sin(x+y) = sin(x)cos(y) + cos(x)sin(y) |
| Addition | tan(x+y) = (tan(x) + tan(y))/(1-tan(x)tan(y)) |
Grâce aux formules présentes dans le tableau, nous pouvons également en déduire de nouvelles formules, à savoir :
cos(2x) = cos(x+x) = cos(x)cos(x) - sin(x)sin(x) = cos²(x) -sin²(x)
Or cos²(x) + sin²(x) = 1 d'où sin²(x) = 1 - cos²(x)
D'où cos(2x) = cos²(x) - sin²(x) = 2cos²(x) - 1 = 1 - 2sin²(x)
On peut faire de même pour sin(2x) :
sin(2x) = sin(x+x) = sin(x)cos(x) + sin(x)cos(x) = 2sin(x)cos(x)
Exercices corrigés
Exercices
Exercice 1 :
1. Déterminer à partir du triangle suivant, la valeur du cosinus, du sinus et de la tangente par rapport à l'angle α
2. On considère que b = 3, a = 4, h=5.
a. Vérifier que le triangle est effectivement un triangle rectangle.
b. Déterminer via le cosinus et le sinus la valeur de l'angle α.

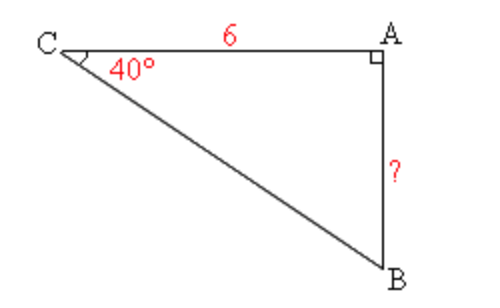
Exercice 2 : A partir du triangle ci-dessous, déterminer la valeur de la longueur AB :
Exercice 3 :
a. En sachant que cos(x) = 3/5, déterminer la valeur de sin(x) et de tan(x).
b. Soit un triangle ABC rectangle en A et α l'angle ABC. On sait que la valeur sin(x) est égale à 1/6. Déterminer la valeur de cos(x) et de tan(x).
Exercice 4 : En reprenant la figure de l'exercice 1, déterminer la valeur de a et b en sachant que l'angle alpha est égal à 20 degrés et que l'hypoténuse h est égale à 6.
Corrigés
Exercice 1 :
1. On détermine les différentes valeurs :
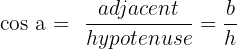 ;
; 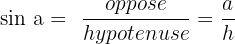 ;
; 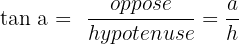
2.a. Pour déterminer si le triangle est un triangle rectangle, on utilise la réciproque du théorème de Pythagore :
h² = 5² = 25
a² + b² = 3² + 4² = 9 + 16 = 25
D'où h² = a² + b²
D'après la réciproque du théorème de Pythagore, le triangle est un triangle rectangle.
2.b. A partir des valeurs données,
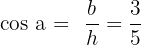 ;
; 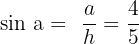
Exercice 2 : On a la mesure de l'angle C. Le coté adjacent représente par conséquent le coté AC, le côté opposé représente le côté AB et l'hypoténuse représente le coté BC.
Les cotés qui nous intéressent ici sont les côtés CA et AB à savoir le coté adjacent et le côté opposé. On doit donc utiliser la tangente :
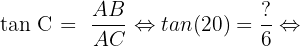
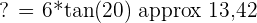
Le côté AB est donc environ égal à 13,42.
Exercice 3 :
a. Pour déterminer la valeur de sin(x) à partir de cos(x), on peut utiliser la formule suivante :


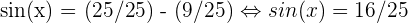
Il reste simplement à calculer la racine :
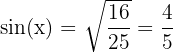
Il nous reste désormais à déterminer tan(x). Or on sait que :
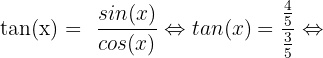
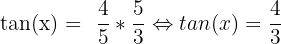
On obtient donc 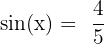 et
et 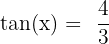
b. Comme précédemment, on va appliquer nos formules de trigonométrie pour déterminer le résultat. On va donc dans un premier temps déterminer la valeur de cos(x).
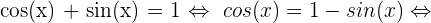
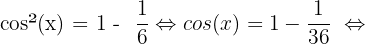
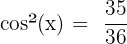
D'ou 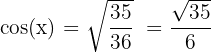
Enfin, pour calculer la valeur de la tangente, on utilise la formule suivante :
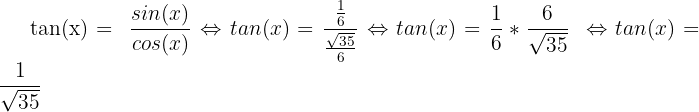
Exercice 4 :
Avec les informations que l'on a, on connait l'angle alpha et la valeur de l'hypoténuse. On pourra ainsi trouver respectivement la valeur du côté adjacent et du côté opposé avec le cosinus et le sinus.
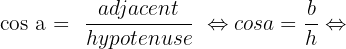
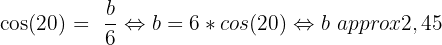
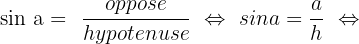
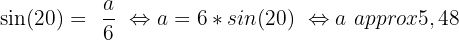























Si vous désirez une aide personnalisée, contactez dès maintenant l’un de nos professeurs !
Il faut préciser que les angles sont en radian et pas en degrès, aussi la formule cos(a)+sin(a)=1 est fausse puisque c’est cos(a)^2+sin(a)^2=1 et a l’exercice numéro 2 c’est tan(40) pas tan(20
J’ai bcp aime