Chapitres

Théorème de Pythagore
Dans un triangle rectangle, le carré de l'hypoténuse est égal à la somme des carrés des deux autres côtés.
Si ABC est rectangle en A, alors
Dans un triangle rectangle, l'aire du carré vert est égale à la somme des aires des carrés bleus et jaunes.
Le théorème de Pythagore sert à calculer des longueurs dans un triangle rectangle.
Calcul de la longueur de l'hypoténuse dans un triangle rectangle
En cour de math, ABC est un triangle rectangle en A. Donc, d'après le théorème de Pythagore,
=
Donc = 100 + 25
= 125
donc BC = cm ( c'est la valeur exacte)
donc BC
Calcul de la longueur d'un côté de l'angle droit dans un triangle rectangle
Dans ABC rectangle en A, on sait que BC = 10 cm et AC = 5 cm. Calculer AB. En donner la valeur arrondie au mm.
ABC est un triangle rectangle en A. Donc, d'après le théorème de Pythagore,=
Donc 100 = + 25
donc = 100 - 25
= 75
AB =
Calcul de la longueur de l'hypoténuse dans un triangle rectangle
En cour de math, ABC est un triangle rectangle en A. Donc, d'après le théorème de Pythagore,
=
Donc = 100 + 25
= 125
donc BC = cm ( c'est la valeur exacte)
donc BC
Réciproque du théorème de Pythagore
Comment prouver qu'un triangle est un triangle rectangle ?
ABC est un triangle tel que AB = 4 cm, AC = 3 cm et BC = 5 cm. ABC est-il un triangle rectangle ?
= 16 + 9 = 25
= 25
Donc =
Donc ABC est un trinagle rectangle en A d'après la réciproque du théorème de Pythagore.
Si dans un triangle le carré du côté le plus long est égal à la somme des carrés des deux autres côtés, alors ce triangle est un triangle rectangle.
Si, alors ABC est un triangle rectangle en A.
La réciproque du théorème de Pythagore sert à prouver qu'un triangle est un triangle rectangle.
Attention : Il faut calculer séparément le carré du côté le plus long et la somme des carrés des deux autres côtés.
De plus il faut comparer les valeurs exactes de ces deux nombres. On ne peut pas prouver une égalité en utilisant des valeurs approchées !
Comment suivre des cours de maths en ligne ?
BIOGRAPHIE
Pythagore (en grec Πυθαγόρας / Pythagóras, annoncé par la « Pythie »), né vers -580 et mort vers -490, était un mathématicien, philosophe et astronome de la Grèce antique.
Pythagore, fils du Phénicien Mnésarchos, serait né à Samos, une île des Sporades protégée par Héra, la déesse au paon (ou à Tyrrhénie, ou à Tyr, ou en Syrie, cf. Clément d'Alexandrie, Stromates, I, 62) vers -580 et serait mort vers -490 ou -497, à plus de quatre-vingt ans (son acmé se situe dans la 60e olympiade, 540–537, selon Diogène Laërce).
Contre toute évidence chronologique (un siècle d'écart), la tradition romaine en faisait le maître de Numa Pompilius, deuxième roi légendaire de Rome et le tenait pour fondateur de la religion romaine. L'historien Tite-Live réfute cette thèse dans son Histoire romaine I-18.
Le nom de son père nous est donné par Hérodote dans le seul passage où il parle de Pythagore (Enquête, IV, 95) : Zalmoxis, la divinité thrace, fut en réalité un homme esclave de Samos « au service de Pythagore, fils de Mnésarchos ». Son père, graveur de pierres précieuses, et sa mère Parthenis, la plus belle des Samiennes, descendaient tous deux du héros Ancée, fils de Zeus, qui avait fondé la ville de Samos. Mnésarchos et Parthenis s'étant rendus à Delphes pour consulter la Pythie, ils apprirent que Parthenis était enceinte et mettrait au monde un fils beau et sage ; Mnésarchos changea alors le nom de sa femme en Pythaïs (la « Pythienne »), et nomma l'enfant annoncé par la Pythie « Pythagore », l'« annonciateur pythien ». En réalité, si Pythagore avait hérité de son père charnel un corps sujet à la naissance et à la mort, il tenait son nous, la partie hégémonique de son âme, d'Apollon lui même dont Pythaïs aurait eu les faveurs.
L'enfant sera confié aux meilleurs maîtres. Hermodamas (Diogène Laërce), neveu de Créophyle de Samos, qui avait été l'hôte d'Homère, lui apprit L'Iliade et L'Odyssée par coeur.
Il suivit ensuite les enseignements de Phérécyde de Syros, duquel il était le neveu par sa mère, et qui lui enseignait dans une caverne. Pour Cicéron (Tusc., I, 16) Phérécyde aurait été le premier à soutenir que les âmes des hommes sont immortelles, ce qui l'influencera profondément. Selon Dicéarque (Porphyre Vie de Pythagore, 11) Pythagore aurait assisté aux derniers moments de Phérécyde, et selon Aristoxène (Diogène Laërce, Vies, I, 118), il l'aurait enterré à Délos.
Thalès de Milet lui aurait enseigné la maîtrise du temps, la tempérance et la science véritable. Il aurait enfin connu Anaximandre, dans la même cité.
Après avoir quitté Milet, Pythagore se rendit à Sidon, en Phénicie où il rencontra les descendants du prophète Môkhos qui l'initièrent aux Mystères à Tyr et à Byblos. Faisant retraite dans le temple du Mont Carmel, la montagne du Seigneur Élie, il accomplit son premier miracle en franchissant un précipice de la montagne pour rejoindre un navire au pieds de la montagne, qui le mènera en Égypte.
Reçu à Saïs par le pharaon Amasis, il passera vingt-deux ans dans ce pays où il sera initié aux Mystère de Diospolis (Thèbes) et à la doctrine de la résurrection d'Osiris ; les prêtres lui auraient appliqué sur la cuisse le disque ailé d'Atoum-Râ, en feuille d'or, ce qui lui vaudra le surnom de Pythagore chrysomère, i.e. "à la cuisse d'or".
Prisonnier de Cambyse lors de la conquête de l'Egypte, en -525, Pythagore sera conduit en Chaldée où il apprendra des Mages, durant douze années, la doctrine des nombres et la musique.
Il fut peut-être également en relation avec le chaldéen Zaratas-Zoroastre qui l'aurait purifié de ses souillures (Hippolyte, Réfutations de toutes les hérésies, I, II, 12). Il aurait vécu dix ans en Perse après la chute de l'imposteur Smerdis. Il aurait même été jusqu'en Inde où il aurait rencontré le Bouddha.
Libéré de Perse par un Crotoniate du nom de Gillos, selon Apulée, Pythagore revient à Samos où le tyran Polycrate régnait toujours. Il commence à enseigner dans un amphithéâtre à ciel ouvert, l'Hémicycle, sans grand succès.
Selon une tradition, avant de devenir célèbre pour son enseignement philosophique, Pythagore participa aux Jeux Olympiques à l'âge de 18 ans. Il remporta toutes les compétitions de pugilat[1] (sport de l'Antiquité comparable à la boxe)
Banni par Polycrate ou bien quittant Samos de son plein gré, il part pour la Grande Grèce et s'installe à Crotone où il restera une vingtaine d'années. Son influence sur Crotone s'étendit de l'assemblée aux enfants en passant par les adolescents et les femmes qui venaient tous l'écouter. Mais son enseignement était soumis à une règle de silence. Il fonda son école à Crotone.
Cette influence à Crotone est l'occasion pour Porphyre de Tyr d'écrire une description sans doute idéalisée et romancée de Pythagore :
« (…) les habitants de Crotone comprirent qu'ils avaient affaire à un homme qui avait beaucoup voyagé, un homme exceptionnel, qui tenait de la fortune de nombreux avantages physiques : il était en effet noble et élancé d'allure et, de sa voix, de son caractère et de tout le reste de sa personne émanaient une grâce et une beauté infinies. »
Il semble que Pythagore ait également introduit de nombreux rituels importés d'Égypte, et qu'il acquit ainsi une grande renommée : les habitants de Crotone l'appelèrent Apollon Hyperboréen.
Pythagore semble avoir eu deux enfants de Théano, pythonisse originaire de Crète : Arimnestos (qui fut peut-être le maître de Démocrite, cf. Porphyre de Tyr, Vie de Pythagore, 3), ou Télaugès, et une fille du nom de Mya (ou Arignotès). Il semble que ses enfants aient écrit des traités. D'après Timée de Locres (ibid., 4), cette fille était honorée « comme la Vierge des vierges et comme la Femme des femmes » et, après sa mort, sa maison devint pour les habitants de Crotone un sanctuaire de Déméter.
Prêt pour des cours de math 3eme ?
Outre la fondation de l'école pythagoricienne, il serait à l'origine de la gamme musicale fondée sur le « cycle des quintes », et lui a donné son nom. Selon Isocrate (Busiris, 28–29), c'est lui qui introduisit la philosophie en Grèce, et qui inventa ce mot.
Il aurait également introduit les mesures et les poids. Pythagore étudia les sciences mathématiques qu'il a appris des Égyptiens, des Chaldéens (astronomie) et des Phéniciens (nombres et calculs arithmétiques).
Il aurait également appris l'art de faiseurs de miracles de Phérécyde. On rapporte d'ailleurs de nombreuses légendes sur son compte, faisant état de ses dons d'ubiquité, de sa jambe en or, etc. Ce caractère légendaire de la vie de Pythagore, qui suggère parfois l'usage d'artifices en vue de séduire, se retrouve également dans son entourage. En effet, l'un de ses anciens esclaves, Zalmoxis (Salmoxis), passe pour avoir dupé ses concitoyens en tirant profit de la sagesse de Pythagore : il leur enseigna la doctrine de l'immortalité de l'âme, puis il se cacha dans un souterrain pendant trois ans en se faisant passer pour mort. Il réapparut, au grand étonnement de tous, et, dès lors, sa parole devint l'objet d'une véritable foi.
Vers la fin de sa vie, Pythagore s'enfuit pour Métaponte à la suite d'un complot fomenté en son absence contre lui et tous les pythagoriciens dont certains furent brûlés vifs dans une maison par les hommes d'un noble de Crotone, Cylon. Ce dernier voulait ainsi se venger du vieux Pythagore qui l'avait jugé inapte à suivre les enseignements de l'école. Ces persécutions conduisirent à la dispersion des membres de l'école pythagoricienne, et marquent le commencement du déclin de l'influence pythagoricienne en Italie, dont le dernier bastion fut Tarente, avec Archytas de Tarente.
Pythagore serait mort à Métaponte, où il fut enterré, à l'âge de 90 ans.
Son influence a été très grande : Empédocle aurait été l'un de ses disciples (ce point est toutefois réfuté par la chronologie), et Démocrite admirait sa pensée.
Les compagnons identifiaient Pythagore comme l'une de leurs références, notamment en raison de la rigueur de l'enseignement, du caractère scientifique, mathématique, communautariste.
Résumer avec l'IA :
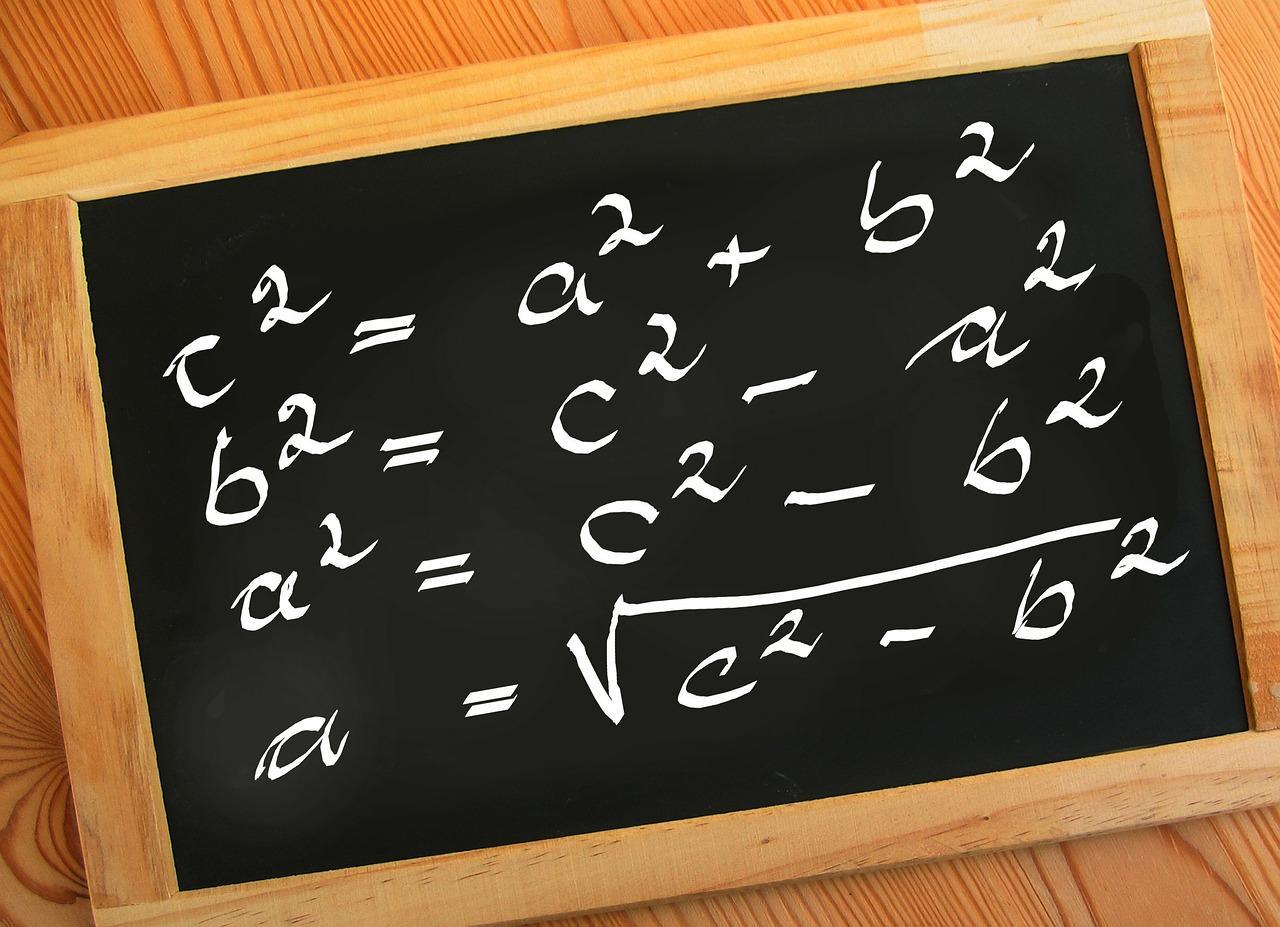






















Si vous désirez une aide personnalisée, contactez dès maintenant l’un de nos professeurs !