Chapitres

Prérequis : système étudié et référentiel
La description du mouvement et de la trajectoire d’un objet ne sera pas la même selon le référentiel d’étude. Prenons l’exemple d’une balle, qui constitue le système étudié, posée sur une planche à roulettes en mouvement. Selon le référentiel, le mouvement de la balle diffère.
Il est important de toujours préciser le système étudié, qui correspond à l’objet dont on analyse le mouvement, et le référentiel. Un référentiel est, le plus souvent, le solide par rapport auquel le mouvement du système sera étudié, selon un repère d’espace. Ce repère sera le plus souvent cartésien et orthonormé.
Newton s'est basé sur une analogie connue dans l'Antiquité (la loi en carré inverse).
Aujourd'hui, grâce à la relativité, nous savons que les ondes gravitationnelles présentent de nombreuses analogies avec les ondes électromagnétiques, mais ce n'était pas aussi évident à l'époque (ps : merci @Uriel_Kerzu pour le correctif).
Expression de la force de gravitation
C'est en 1687 qu'Isaac Newton révéla, dans un ouvrage intitulé Principes mathématiques de la philosophie naturelle, les résultats de ses recherches sur la gravitation, marquées par ses (supposées) comparaisons entre la chute d’une pomme et le mouvement de la Lune autour de la Terre.
Alors qu’il observe la Lune, il constate que la pomme, quand elle n’est plus retenue par une branche, tombe sur le sol. Selon lui, ces deux phénomènes sont liés au même principe physique : la gravitation.
Newton établit que tous les corps possédant une masse exercent l’un sur l’autre une force équivalente qui les attire l’un vers l’autre, appelée force de gravitation, et propose une relation qui permet de calculer la valeur de cette force. Elle est valable en tout point de l’espace.

Si un corps A et un corps B ponctuels possèdent respectivement une masse mA et une masse mB et sont séparés par une distance d, alors la valeur F de la force de gravitation qui s'exerce entre eux est :
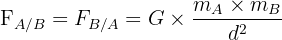
Dans cette formule, on a :
- Les masses mA et mB exprimés en kg
- La distance d exprimé en m
- La constante de gravitation G égale à G = 6,67 x 10-11m2.kg-2
Remarques :
- Cette loi est universelle. Elle s’exerce sur tous les objets, à partir du moment où ces derniers possèdent une masse.
- F correspond aussi bien à la valeur de la force exercée par le corps A sur le corps B que celle de la force exercée par le corps B sur le corps A. Ces forces ont la même direction, un sens opposé et une même valeur F.
- Cette expression est aussi valable pour des corps non ponctuels : dans ce cas, "d" représente la distance entre les centres d'inertie des deux corps.
Les facteurs qui influencent la force de gravitation
La force de gravitation est exprimée en fonction de trois grandeurs : G, les masses des corps et leur distance.
- G est une constante universelle et sa valeur reste donc toujours la même. Elle ne peut donc modifier la valeur de la force de gravitation.
- Les masses : La force de gravitation est proportionnelle aux masses des corps qui interagissent. Par exemple, un corps ayant une masse deux fois plus importante correspond à une force deux fois plus grande.
- La distance : La force de gravitation est inversement proportionnelle au carré de la distance qui sépare les corps. La force diminue donc si la distance augmente. Si, par exemple, on double la distance, la force F est divisée par quatre (22). Si l'on triple la distance F est divisée par neuf (32), etc.
La constante de gravitation
La loi de gravitation s’applique entre tous objets possédant une masse. En ce moment même, par exemple, elle s’applique entre vous et le support sur lequel vous lisez cet article (que ce soit un ordinateur ou un téléphone). Vous n’en ressentez cependant pas les effets à cause de la constante de gravitation G d’une valeur relativement faible. À une aussi faible distance, les masses des corps impliqués dans la force doivent être très importants afin que la force soit suffisamment importante pour ressentir quelque chose.
La constante de gravitation G correspond à la force entre deux masses d’un kilogramme chacune, séparées par une distance d’un mètre. En utilisant les unités du système international, cela correspond à la valeur suivante :
G = 6,67408 x 10-11 m3.kg-1.s-2
L’utilisation de ces unités s’explique par le fait que la constante relie une force, qui s’exprime en newton (N), à des masses exprimées en kg et une distance exprimée en mètre. Or, le newton caractérise une force colinéaire à un mouvement qui, appliquée à un objet d’un kilogramme, est capable de modifier sa vitesse d’un mètre par seconde. Un newton équivaut donc à 1 kg.m.s-2. En réalisant une analyse dimensionnelle (méthode permettant de vérifier l’unité d’un résultat lors d’un calcul mettant en jeu plusieurs unités) sur la loi de la gravitation universelle, on peut déduire l’unité de la constante de gravitation en utilisant le newton. On obtient alors la valeur simplifiée suivante :
G = 6,67 x 10-11 N.m2.kg-2
Utilisations de la loi de la gravitation universelle
Notion de gravité
La loi de la gravitation permet donc de calculer une force s’exerçant entre deux objets. Dans un référentiel terrestre, on peut alors calculer la force s’exerçant entre la Terre et nous. En utilisant la formule précédemment décrite, avec un humain pesant environ 50 kg, une masse terrestre environ équivalente à 5,95 x 1024 kg et une distance entre le centre de la Terre et le centre de gravité de l’humain considéré d’environ 6371 km (soit le rayon de la Terre), on obtient une force approximativement égale à 500 N. Cette force correspond ici plus généralement à ce qu’on appelle la gravité : c’est cette force qui nous retient sur Terre.
Cependant, la loi de la gravitation explique que deux objets exercent la même force l’un sur l’autre. En sautant dans le vide, la Terre devrait donc être attirée par nous de la même façon que nous sommes attirés vers elle lors de notre chute. Cela ne se produit pas à cause de la très grande différence de masse : la Terre ayant une masse beaucoup plus importante qu’un humain, elle sera de fait beaucoup plus difficile à mettre en mouvement. C’est ce phénomène qui explique, qu’à force équivalente, un coup dans un ballon de football n’aura pas le même impact qu’un coup dans une balle de bowling.
Au voisinage de la Terre, comme dans le cas précédemment décrit d’un humain marchant sur le sol terrestre, la formule de la loi de gravitation est équivalente à celle du poids. Le poids est donc un cas particulier de la loi de la gravitation universelle : il résulte de l’interaction gravitationnelle entre chacun de nos atomes et chacun des atomes de la Terre. Bien que ces forces soient très faibles, un effet cumulatif crée une force macroscopique : le poids.
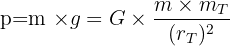
Dans cette formule :
- p correspond au poids, force de la pesanteur exercée par la Terre sur un corps dans son voisinage, et dirigée vers le centre de la Terre. Le poids s’exprime en N.
- m correspond à la masse de l’objet considéré (l’humain dans notre exemple), exprimée en kg, alors que mT correspond à la masse de la Terre, environ équivalente à 5,95 x 1024
- g correspond à l’accélération de la pesanteur, égale à 9,80665 m.s-2, soit approximativement 9,81 N.kg-1. Cette valeur n’est pas égale en tout point de la Terre.
Le poids est donc dépendant de la gravitation terrestre. Il ne faut donc pas le confondre avec la masse, comme cela est souvent fait dans le langage courant. Le poids d’un objet ne sera pas le même sur la Lune ou sur la Terre, alors que la masse sera inchangée quel que soit l’environnement.
La gravitation et les planètes
Prenons maintenant l’exemple d’un objet lâché sur le sol terrestre. Sans vitesse initiale, cet objet tombera sur le sol. Cependant, si on applique une autre force sur cet objet, en le lançant dans une direction par exemple, avec une certaine vitesse, l’objet va alors tomber tout en se dirigeant dans la direction dans laquelle il a été lancé. Plus la vitesse de lancer sera importante, plus l’objet se déplacera dans la direction du lancer (avec une distance parcourue de plus en plus importante), selon une trajectoire parabolique tout en retombant vers le sol. Maintenant, s’il était possible de lancer l’objet avec une vitesse élevée (à partir d’une hauteur importante), l’attraction de l’objet pour le sol serait compensée par la vitesse : ce dernier ne tomberait donc pas sur le sol, mais entrerait en gravitation autour de la Terre.
C’est la réflexion qu’a eu Newton pour expliquer le mouvement de la Lune autour de la Terre : la Lune tombe « continuellement » vers la Terre, formant ainsi une orbite stable. Ce phénomène permet également d’expliquer la situation de la Terre autour du Soleil, en assimilant les planètes et satellites en un point concentrant toute la masse du solide. Ce mouvement, inscrit dans un champ de gravitation, est indépendant de sa masse.
Le Soleil a également un mouvement par rapport aux planètes du système solaire, que l’on peut définir grâce à l’inertie. Pour rappel, le principe d’inertie est le suivant : « Dans un référentiel galiléen, si la somme des forces extérieures appliquées à un système mécanique est nulle, alors son centre d’inertie G est au repos ou possède un mouvement rectiligne uniforme. ». Plus l’inertie d’un corps est grande, plus il sera difficile d’arrêter son mouvement. L’inertie étant proportionnelle à la masse d’un corps, la Terre et toutes les autres planètes vont donc avoir un mouvement beaucoup plus rapide que le Soleil, et donc plus « visible ». Le mouvement du Soleil est plus léger, et principalement dû aux planètes plus lourdes que la Terre comme Jupiter.
Résumer avec l'IA :






















Si vous désirez une aide personnalisée, contactez dès maintenant l’un de nos professeurs !
Bonjour, suite à vos textes sur la gravitation,
Dans le cadre de la RG, la pomme lâchée s’accélère vers la terre. Si la gravitation n’est pas une force, la pomme devrait disposer d’un mouvement inertiel et non pas accéléré . Ou même rester immobile.
Ce n’est pas le cas. Comment l’expliquer?. Merci pour vos travaux.
Je ne comprends la valeur de la constante de Newton G = 6,67 x 10-11 N.m2.kg-2 transformée en G = 6,67408 x 10-11 m3.kg-1.s-2 . Comment explique-t-on ce changement d’ unité, merci d » avance .
Bonjour, avez-vous essayé de contacter l’un de nos professeurs pour recevoir une aide personnalisée ? Excellente journée ! :)
déterminer si la force de gravitation est proportionnelle,inversement proportionnelle oui dépendante des masse de deux systèmes A et B
Merci beaucoup je connais beaucoup plus maintenant que lorsque je n’avais pas lu l’article
Merci infiniment
Bonjour
Comment peut on montrer que l’intensité de la force d’attraction universelle exercée par le soleil sur la Lune varie entre deux valeurs extrêmales F Max et F Min que l’on déterminera.
est ce qu’en augmentant la masse de Mars on augmenterait sa gravité ? si oui cela changerait-il sa position orbitale ?
Comment on calcule la masse , si on a toutes les autres à partir de la formule ?