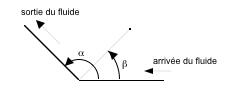
 | Soit un dièdre d’angle α à l’intérieur duquel s’écoule un fluide parfait incompressible. Cet écoulement sera supposé irrotationnel et permanent. |
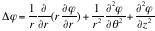
On suppose que le potentiel des vitesses peut être mis sous la forme φ(r,θ) = f(r).g(θ)
Les parois étant de grande hauteur, on poura raisonner dans un plan z = cte.
1 - Etablir une équation différentielle satisfaite par φ. Déduire celle satisfaite par f et g.
Mettre cette équation sous la forme :
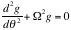
2 - Quelles sont a priori toutes les formes possibles pour g(θ) ?
3 - Chercher f sous la forme f(r) = C.r n et et donner l’expression de n en fonction de α.
4 - En déduire le champ des vitesses à l’intérieur du dièdre. Montrer que le module de la vitesse est indépendant de θ.
5 - Déterminer l’équation des lignes de courant. Tracer l’allure de ces lignes pour α = 3π/2.
Tracer l’allure des trajectoires des particules.
6 - Comment évolue le module de la vitesse d’une particule de fluide le long d’une ligne de courant pour α < π , et α > π ? Vers quelle valeur tend ce module au voisinage de l’arête ?
Résumer avec l'IA :













Si vous désirez une aide personnalisée, contactez dès maintenant l’un de nos professeurs !