Chapitres
- 01. Rappel
- 02. Les priorités
- 03. La distributivité
Savoir calculer, c'est bien sûr indispensable. Savoir rendre la monnaie, partager avec ses amis, ou encore compter son argent de poche ou faire ses comptes, les calculs sont partout.
Dans la vie de tous les jours, il nous arrive souvent de réaliser des calculs simples. Que ce soit à l'école, pour faire ses courses ou gérer son argent de poche ; il est donc essentiel de connaître les différentes règles de calcul.
Pour apprendre à les faire, regardons comment s’effectuent les opérations qui les constituent.
Rappel
Une opération est un processus utilisant un opérateur et qui vise à obtenir un résultat.
Il existe quatre opérations élémentaires :
- L'addition ;
- La soustraction ;
- La multiplication ;
- La division.
Le résultat d'une addition est appelé une somme et l'opérateur est le signe "+". Les nombres que l'on additionne sont appelés les termes. L'addition est commutative : 
Le résultat d'une soustraction est appelé une différence et l'opérateur est le signe "-". Attention, la soustraction n'est pas commutative :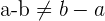 
Le résultat d'une multiplication est appelé un produit et l'opérateur est le signe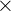 
, ou en langage informatique "*". Les nombres qui sont multipliés s'appellent les facteurs. La multiplication est commutative :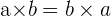 
Le résultat d'une division est appelé le quotient ou le rapport et l'opérateur utilisé est le signe ÷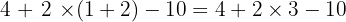
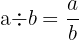Attention, la division n'est pas commutative :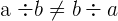 
Un calcul est un ensemble d'opérations. Dans un calcul, c'est la dernière opération que l'on effectue qui donne son nom à l'ensemble du calcul.
Les priorités
Maintenant que nous connaissons les quatre opérations élémentaires, passons aux priorités qui s'appliquent lorsque l'on effectue des calculs regroupant différentes opérations.
Les calculs sans parenthèses
Commençons par étudier les calculs sans parenthèses. Lorsque le calcul contient uniquement des additions et des soustractions, on effectue les opérations de la gauche vers la droite. Il en est de même lorsque le calcul contient uniquement des multiplications et des divisions.
Par exemple:
4-3+1=1+1=2
Si le calcul possède seulement des additions ou uniquement des multiplications, on peut effectuer les opérations dans n'importe quel ordre. Cela n'a pas d'importance.
Par exemple,
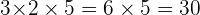mais c'est aussi égal à 3 fois 10 qui vaut 30.
De même pour l'addition :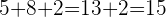 
mais c'est aussi égal à 5+10 qui vaut aussi 15.
Ensuite, dans un calcul toujours sans parenthèses, les multiplications et les divisions sont prioritaires sur les additions et les soustractions. Attention, cette règle est l'une des plus importantes.
Par exemple,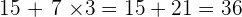 
ou encore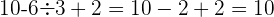 
Les calculs avec parenthèses
Enfin, regardons les calculs qui contiennent des parenthèses. Dans ce cas, on commence par effectuer les opérations se trouvant à l'intérieur des parenthèses. À l'intérieur d'une parenthèse, on applique les règles vues précédemment. Il en est de même lorsqu'il n'y a plus de parenthèses.
Regardons des exemples :
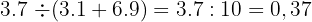
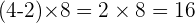
Imaginons des exemples un peu plus compliqués :
On commence toujours par les calculs dans la parenthèse : 4+2x5.
On doit commencer par effectuer la multiplication :
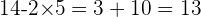
Une fois toutes les parenthèses calculées, on a:
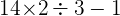
Les multiplications et divisions sont prioritaires, comme plusieurs d'entre elles se suivent, on les effectue de la gauche vers la droite :
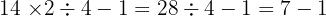
Finalement, il ne reste qu'une soustraction :
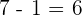
Regardons un autre calcul :
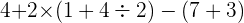
On commence par calculer les parenthèses :
Dans la première parenthèse
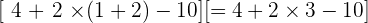
Maintenant, on effectue la multiplication:
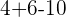
Enfin, on effectue les calculs de la gauche vers la droite :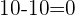 
Récapitulons nos règles de calcul avec ce tableau détaillant des exemples avec les règles qu'ils permettent d'appliquer.
| Règle de calcul | Résultat | |
|---|---|---|
| 15-3x4 | La multiplication est prioritaire sur la soustraction | 15-12=3 |
| 10/2x3 | Les opérations s'effectuent de gauche à droite | 5x3=15 |
| (5+3)/4 | La parenthèse est prioritaire | 8\4=2 |
| 4-(3-1) | La parenthèse est prioritaire | 4-2=2 |
Tableau récapitulatif des priorités de calcul
| Ordre | Opération | Exemple |
|---|---|---|
| 1 | Parenthèses | (3 + 5) × 2 |
| 2 | Puissances / Racines | 4² ou √16 |
| 3 | Multiplications / Divisions | 6 × 3 ou 20 ÷ 5 |
| 4 | Additions / Soustractions | 7 + 2 ou 10 − 4 |
La distributivité
Qu'est-ce que la distributivité ?
En mathématiques, on dit que la multiplication est distributive sur l'addition et la soustraction.
Énonçons mathématiquement cette propriété :
Soient a, b et c trois nombres.
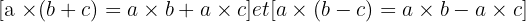
Lorsque l'on transforme
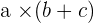en
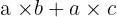
on dit que l'on a développé l'expression. Lorsque l'on effectue la transformation dans l'autre sens, on dit que l'on a factorisé. Ainsi:
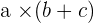
est la forme factorisée (sous forme de produit) et
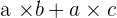est la forme développée (sous forme de somme).
Regardons divers exemples :
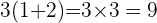
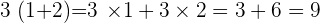
Dans ce genre de calculs, la distributivité n'est pas très utile, mais lorsque l'on a une inconnue, notée x, on trouve tout l'intérêt. Par exemple:
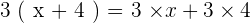
Regardons d'autres exemples de distributivité :
| Calculs | Résultat pour X=2 | |
|---|---|---|
| 2(X-1) | 2X-2 | 2 |
| 4(3-X) | 12-4X | 4 |
| X(4-2) | 2X | 4 |
| 5(1-X+2) | 5(-X+3)=-5X+3 | -10+3=-7 |
En mathématiques, il existe l'opération puissance qui consiste à multiplier un nombre par lui même plusieurs fois. Si l'on multiplie un nombre "a" par lui même n fois, on dira que l'exposant est n.
On notera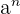 
L'opération contraire est la racine n-ième, notée 
Au collège, on étudie la puissance de 2, aussi appelée le carré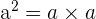 
L'opération inverse étant la racine carrée :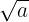 
Les exposants (et donc le carré) sont prioritaires sur les multiplications, divisions, additions et soustractions.
Par exemple,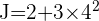 
On réalise en premier lieu les puissances.
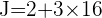
On passe ensuite aux multiplications et divisions :
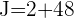
On termine par les additions et soustractions.
Bien-sûr, les parenthèses sont toujours prioritaires, même devant les exposants.
On a par exemple,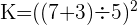 
On commence par la parenthèse intérieure, puis la suivante jusqu'à éliminer toutes les parenthèses.
Finalement, on obtient 
Vous avez aimé cet article ? Notez-le !
Loading...
Si vous désirez une aide personnalisée, contactez dès maintenant l’un de nos professeurs !
J’aimerais qu’on me résolve
(2/3+1/6)/(2-1/2)*3
Merci
Bonjour, avez-vous essayé de contacter l’un de nos professeurs pour recevoir une aide personnalisée ? Excellente journée ! :)
Pouvez-vous m’aider svp
Bonjour, comment pourrions-nous vous aider ?
c est tre bien explique
Merci pour votre soutien :)