Amélioration des performances, nouvelles technologies, révolutions techniques… Même le sport amateur n’y échappe pas. La thématique du sport et de la performance est traitée de différentes manières par les mathématiciens.
Pour améliorer votre passion pour un sport, ou pour les maths, ou encore pour les deux, lisez cet article sur le rôle des maths dans le sport !
Calculs géométriques en basket, golf ou ski
Les mathématiques sont essentielles au golf pour calculer la distance, l'angle et la trajectoire du swing.
Les joueurs utilisent des calculs géométriques pour évaluer les distances et ajuster les tirs en fonction de l'élévation du terrain.
La précision mathématique permet d'améliorer la stratégie de jeu en tenant compte des conditions météorologiques et des obstacles sur le parcours.
Le calcul d’une trajectoire parabolique au basket
La trajectoire d'un ballon de basket suit une courbe parabolique, représentée par une équation quadratique de la forme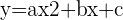 
.
Pour comprendre cette trajectoire, vous devez mesurer trois paramètres clés :
- L'angle de lancement
- La vitesse initiale
- La hauteur initiale du ballon
Supposons que vous lancez le ballon avec un angle de 45°, une vitesse initiale de 8 m/s, depuis une hauteur de 2 mètres. La position verticale 
en fonction de la distance horizontale 
est donnée par l'équation suivante :
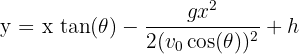
où 
est l'accélération due à la gravité, environ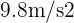 
.
Pour commencer, lancez le ballon et mesurez les paramètres de votre lancer
Par exemple, si vous mesurez un angle de 45° et une vitesse initiale de 8 m/s, vous pouvez insérer ces valeurs dans l'équation pour prédire la trajectoire :
- La formule devient :
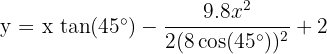
Ensuite, allez sur le terrain et faites quelques lancers. Enregistrez où le ballon atterrit et sa hauteur maximale
Par exemple, si un ballon lancé à 45° avec une vitesse de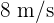 
atteint une hauteur maximale calculée de 4 mètres, vous pouvez comparer cette valeur avec vos observations.
En traçant la courbe théorique sur du papier millimétré ou en utilisant une application de traçage, vous pouvez visualiser la trajectoire prédite par les calculs et la comparer avec la trajectoire réelle. Cela vous permet d'ajuster vos mesures et vos paramètres pour améliorer la précision de vos lancers.
🏀 Mieux encore, cela vous aide à déterminer le potentiel de joueurs comme Wembanyama !
Les mathématiques vous aideront également à gérer votre argent.
Le théorème de Pythagore au golf
Le théorème de Pythagore est une règle mathématique qui permet de calculer la distance entre deux points dans un espace à deux dimensions, ce qui est très utile pour estimer les distances sur un parcours de golf.
La réciproque du théorème de Pythagore consiste à dire que si le carré de l'hypoténuse est égal à la somme des carrés des longueurs des deux autres côtés, alors le triangle est rectangle. Autrement dit, c’est une méthode pour vérifier que l’on a bien affaire à un triangle rectangle.
Cours Superprof
Le théorème de Pythagore s'énonce comme suit : dans un triangle rectangle, le carré de l'hypoténuse (le côté opposé à l'angle droit) est égal à la somme des carrés des deux autres côtés.
Formellement, si 
est l'hypoténuse et 
et 
sont les autres côtés, alors :
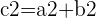
Imaginons que vous êtes sur le parcours de golf et que vous souhaitez calculer la distance entre votre balle et le trou. Vous savez que :
- La distance horizontale (d'une borne de parcours à une autre) est de 150 mètres
- La distance verticale (d'une position légèrement en hauteur) est de 40 mètres
- Pour trouver la distance directe , vous appliquez le théorème de Pythagore
En utilisant l'équation, vous avez :
Donc, la distance directe entre votre balle et le trou est d'environ 155,2 mètres
🏌️♂️ En plus de vous aider à déterminer la meilleure stratégie pour atteindre le trou souhaité, le théorème de Pythagore vous permet de choisir le bon club pour votre coup en tenant compte de la véritable distance.
Apprendre les mathématiques dès le plus jeune âge nous aidera à l’avenir. Saviez-vous?
Le calcul d’une descente au ski selon l’inclinaison
Comprendre la pente d'une piste de ski peut vous aider à évaluer sa difficulté et à ajuster votre technique en conséquence.
La pente d'une piste peut être calculée en utilisant la géométrie simple, en particulier en mesurant la dénivellation (différence de hauteur) et la distance horizontale parcourue
La pente 
est l'angle que forme la surface de la piste avec l'horizontale. On peut utiliser la tangente de cet angle pour le calculer, car dans un triangle rectangle, la tangente de l'angle est le rapport entre le côté opposé et le côté adjacent.
Imaginons que vous êtes sur une piste de ski et que vous voulez calculer la pente. Vous mesurez que sur une distance horizontale de 200 mètres , vous descendez de 50 mètres en hauteur. Pour trouver l'angle de la pente , vous utilisez la formule de la tangente :
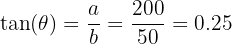
Pour trouver l'angle , vous utilisez l'inverse de la tangente (aussi appelé arctangente) :
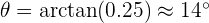
Donc, l'angle de la pente de votre piste est d'environ 14 degrés
⛷️Avec cette information, vous pouvez mieux évaluer la difficulté de la pente et ajuster votre technique de ski en conséquence. Cela vous permet également de choisir les pistes qui correspondent le mieux à votre niveau de compétence.
Les cours de maths sont très importants !
Statistiques dans le sport : football et baseball
Les mathématiques sont cruciales dans le football pour analyser les statistiques des joueurs, comme les passes réussies et les tirs au but.
Les équipes utilisent les probabilités pour prédire les résultats des actions de jeu et ajuster leurs stratégies.
Les calculs de trajectoire aident à prévoir les passes et les tirs précis, optimisant ainsi les performances individuelles et collectives sur le terrain.
Pourquoi peut-il être intéressant d’apprendre les mathématiques dès la maternelle ?
Les performances analysées via statistiques au foot
Les statistiques permettent de mesurer et d'évaluer divers aspects du jeu, fournissant des données précieuses pour les joueurs et les entraîneurs, comme le nombre de passes réussies, le nombre de tirs cadrés, les kilomètres parcourus.
Supposons que vous suiviez un milieu de terrain sur plusieurs matchs et que vous obteniez les données suivantes :
- Passes réussies : 85%
- Tirs cadrés : 40%
- Kilomètres parcourus par match : 10 km
- Interceptions par match : 5
Pour analyser ces données, vous pouvez utiliser des concepts statistiques simples. Disons que vous suivez les performances d'un joueur sur 5 matchs et que vous recueillez les données suivantes pour les passes réussies :
- Match 1 : 80%
- Match 2 : 90%
- Match 3 : 85%
- Match 4 : 88%
- Match 5 : 82%
Pour calculer la moyenne des passes réussies, vous additionnez les pourcentages et vous divisez par le nombre de matchs :
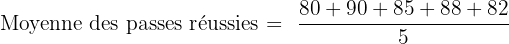
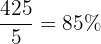
Vous pouvez également analyser d'autres aspects comme la variabilité des performances. Par exemple, pour évaluer la constance, vous pourriez calculer l'écart-type des passes réussies. Une faible variabilité indique une performance plus constante.
⚽️ Cette approche mathématique permet d'apporter des améliorations concrètes et mesurables aux performances, rendant l'analyse statistique essentielle pour le développement des compétences en football. Demandez à votre prof de vous apprendre ça en cours de maths !
Les probabilités de réussite au baseball
Les statistiques offrent des informations précieuses sur les performances des joueurs et des équipes, tandis que les probabilités aident à prédire les résultats des actions de jeu.
Imaginons que vous souhaitez analyser la performance d'un joueur au bâton. Vous pouvez recueillir des données sur plusieurs aspects, comme le nombre de coups sûrs, les fois où il arrive sur base (OBP, pour On-Base Percentage), le nombre de home runs, etc. Voici un exemple de données pour un joueur sur une saison :
- Coups sûrs : 150
- Apparitions au bâton : 500
- Home runs : 30
- Fois sur base : 200
Pour calculer la moyenne au bâton (BA, pour Batting Average) du joueur, vous divisez le nombre de coups sûrs par le nombre d'apparitions au bâton :
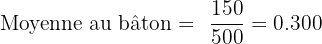
Pour calculer le pourcentage de présence sur base (OBP), vous divisez le nombre de fois où le joueur arrive sur base par le nombre total d'apparitions au bâton :
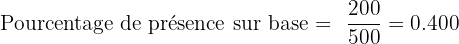
Vous pouvez également utiliser des probabilités pour prédire des actions spécifiques. Par exemple, si vous savez qu'un joueur a 30 home runs en 500 apparitions au bâton, la probabilité qu'il frappe un home run lors de sa prochaine apparition est :
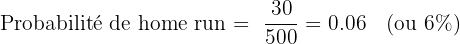
Les probabilités peuvent également aider à la prise de décisions en temps réel pendant un match. Par exemple, si les données montrent qu'un joueur est plus susceptible de frapper un certain type de lancer, le lanceur peut ajuster sa stratégie en conséquence.
Pourquoi peut-il être important d’apprendre les mathématiques ?
Calculs arithmétiques (vitesse) au tennis
Les mathématiques sont essentielles au tennis pour calculer la vitesse de la balle, l'angle de frappe et la distance parcourue.
Les joueurs utilisent des calculs trigonométriques pour ajuster leurs placements et leurs angles de tir.
L'analyse statistique des performances aide à évaluer les forces et les faiblesses, facilitant l'amélioration de la stratégie et de la précision des coups sur le court.
Quelle relation les mathématiques et l’argent peuvent-ils entretenir ? Découvrez-le ici.
La vitesse de la balle au tennis
Imaginons que vous souhaitez calculer la vitesse de votre coup de service au tennis. Vous avez enregistré que la balle a parcouru une distance de 20 mètres depuis votre raquette jusqu'à l'autre côté du court, et vous avez chronométré que cela a pris 1 seconde. Pour calculer la vitesse de la balle, vous utiliserez la formule :
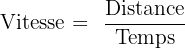
Appliquez la formule en utilisant la distance de 20 mètres et le temps de 1 seconde :
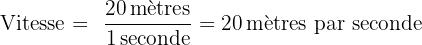
Pour améliorer votre service, vous pouvez également suivre vos vitesses de service sur plusieurs sessions d'entraînement. Voici comment vous pouvez procéder :
- Chronométrez la balle lors de plusieurs coups de service.
- Notez la distance parcourue par la balle pour chaque coup.
- Utilisez ces données pour calculer la vitesse de chaque coup et suivez votre progression au fil du temps.
Supposons que vous avez chronométré la distance parcourue par la balle pour trois revers différents :
- 1er coup de revers : 15 mètres en 0.75 secondes
- 2ème coup de revers : 14 mètres en 0.70 secondes
- 3ème coup de revers : 16 mètres en 0.80 secondes
Pour trouver la vitesse de chaque service :
🎾 En utilisant ces calculs, vous pouvez évaluer la constance de votre vitesse de service et identifier les domaines nécessitant des améliorations. Cela vous permet de travailler de manière ciblée pour développer une technique de service plus efficace et plus puissante, essentielle pour réussir sur le court de tennis. Vous ne verrez plus vos cour de math de la même manière !
Vous avez aimé cet article ? Notez-le !
Loading...
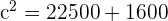
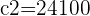
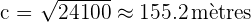
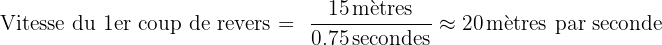
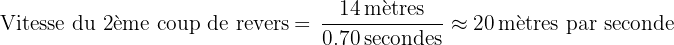
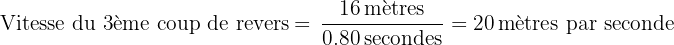
Bonjour, j’adore l’exotisme.
Moi aussu
moi aussi
super
Très intéressant vraiment