Chapitres

Notion d'immobilité
Immobilité d'un système ponctuel
Un système ponctuel est un système qui se réduit à un seul point. On dit d'un point qu'il est immobile s'il reste à la même place. On dit aussi de ce point qu'il est à l'équilibre. Cela implique alors que :
- ses coordonnées restent constantes au cours du temps (tout comme son vecteur position associé)
- sa vitesse (qui est une dérivée des coordonnées) reste nulle au cours du temps (tout comme son vecteur vitesse associé)
Immobilité d'un système non ponctuel
Un système non ponctuel est comme son nom l'indique, un système qui est constitué de plus d'un point. Cela peut par exemple être un objet solide. Un système non ponctuel est immobile si tous ses points sont immobiles. Remarque : il possible que certains points d'un corps soient immobiles alors que les autres sont en mouvement. Par exemple, les points de l'axe d'une boule en rotation sont immobiles alors que tous les autres sont en mouvement et ont une vitesse d'autant plus élevée qu'ils sont éloignés de l'axe. 
Lien entre référentiel et immobilité
La vitesse d'un système dépend du référentiel choisi, et par conséquent, son immobilité aussi. Si un système est immobile dans un référentiel noté R1 alors il l'est aussi dans tous les référentiels fixes par rapport à ce référentiel R1. Par contre, il est en mouvement dans tout autre référentiel qui serait mobile par rapport au référentiel R1. Prenons l'exemple d'un objet posé sur le sol d'une maison :
- Cet objet est immobile par rapport au référentiel de la maison
- Il est également immobile par rapport au référentiel terrestre (dans lequel la maison est immobile)
- Mais, il est en mouvement dans les référentiels géocentrique et héliocentrique où le référentiel terrestre est en mouvement. En effet, la Terre tourne sur elle même, l'objet est donc en mouvement par rapport au référentiel géocentrique. La Terre tourne également autour du soleil, l'objet est donc en mouvement par rapport au référentiel héliocentrique.

Conditions pour qu'un système ponctuel soit à l'équilibre
Quelles sont les conditions pour qu'un système ponctuel soit immobile ?
On dit d'un système ponctuel qu'il est en équilibre (ou immobile) si :
- il n'est soumis à aucune force. Ce cas théorique est en pratique irréalisable, puisqu'aucun objet n'est totalement isolé, ne serait-ce qu'à cause de sa masse qui implique une interaction gravitationnelle.
ou
- il est soumis à des forces qui se compensent.
Remarques :
- D'après le principe d'inertie, la réciproque n'est pas vraie : si un corps n'est soumis à aucune force ou à des forces qui se compensent alors il n'est pas obligatoirement au repos. En effet, il peut aussi posséder un mouvement rectiligne uniforme.
- Une conséquence des conditions décrites plus haut est qu'un système ponctuel soumis à une seule force ne peut nécessairement pas être immobile.
Exemple de l'équilibre d'un système ponctuel soumis à deux forces
Si un système ponctuel est soumis à deux forces, alors elles doivent se compenser pour que ce système soit à l'équilibre. Cela implique alors que :
- les deux forces doivent avoir la même direction, la même valeur mais des sens opposés.
- la somme des deux vecteurs force est nulle
- les deux vecteurs force sont opposés.
Le schéma ci-dessous reprend bien ces éléments :
- Sur le premier cas de figure, les deux forces ont bien la même direction, la même valeur et des sens opposés. La somme des deux vecteurs force est bien nulle. Pour finir, les deux vecteurs force sont orientés dans des sens opposés
- Sur les autres cas de figure, il y a toujours au moins une des conditions qui n'est pas réunie (les deux vecteurs force ont des directions différentes, les deux vecteurs forces sont dans le même sens, ou les forces n'ont pas la même valeur)
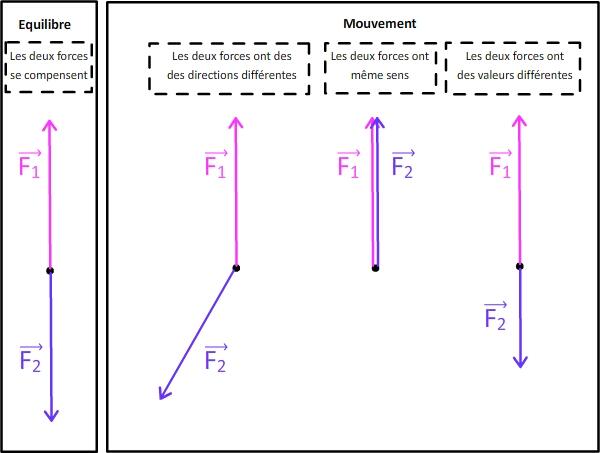
Quelques exemples de cas de figures possibles lorsqu'un système ponctuel est soumis à deux forces
Exemple de l'équilibre d'un système ponctuel soumis à trois forces ou plus
Si un système ponctuel est soumis à trois forces, les trois forces doivent se compenser pour que ce système soit à l'équilibre. Cela implique alors que la somme des trois vecteurs force (que l'on appellera F1, F2 et F3) est nulle. Si l'on définit un repère orthonormé associé au référentiel d'étude, alors il est possible d'obtenir des relations entre les coordonnées de ces trois vecteurs force : - xF1 + xF2 +xF3 = 0 - yF1 + yF2 +yF3 = 0 - zF1 + zF2 +zF3 = 0 Si ces trois relations sont respectées, alors on peut alors conclure à la possibilté d'un équilibre. Puis, dans le cas où l'équilibre est établi avec certitude, ces relations peuvent même permettent de déduire la valeur des forces correspondantes. Les deux schémas ci-dessous illustrent le cas où le système ponctuel est soumis à trois forces qui se compensent et se trouve donc dans un état d'équilibre. En effet, l'association des trois vecteurs force (schéma de droite) montre que la somme des trois vecteurs est nulle. 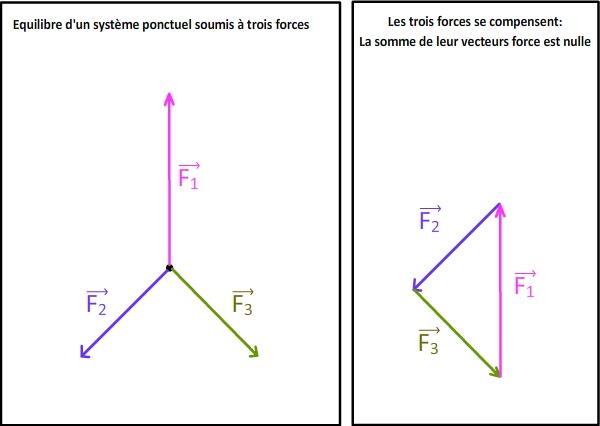
Conditions pour qu'un solide non ponctuel soit à l'équilibre
Dans le cas d'un solide, les conditions d'équilibre énoncées plus haut pour le système ponctuel ne sont pas suffisantes (même si la plupart du temps on s'y limite tout de même afin de simplifier l'étude de différentes situations). En effet, si un solide est soumis à des forces qui se compensent, celles-ci ne peuvent modifier la vitesse de translation mais par contre, elles peuvent provoquer un mouvement de rotation. Cette rotation n'est néanmoins pas possible si :
- le solide est soumis à deux forces ayant la même droite d'action
- les forces ont le même point d'application
Equilibres stables et équilibres instables
On distingue deux types d'équilibres :
- On dit qu'un système est dans un équilibre stable si, lorsqu'il est très légèrement écarté de sa position d'équilibre, les forces auxquelles il est soumis tendent à le ramener à cette position.
- A contrario, on dit qu'un système est dans un équilibre instable si, lorsqu'il est très légèrement écarté de sa position d'équilibre, les forces auxquelles il est soumis tendent à l'éloigner encore plus de cette position.

Résumer avec l'IA :























Si vous désirez une aide personnalisée, contactez dès maintenant l’un de nos professeurs !
Bonjour,
Pourriez-vous m’indiquer l’origine de la photo de la maison bleue en équilibre ?
Nous souhaiterions l’utiliser pour une couverture de livre.
Merci d’avance pour votre réponse.
Bien cordialement,
Pascaline Bressan
Editions Robert Laffont