Chapitres
Les puissances de 10 permettent d'exprimer des nombres très grands ou très petits de façon plus simple et plus compacte. Par exemple :
Le nombre de molécules dans une goutte d'eau est environ égal à 6 000 000 000 000 000 000 000 000
➡️
Au lieu d'écrire ce nombre en entier, on peut l'exprimer en utilisant les puissances de 10 : 6 x 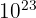 molécules
molécules
Cela rend l'écriture du nombre plus facile à lire et à écrire. De même, pour exprimer un nombre très petit comme la taille d'un atome, on peut utiliser les puissances de 10 :
? La taille d'un atome d'hydrogène est d'environ 0,000 000 000 1 mètre
➡️
Soit 1 x 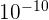 mètre en puissance de 10
mètre en puissance de 10

Écriture et signification d'une puissance de dix
Rédiger une puissance de dix
Un nombre correspondant à une puissance de dix s'écrit sous la forme 10a où "a" est un nombre entier relatif (c'est-à-dire un nombre entier qui peut être soit positif, soit négatif).
Ce nombre (10a) peut se lire de deux façons différentes :
"10 puissance a" ou "10 exposant a"
Quelques exemples de puissances de dix : 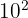 ;
; 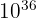 ;
; 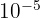
Signification d'une puissance de dix
Lorsque l'exposant (a) est positif, alors la puissance de dix 10a correspond au nombre 1 suivi d'un nombre de zéros correspondant au chiffre a. Quelques exemples :
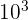 correspond au nombre 1 suivi de 3 zéros donc
correspond au nombre 1 suivi de 3 zéros donc 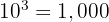
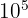 correspond au nombre 1 suivi de 5 zéros donc
correspond au nombre 1 suivi de 5 zéros donc 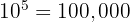
Lorsque l'exposant (a) est négatif, alors la puissance de dix 10a correspond à un nombre décimal s'écrivant avec le chiffre 1 dont le rang après la virgule correspond à la valeur de a. Quelques exemples :
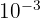 correspond au nombre 0,001 (le 1 est au 3ème rang après la virgule)
correspond au nombre 0,001 (le 1 est au 3ème rang après la virgule)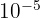 correspond au nombre 0,00001 (le 1 est au 5ème rang après la virgule)
correspond au nombre 0,00001 (le 1 est au 5ème rang après la virgule)
Comment écrire un nombre en puissance de dix

La méthode pour les nombres "simples"
Cette écriture n'est possible que pour des nombres qui ne sont composés que d'un seul chiffre "1" accompagné d'un ou plusieurs "0".
Pour un nombre entier (plus grand que 1), on doit compter le nombre de zéros qui suivent le chiffre "1". Ce nombre de zéros est noté "b". On peut alors écrire le nombre sous la forme 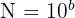 .
.
✅ Exemple : pour le nombre 10 000, on a quatre chiffres zéro, donc b = 4, et on peut écrire 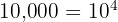 .
.
Si le nombre est un décimal inférieur à 1, on doit compter le rang du chiffre "1" après la virgule. On note ce nombre "b" et on écrit le nombre sous la forme 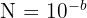 .
.
✅ Exemple, pour le nombre 0,0001, le 1 est au quatrième rang après la virgule, donc b = 4, et on peut écrire 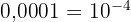 .
.
Pour un nombre > 1 (ex: 1000) : L'exposant est positif et égal au nombre de zéros après le 1. (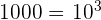 ).
).
Pour un nombre < 1 (ex: 0,01) : L'exposant est négatif et égal au rang du 1 après la virgule. (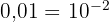 ).
).
Valeur des premières puissances de dix : Tableau
Le puissance de 10 tableau ci-dessous reprend l'écriture des puissances de dix allant de 10 puissance -10 à 10 puissance 10 :
| 10 puissance 10 | 10 puissance 9 | 10 puissance 8 | 10 puissance 7 | 10 puissance 6 | 10 puissance 5 | 10 puissance 4 | 10 puissance 3 | 10 puissance 2 | 10 puissance 1 | 10 puissance 0 | 10 puissance -1 | 10 puissance -2 | 10 puissance -3 | 10 puissance -4 | 10 puissance -5 | 10 puissance -6 | 10 puissance -7 | 10 puissance -8 | 10 puissance -9 | 10 puissance -10 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1010 = 10 000 000 000 | 109 = 1 000 000 000 | 108 = 100 000 000 | 107 = 10 000 000 | 106 = 1 000 000 | 105 = 100 000 | 104 = 10 000 | 103 = 1 000 | 102 = 100 | 101 = 10 | 100 = 1 | 10-1 = 0,1 | 10-2 = 0,01 | 10-3 = 0,001 | 10-4 = 0,0001 | 10-5 = 0,00001 | 10-6 = 0,000001 | 10-7 = 0,0000001 | 10-8 = 0,00000001 | 10-9 = 0,000000001 | 10-10 = 0,0000000001 |
Remarques :
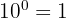 (par convention)
(par convention)- L'utilisation des puissances de dix devient clearly intéressante dès que les valeurs manipulées sont très grandes ou très petites.
Les préfixes : Tableau de conversion des puissances de dix
Les préfixes qui permettent de définir les multiples et sous-multiples d'une unité de base (comme le mètre, le gramme, etc.) sont tous associés à des puissances de dix. Ce tableau de conversion puissance de 10 est essentiel en sciences.
Le tableau ci-dessous reprend les préfixes les plus connus et les puissances de dix qui leur sont associées :
| 1021 | 1018 | 1015 | 1012 | 109 | 106 | 103 | 102 | 101 | 10-1 | 10-2 | 10-3 | 10-6 | 10-9 | 10-12 | 10-15 | 10-18 | 10-21 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Z (zetta) | E (exa) | P (peta) | T (tera) | G (giga) | M (méga) | k (kilo) | h (hecto) | da (déca) | d (déci) | c (centi) | m (milli) | µ (micro) | n (nano) | p (pico) | f (femto) | a (atto) | z (zepto) |
Des préfixes ont été ajoutées aux unités de base du Système International afin de pouvoir plus facilement manier de grands nombres. On parlera d'un kilo (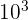 ). Pour le méga, puissance de 10 équivalente à
). Pour le méga, puissance de 10 équivalente à 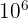 , et le giga, puissance de 10 à
, et le giga, puissance de 10 à 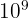 , ils sont courants en informatique. À l'inverse, le micro, puissance de 10 valant
, ils sont courants en informatique. À l'inverse, le micro, puissance de 10 valant 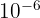 , est fréquent en biologie.
, est fréquent en biologie.
Il existe
aux unités de grandeur
Voici la liste des principaux préfixes, des plus petits aux plus grands :
Les sous-multiples (petits nombres)
- Yocto (y) :
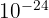
- Zepto (z) :
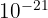
- Atto (a) :
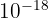
- Femto (f) :
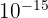
- Pico (p) :
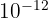
- Nano (n) :
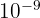 (nanomètre)
(nanomètre) - Micro (µ) :
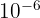 (micromètre, micro puissance de 10)
(micromètre, micro puissance de 10) - Milli (m) :
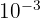 (milligramme)
(milligramme) - Centi (c) :
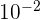 (centimètre)
(centimètre) - Déci (d) :
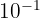 (décilitre)
(décilitre)
L'unité et les multiples (grands nombres)
- Unité :
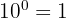 (mètre, gramme, etc.)
(mètre, gramme, etc.) - Déca (da) :
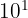
- Hecto (h) :
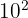
- Kilo (k) :
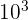 (kilogramme)
(kilogramme) - Méga (M) :
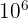 (mégaoctet, mega puissance de 10)
(mégaoctet, mega puissance de 10) - Giga (G) :
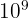 (gigawatt, giga puissance de 10)
(gigawatt, giga puissance de 10) - Téra (T) :
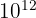 (téraoctet)
(téraoctet) - Péta (P) :
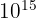
- Exa (E) :
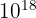
- Zetta (Z) :
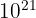
- Yotta (Y) :
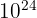
Règles et méthode de calcul de puissance de 10
Produits, quotients et exposants
Maîtriser le calcul de puissance de 10 est essentiel. Voici les règles fondamentales à connaître (où 'a' et 'b' sont des entiers relatifs) :
- Produit (multiplication) : On additionne les exposants.
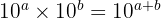
Exemple : 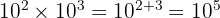
- Quotient (division) : On soustrait les exposants.
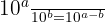
Exemple : 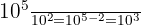
- Puissance d'une puissance : On multiplie les exposants.
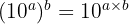
Exemple : 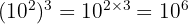
- Inverse : Un exposant négatif correspond à l'inverse.
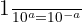
Exemple 1 : 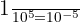
Exemple 2 : 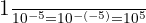
Si vous souhaitez en savoir plus sur les méthodes de calcul, vous pouvez approfondir le sujet en consultant cet article !
Applications : écriture scientifique et ordre de grandeur
Écriture scientifique des valeurs
L'écriture scientifique (ou notation scientifique) est une technique utilisée pour représenter n'importe quel nombre décimal. L'écriture scientifique est de la forme 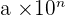 .
.
 est un nombre décimal tel que
est un nombre décimal tel que 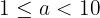 (il ne doit y avoir qu'un seul chiffre avant la virgule, et il ne doit pas être 0). C'est la mantisse.
(il ne doit y avoir qu'un seul chiffre avant la virgule, et il ne doit pas être 0). C'est la mantisse. (ou
(ou  dans nos exemples précédents) est un entier relatif (positif ou négatif). C'est l'exposant.
dans nos exemples précédents) est un entier relatif (positif ou négatif). C'est l'exposant.
Le nombre 0 ne peut pas être représenté avec la notation scientifique.
La notation scientifique peut aussi aider aux opérations car on peut facilement multiplier les mantisses entre elles et additionner les exposants (en utilisant les règles de calcul vues ci-dessus). Une autre notation peut aussi se retrouver, notamment dans les calculatrices scientifiques ou sur les ordinateurs. La lettre 'e' comme "exposant" remplace le 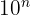 . Par exemple
. Par exemple 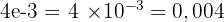 .
.
L'écriture scientifique est un sujet complexe qui peut être approfondi ici !
L'un des grands intérêts des puissances de dix est de simplifier l'écriture de très grandes ou très petites valeurs. Elles apportent un gain de temps considérable et limitent le risque d'erreur.

Estimation d'un ordre de grandeur
L'ordre de grandeur est une puissance de 10 qui sert à estimer un nombre, à donner une approximation simple. Il représente la puissance de 10 la plus proche du nombre exact. L'utilisation des ordres de grandeur facilite aussi les comparaisons entre différents éléments (planètes, atomes...) et permet de vérifier la cohérence d'un résultat de calcul.
L'ordre de grandeur de la distance Terre-Lune (384 000 km) est de 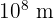 .
.
L'ordre de grandeur d'une molécule d'eau (0,4 nm) est de 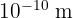 .
.
Pour déterminer l'ordre de grandeur, on reprend l'écriture scientifique : 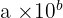
- Si
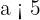 (strictement), alors l'ordre de grandeur de
(strictement), alors l'ordre de grandeur de 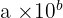 est
est 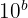
- Si
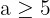 (supérieur ou égal), alors l'ordre de grandeur de
(supérieur ou égal), alors l'ordre de grandeur de 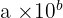 est
est 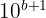
Écrire le nombre en notation scientifique : 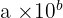 .
.
Regarder la mantisse (le nombre  ) :
) :
Si 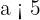 , l'ordre de grandeur est la puissance de dix du nombre :
, l'ordre de grandeur est la puissance de dix du nombre : 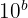 .
.
Si 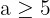 , l'ordre de grandeur est la puissance de dix supérieure :
, l'ordre de grandeur est la puissance de dix supérieure : 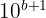 .
.
☀️ Prenons l'exemple du rayon du soleil : 695 700 km
695 700 km = 6,957 *105 km = 6,957*108 m
L'ordre de grandeur pour le rayon du soleil sera 109 m
Exercice d'application (puissance de 10)
Pour vous entraîner, voici un exercice puissance de 10 simple. Essayez de convertir les nombres suivants en notation scientifique, puis de donner leur ordre de grandeur.
3 450 000 000 (distance Terre-Soleil en km approx.)
Notation scientifique : 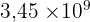 . Ordre de grandeur :
. Ordre de grandeur : 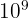 (car 3,45 < 5).
(car 3,45 < 5).
0,000 072 (taille d'un petit grain de pollen en m)
Notation scientifique : 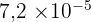 . Ordre de grandeur :
. Ordre de grandeur : 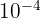 (car 7,2 ≥ 5, donc on fait 10^{-5+1}).
(car 7,2 ≥ 5, donc on fait 10^{-5+1}).
695 700 (rayon du soleil en km, vu plus haut)
Notation scientifique : 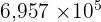 . Ordre de grandeur :
. Ordre de grandeur : 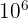 (car 6,957 ≥ 5, donc on fait 10^{5+1}).
(car 6,957 ≥ 5, donc on fait 10^{5+1}).
Simplifiez les expressions suivantes et donnez le résultat sous la forme d'une seule puissance de 10 :
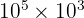
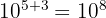 (Règle du produit)
(Règle du produit)
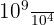
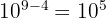 (Règle du quotient)
(Règle du quotient)
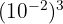
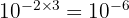 (Règle de la puissance)
(Règle de la puissance)
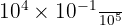
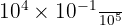
Donnez l'écriture scientifique des nombres suivants :
8 450 000
8 450 000 = 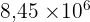
0,000231
0,000231 = 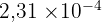
45 (Astuce : où est la virgule ?)
45 = 45,0 = 
La vitesse de la lumière : 299 792 458 m/s
299 792 458 = 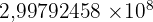 m/s
m/s
En vous aidant des préfixes, convertissez les valeurs suivantes dans l'unité de base (ex: Mètres, Octets, Grammes...).
Capacité d'une clé USB : 32 Giga-octets (Go) en octets. (Giga puissance de 10 = ?)
32 Go = 32 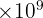 octets =
octets = 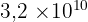 octets
octets
Taille d'une bactérie : 2 Micromètres (µm) en mètres. (Micro puissance de 10 = ?)
2 µm = 2  mètres
mètres
Puissance d'une centrale : 1,5 Mégawatts (MW) en watts. (Mega puissance de 10 = ?)
1,5 MW = 1,5 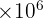 watts
watts
Poids d'un médicament : 500 milligrammes (mg) en grammes.
500 mg = 500 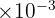 g = 0,5 g =
g = 0,5 g = 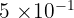 g
g

Et vous, que connaissez-vous des puissances de 10 ?
Résumer avec l'IA :























Si vous désirez une aide personnalisée, contactez dès maintenant l’un de nos professeurs !
Bonjour. On me demande de trouver le rapport entre 10puissance-10 et 10 puissance-15. Diamètre d’un atome et diamètre de son noyau.Je fais comment ? Merci 🙏
Bonjour, je cherche à résoudre cette question : Quel est la dernière égalité ?
19 + 16 = 17
13 + 13 = 8
12 + 12 = 6
11 + 9 = 11
Alors 10 + 10 = ?
Merci pour votre aide
Bonjour, je vous propose de découvrir nos formateurs sur Superprof, qui peuvent vous offrir une assistance sur mesure. Excellente journée à vous ! :)
________________________
6 000 000 000 000 000 000 000 000
➡️
Au lieu d’écrire ce nombre en entier, on peut l’exprimer en utilisant les puissances de 10 : 6 x 10^23 molécules
________________________
Bonjour
je révise avec ma fille.
Cette puissance ne devrait-elle pas être 6X10^24 ?
Merci de m’éclairer.
Très bonne journée
.cd
Y a un erreur kilo c’est 10 puissance 3 et pas 10 puissance deux
excellents articles. très utiles pour être à l’aise face aux élèves.
6 000 000 000 000 000 000 000 000 molécules correspondent à 6 x 10^24 molécules (non pas 6 x 10^23 molécules) n’est ce pas ?
C’est intéressant
Mehdislm30 2010