Chapitres
- 01. Généralités à propos du vecteur force
- 02. Mesurer une force : le Dynamomètre
- 03. Les lois de Newton : le cœur de la mécanique
- 04. Vecteurs associés aux forces les plus connues
- 05. Opérations sur les vecteurs forces : La somme vectorielle
- 06. Travail d’une force : L'énergie en mouvement
- 07. Composantes et Norme : Passer du dessin au calcul
- 08. Application avancée : Le plan incliné
- 09. Vecteur force : exercices pratiques et solutions
- 10. Sources
La physique est la science qui décrit comment l'univers se comporte, du mouvement des planètes à la chute d'une pomme. Au cœur de cette description se trouve un concept fondamental : l'interaction. Mais comment modéliser mathématiquement une poussée, une traction ou une attraction invisible ? La réponse tient en deux mots : vecteur force.
Le vecteur force est bien plus qu'une simple flèche dessinée sur un papier. C'est un outil puissant qui permet de prédire l'avenir d'un système mécanique. Il intègre des informations cruciales : direction, sens, intensité et point d’application. Comprendre le vecteur force est la clé de voûte pour aborder la mécanique newtonienne, l'ingénierie, et même la biomécanique.
Dans ce dossier complet, nous allons décortiquer ce concept sous tous ses angles, des définitions de base aux calculs complexes de décomposition vectorielle sur un plan incliné.
Définition : Outil mathématique représentant une action mécanique.
Notation : F (avec une flèche au-dessus).
4 caractéristiques : Point d'application, Direction (droite), Sens (flèche), Norme (valeur en Newtons).
Relation clé : Le vecteur poids (P) est l'exemple le plus courant.
Généralités à propos du vecteur force
Avant de plonger dans les formules, il est impératif de comprendre ce que représente physiquement ce vecteur. Une erreur courante est de confondre la force avec l'énergie ou la puissance. La force est une interaction instantanée.
Un peu d'histoire : d'Aristote à Newton
La notion de force n'a pas toujours été claire. Pendant l'Antiquité, Aristote pensait qu'il fallait une force constante pour maintenir un objet en mouvement. Il se trompait. C'est Isaac Newton, au XVIIe siècle, qui a révolutionné notre compréhension en liant la force non pas à la vitesse, mais à l'accélération (le changement de vitesse). Le vecteur force est né de la nécessité de quantifier cette relation de cause à effet.
Les effets de la force : Dynamique et Statique
Une force se manifeste par ses effets observables. On distingue deux grandes catégories d'effets :
L'effet dynamique : La force modifie l'état de mouvement d'un objet. Cela peut signifier :
- Mettre en mouvement un objet immobile (le départ d'un sprint).
- Arrêter un objet (le freinage d'une voiture).
- Changer la direction (un coup de raquette au tennis).
L'effet statique : La force déforme l'objet.
- Déformation élastique (temporaire) : tirer sur un ressort.
- Déformation plastique (définitive) : écraser une canette en aluminium.
Qu’est-ce qu’un vecteur force ?
Pourquoi utiliser des vecteurs ? Imaginez que vous deviez pousser une voiture en panne. Si trois personnes poussent avec une force de 500 N chacune, mais dans trois directions différentes, la voiture n'avancera pas efficacement. La valeur de la force ne suffit pas ; l'orientation est tout aussi cruciale. Le vecteur est l'outil mathématique parfait pour encapsuler ces données.
Le vecteur force est une application concrète d'un outil mathématique fondamental. Si la notion de direction, de sens et de norme vous semble encore floue, je vous conseille de lire d'abord notre guide complet sur les vecteurs et leur fonctionnement.
Caractéristiques du vecteur force
Pour définir un vecteur force sans ambiguïté, quatre caractéristiques doivent être précisées :
| Caractéristique | Détails techniques |
|---|---|
| Point d'application | C'est l'origine du vecteur. Pour une force de contact, c'est le point de contact. Pour une force à distance (gravité), c'est le centre de gravité G. |
| Direction | C'est la droite d'action. Elle peut être horizontale, verticale ou oblique avec un angle précis. Attention à ne pas confondre direction (la ligne) et sens. |
| Sens | Sur la ligne de direction, il y a deux possibilités. Le sens est indiqué par la pointe de la flèche (vers le haut, vers la droite, etc.). |
| Norme | C'est l'intensité de la force, sa "puissance". Elle se note | vec(F) | et s'exprime en Newtons (N). |
Notation du vecteur force
La rigueur est de mise en physique :
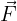désigne le vecteur (avec ses propriétés géométriques).
désigne la valeur numérique (un scalaire positif).
Exemple : On écrira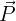 
pour le vecteur poids, mais 
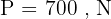pour dire "je pèse 700 Newtons".
Exemple d’une force : le cas du poids
L'exemple le plus concret est le vecteur poids (noté P). C'est la force d'attraction que la Terre exerce sur nous. Ses caractéristiques sont immuables :
- Point d'application : Le centre de gravité de l'objet (G).
- Direction : Toujours verticale.
- Sens : Toujours vers le bas (vers le centre de la Terre).
- Norme : Calculée via la formule
.
Mesurer une force : le Dynamomètre
Comment connaître la norme d'une force ? On utilise un instrument appelé dynamomètre. Il fonctionne généralement grâce à un ressort dont l'allongement est proportionnel à la force appliquée (Loi de Hooke).
La relation est :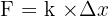 
Où 
est la raideur du ressort et 
son allongement. C'est ce principe qui est utilisé dans les pesons pour peser les bagages ou les poissons.
Les lois de Newton : le cœur de la mécanique
Le vecteur force prend tout son sens lorsqu'il est utilisé dans les trois lois fondamentales de Newton.
1ère Loi : Le Principe d'Inertie
Comment connaître la norme d'une force ? On utilise un instrument appelé dynamomètre. Il fonctionne généralement grâce à un ressort dont l'allongement est proportionnel à la force appliquée (Loi de Hooke).
La relation est :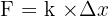
Où est la raideur du ressort et son allongement. C'est ce principe qui est utilisé dans les pesons pour peser les bagages ou les poissons.
2ème Loi : Le Principe Fondamental de la Dynamique
C'est la formule la plus célèbre de la mécanique :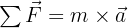 
Elle stipule que l'accélération 
d'un objet est proportionnelle à la force totale appliquée et inversement proportionnelle à sa masse. C'est ici que l'on comprend pourquoi il est plus dur de pousser un camion qu'un vélo !
3ème Loi : Le Principe d'Action-Réaction
Toute force résulte d'une interaction. Si un objet A pousse B, alors B pousse A avec la même intensité, mais en sens opposé : 
Vecteurs associés aux forces les plus connues
Un bon physicien doit savoir identifier les forces en présence pour faire un "bilan des forces".
Forces à distance
Elles agissent sans contact physique, à travers le vide.
Le vecteur Poids (P![]()
)
C'est la force de gravitation exercée par la Terre (ou un autre astre) sur un objet proche de sa surface. Attention, le poids est une force (en Newtons), la masse est une quantité de matière (en kg).
- Direction : Verticale du lieu.
- Sens : Vers le bas.
- Norme : (avec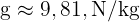
sur Terre).
Force électrique et magnétique
La force de Coulomb s'exerce entre des charges électriques. Deux charges de même signe se repoussent (vecteurs forces opposés s'éloignant), deux charges opposées s'attirent.
Forces de contact
La Réaction du support (R![]()
ou N![]()
)
Si vous posez un livre sur une table, il ne tombe pas. Pourquoi ? Parce que la table exerce une force de réaction perpendiculaire à sa surface vers le haut, qui compense exactement le poids.
La Tension (T![]()
)
C'est la force exercée par un fil, une corde ou un câble. La direction du vecteur est toujours celle du fil, et le sens va de l'objet vers le point d'attache.
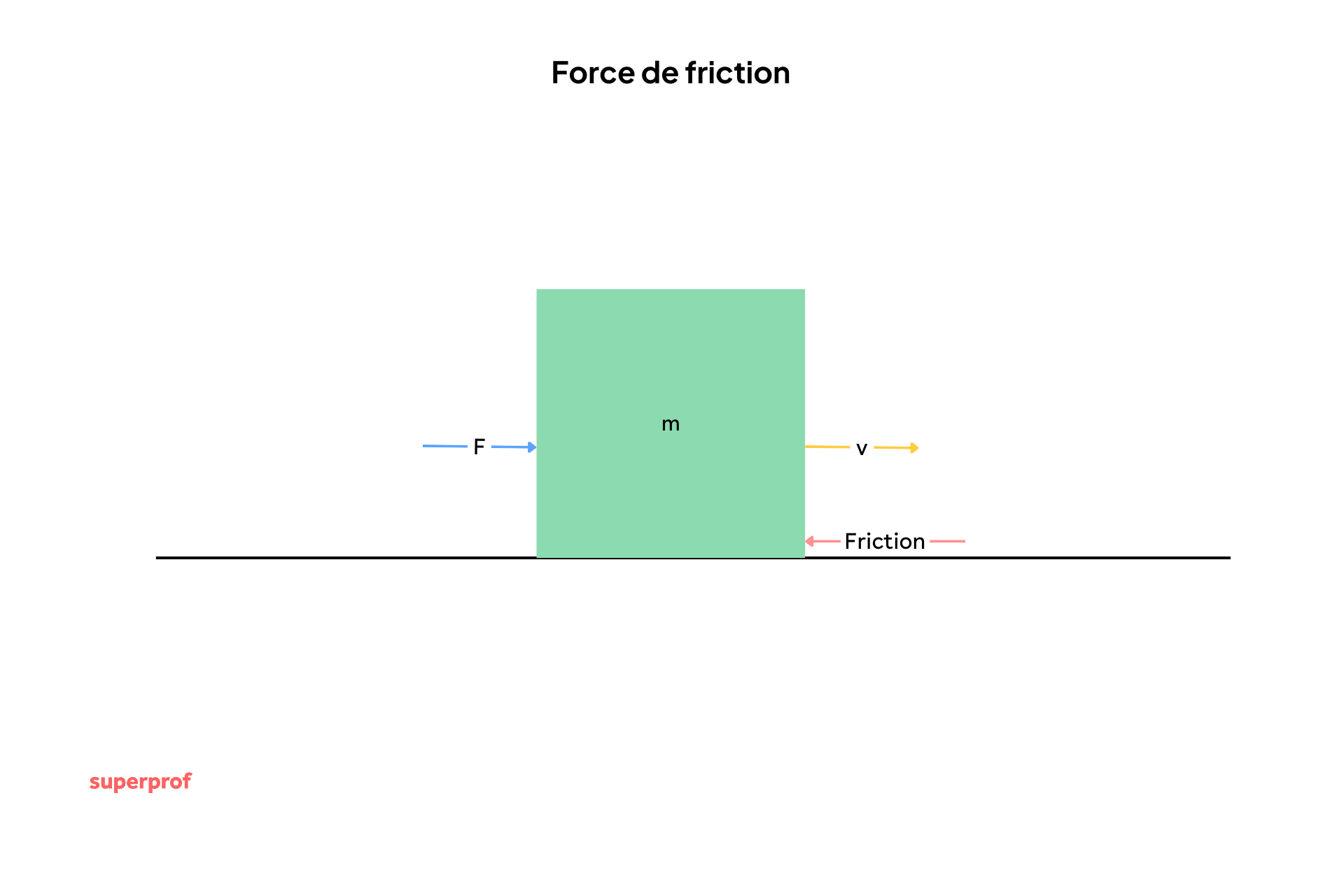
Les Frottements (f![]()
)
Aussi appelés forces de friction. C'est une force parallèle à la surface de contact mais de sens opposé au mouvement (ou à la tentative de mouvement). Sans frottements, nous ne pourrions pas marcher, nous glisserions sur place !
Poussée d’Archimède (Π![]()
)
« Tout corps plongé dans un fluide subit une poussée verticale, dirigée de bas en haut, égale au poids du volume de fluide déplacé. » C'est ce vecteur qui s'oppose au poids et permet la flottaison.
Opérations sur les vecteurs forces : La somme vectorielle
Souvent, plusieurs forces s'appliquent sur un même objet. Pour comprendre le mouvement résultant, il faut additionner ces vecteurs. Mais attention, on ne fait pas 2+2=4 !
La force résultante R est la somme vectorielle : La force résultante
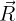est la somme vectorielle :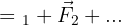 
Pour faire cette somme graphiquement, on utilise la règle du parallélogramme ou la méthode "bout à bout" (on place l'origine du deuxième vecteur à la pointe du premier).
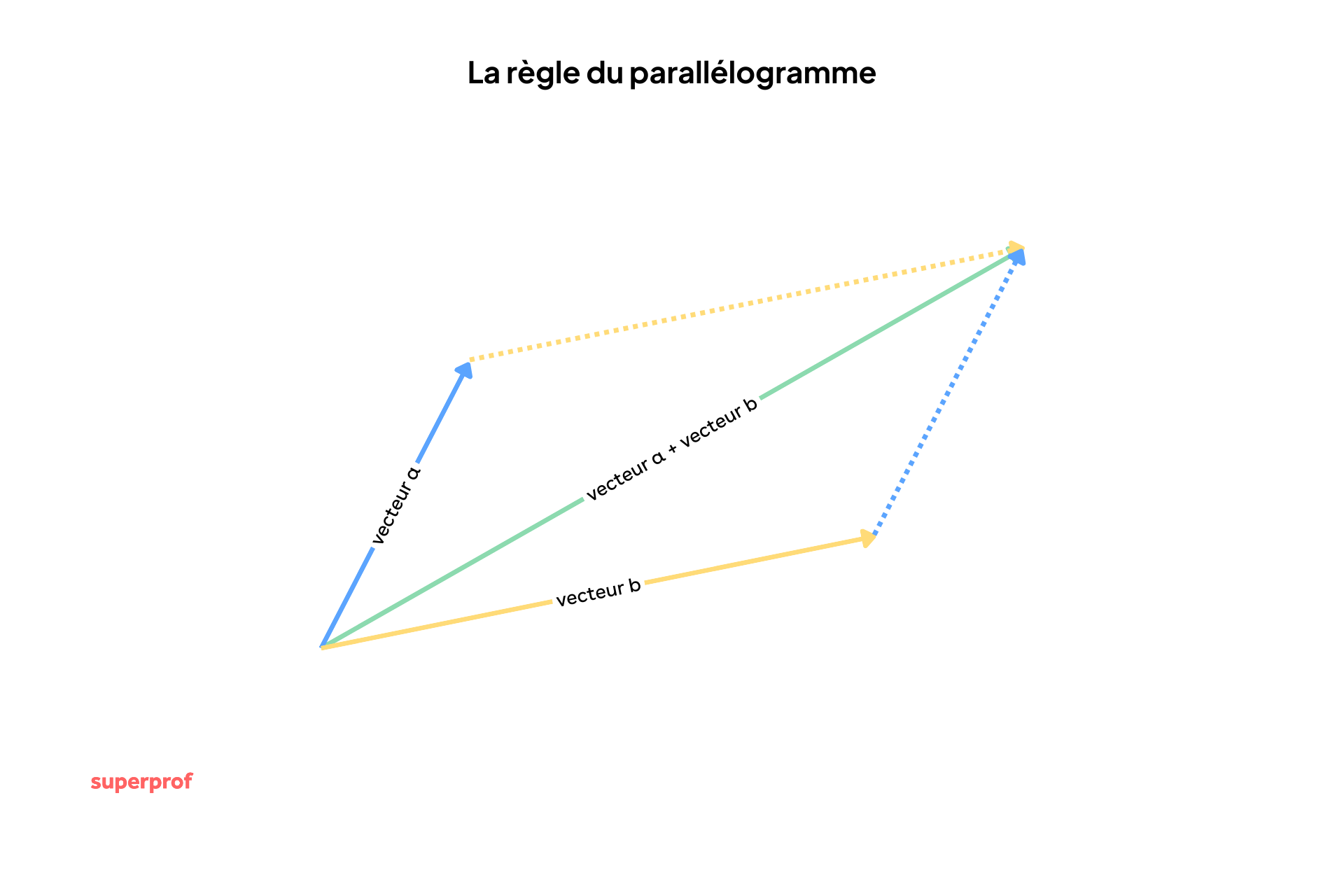
a et b.
Nous avons évoqué la construction graphique de la force résultante. Cette méthode repose sur une figure géométrique précise : pour savoir comment la tracer parfaitement, consultez notre fiche méthode sur vecteurs et parallélogramme.
Travail d’une force : L'énergie en mouvement
Définition
En physique, appliquer une force ne suffit pas à dire que l'on a "travaillé". Si vous poussez un mur de toutes vos forces pendant une heure mais que le mur ne bouge pas, le travail physique est nul (bien que vous soyez épuisé). Le travail nécessite un déplacement.
Formule du travail
Le travail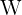 
(pour Work) s'exprime en Joules (J). Pour une force constante sur un trajet rectiligne 
:
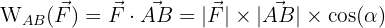
L'angle 
est crucial :
- Si
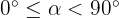(force dans le sens du mouvement) : Travail moteur (la force aide). - Si
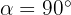(force perpendiculaire, ex: le poids sur une route plate) : Travail nul (la force ne consomme ni ne donne d'énergie au mouvement). - Si
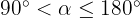(force opposée, ex: frottements) : Travail résistant (la force freine).
Composantes et Norme : Passer du dessin au calcul
Pour résoudre des problèmes complexes, le dessin ne suffit plus. Il faut projeter les vecteurs dans un repère orthonormé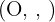 
.
Décomposition d'un vecteur force
Avant d'appliquer la racine carrée pour trouver l'intensité, il faut connaître les valeurs algébriques de la force. Si le passage du dessin aux chiffres vous pose problème, consultez notre fiche sur les coordonnées d'un vecteur.
Tout vecteur force 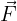peut être décomposé en deux vecteurs orthogonaux : 
.
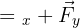Les composantes scalaires se calculent par trigonométrie :
Norme du vecteur force
Une fois que vous avez les composantes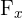 
et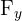 
, comment retrouver la valeur totale de la force ? On utilise le théorème de Pythagore.
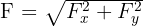
Si une force pousse de 30 N vers la droite (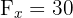
) et de 40 N vers le haut (
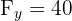), la force totale est : 
.
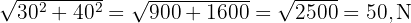Application avancée : Le plan incliné
C'est l'exercice classique qui terrifie les étudiants, mais qui illustre parfaitement l'utilité des vecteurs forces. Imaginez une caisse posée sur une rampe inclinée. Pourquoi glisse-t-elle ?
Le poids P est toujours vertical. Mais le mouvement se fait le long de la pente. Pour comprendre, il faut décomposer le vecteur poids en deux nouvelles forces fictives :
- La composante normale (Pn) : Perpendiculaire à la pente. Elle plaque la caisse contre la rampe. Elle est compensée par la réaction du support.
- La composante tangentielle (Pt) : Parallèle à la pente. C'est elle qui tire la caisse vers le bas et provoque la glissade !
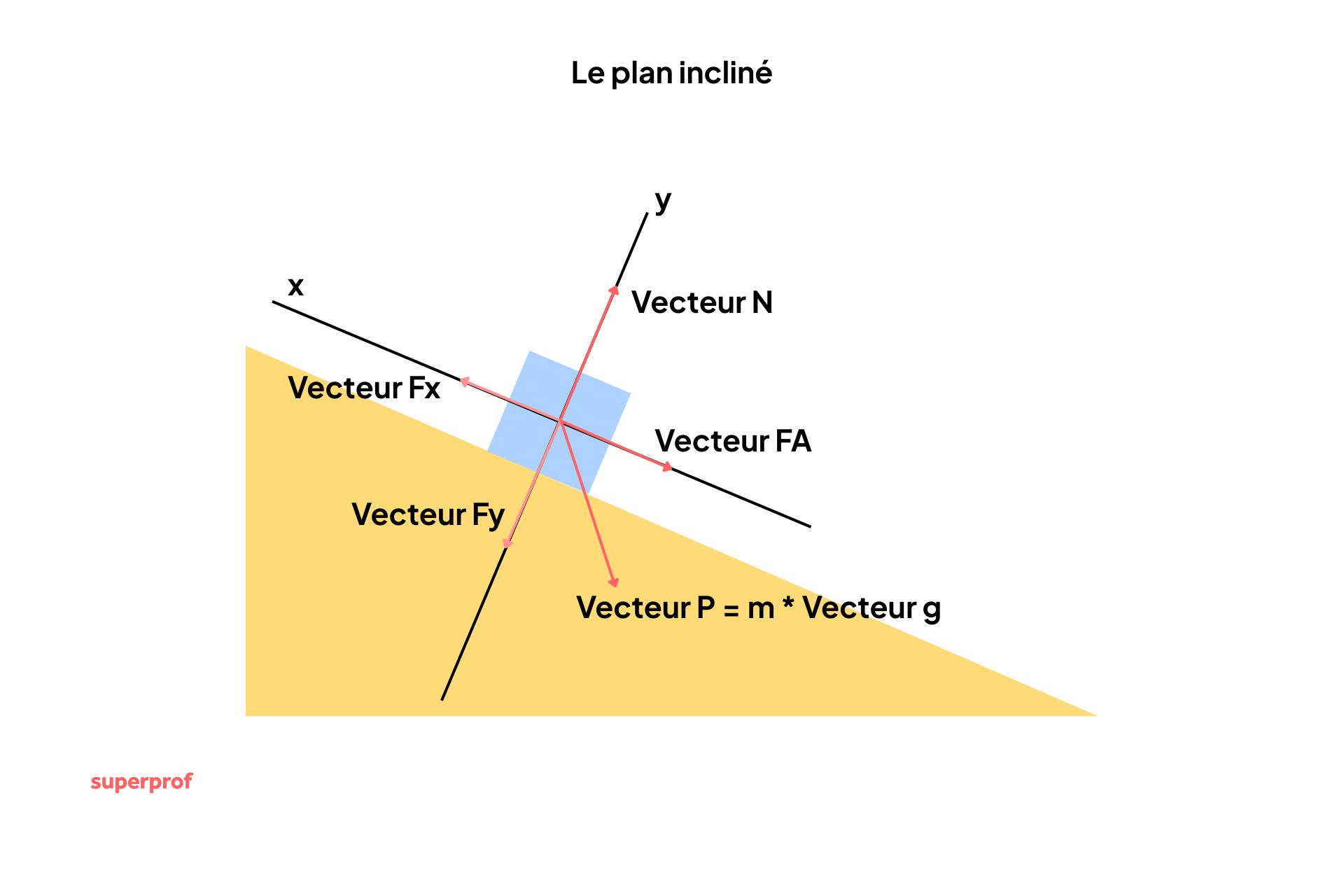
Sans la maîtrise de la décomposition vectorielle, impossible de calculer l'accélération de la caisse ou la force de frottement nécessaire pour qu'elle reste immobile.
Vecteur force : exercices pratiques et solutions
La théorie est acquise ? Passons à la pratique avec des cas concrets.
Exercice 1 : La valise à l'aéroport
Vous tirez une valise de 15 kg sur un sol plat. Vous exercez une force de traction de 50 Newtons, orientée vers le haut avec un angle de 60 degrés par rapport au sol.
Quelle est la force réelle qui fait avancer la valise horizontalement ? (Aide : le cosinus de 60° vaut 0,5).
Ce champ est requis.
Pour trouver la partie de la force qui agit réellement pour faire avancer la valise (et non pour la soulever), on multiplie la force totale par le cosinus de l'angle.
Calcul : 50 x 0,5 = 25 Newtons.
Conclusion : Seulement la moitié de votre effort sert à faire avancer la valise, le reste la soulève légèrement !
Quelle est la valeur du poids de la valise ? (Pour simplifier, on prendra la gravité g = 10 N/kg).
Ce champ est requis.
Le poids se calcule en multipliant la masse de l'objet par la gravité.
Calcul : 15 x 10 = 150 Newtons.
Exercice 2 : L'équilibre des forces
Un lustre de 5 kg est suspendu au plafond par un câble solide. Il est parfaitement immobile.
Quelle est la valeur de la Tension du câble (la force qui retient le lustre pour qu'il ne tombe pas) ? (On prendra ici la gravité précise g = 9,81 N/kg).
Ce champ est requis.
Le raisonnement Puisque le lustre est immobile, il est en équilibre. D'après le principe d'inertie, les forces s'annulent. Cela signifie que la force qui tire vers le haut (la Tension du câble) doit être exactement égale à la force qui tire vers le bas (le Poids du lustre).
Le calcul Calculons d'abord le poids du lustre : 5 kg x 9,81 = 49,05 Newtons.
Conclusion : Puisque la Tension est égale au Poids, la Tension du câble est donc de 49,05 Newtons, dirigée vers le haut.
Sources
- Benson, Harris. Physique 1 : Mécanique. De Boeck Supérieur, 2015. Consulté le 7 Février 2026.
- Commissariat à l'énergie atomique et aux énergies alternatives (CEA). "Les forces fondamentales." CEA.fr, 2021. Consulté le 7 Février 2026.
- Perez, José-Philippe. Mécanique : Fondements et applications. Dunod, 2014. Consulté le 7 Février 2026.
Résumer avec l'IA :
Vous avez aimé cet article ? Notez-le !
Loading...
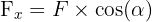
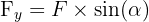
Si vous désirez une aide personnalisée, contactez dès maintenant l’un de nos professeurs !
Bonjour a quoi correspond :
-V eau déplacer (comment calculer)
– le k de k*|q1*q2|/r2
Celui qui traduit un effet statique de la force est?
Comment calculer un vecteur avec des variable inconnu telles que a,b,c
Exemple: OM = (2X-bY+5Z)i+(bX-3Y-7Z)j+(3X-4Y+cZ) . trouvez les variables a,b,c.
force électrostatique?
Celui qui traduit un effet statique de la force est? EX:A.un enfant qui lance un objet B.un basketteur qui envoir un ballon C.une branche d’arbre recourbée D.un débardeur qui soulève une charge