Chapitres

La radioactivité, principes et fonctionnement
Comme beaucoup d'autres découvertes scientifiques, le phénomène de radioactivité a été découvert complètement par hasard.
Le premier à l’avoir mis en évidence, c’est Henri Becquerel. Celui-ci faisait des recherches sur les liens potentiels entre les rayons X et la fluorescence. Pour cela, il utilisait une préparation de sel phosphorescent d’uranium.
Tout d’abord, il déposa ce sel sur des plaques photographiques enveloppées dans du papier noir.
Ensuite, il exposa cette préparation au soleil puis développa les plaques.
Les photographies montrent l’image des cristaux de sel d’uranium. Henri Becquerel en déduit que cette image a été créée par les rayons X découverts quelques temps plus tôt par Wilhelm Conrad Röntgen, un physicien allemand.
Le raisonnement de Becquerel est simple : il pense que l’énergie solaire est absorbée par l’uranium avant d’être réémise sous forme de rayons X.
Pour confirmer ses hypothèses, il souhaita poursuivre ses expériences. Mais ces expériences impliquaient la présence du Soleil qui se montra timide plusieurs jours durant.
Henri Becquerel a donc été contraint de repousser ses expérimentations et rangea ses plaques photographiques imprégnées de sel d’uranium dans un placard.
Quelques jours plus tard, il les ressortit et décida de les développer bien qu’il ne s’attende pas à trouver grand-chose.
En conclusion, la radioactivité a été découverte en 1896 par Henri Becquerel lors d'une étude concernant l'uranium et cette découverte sera confirmée plus tard par Marie Curie après une étude du radium.
Marie Skodowska-Curie est une physicienne et chimiste d’origine polonaise. Elle est très connue pour sa découverte de la radioactivité naturelle et des éléments 84 et 88 : le polonium et le radium. Elle reçut de multiples prix et distinctions pour ses recherches. Elle reçut en 1903 le prix Nobel de physique et en 1911 le prix Nobel de chimie. C’était la première femme à recevoir ce genre de distinction et encore à ce jour elle est la seule à en avoir reçu deux.
La radioactivité correspond à un phénomène physique au cours duquel des noyaux atomiques considérés comme instables, on les appelle alors radionucléides ou encore radioisotopes, se transforment, et ce de façon spontanée, en d'autres atomes tout en émettant par la même occasion des particules de matières comme des électrons, des noyaux d'hélium ou encore des neutrons et en émettant de l'énergie sous la forme de photons et d'énergie cinétique. On appelle cela une désintégration.
On appelle alors l'émission de particules, qu'elles soient matérielles ou immatérielles, rayonnement et on est capable de parler de rayonnements ionisants car l'énergie des particules est telle qu'elle est capable d'entraîner l’ionisation de la matière traversée. Il existe alors différents types de rayonnement que l'on listera un peu plus tard.
La radioactivité présente des effets sur les organismes subissant des rayonnements ionisants, on parle alors d'irradiation. Cependant, ces effets dépendent du niveau, mais aussi de la durée de l'exposition, qui peut être aiguë ou encore chronique, de la nature du rayonnement mais également de la localisation de la radioactivité. En effet, les effets ne seront pas les mêmes si l'exposition est interne que si l'exposition était externe ou encore en surface.
Les rayonnements provoqués par les substances radioactives sont très largement utilisés dans les différentes industries, notamment en ce qui concerne le contrôle de pièce manufacturées, les soudures, l'usure ou même à faible dose en médecine afin de déterminer un diagnostic ou dans une visée thérapeutique afin de soigner les cancers. Dans tous les cas, il est évident qu'il est nécessaire de suivre des mesures de prévention, de protection mais également de contrôle qui resteront adaptés au niveau de radioactivité observé.
Il existe trois types de radioactivité : la radioactivité bêta, la radioactivité alpha et la radioactivité gamma.
La radioactivité bêta
La radioactivité bêta est un type de désintégration radioactive où une particule bêta (électron ou positron) est émise. On parle de radioactivité bêta + quand un positron est émis mais on parle de radioactivité – quand c’est un électron qui est émis.
La radioactivité alpha
La radioactivité alpha est un rayonnement provoqué par une désintégration alpha qui est une désintégration radioactive où un noyau atomique éjecte une particule alpha qui se transforme en un autre noyau dont le nombre de masse est diminué de 4 et le numéro atomique de 2 à cause de la particule alpha manquante qui est analogue au noyau d’hélium 4.
La radioactivité gamma
La radioactivité gamma est un rayonnement provoqué par une désintégration gamma. Le plu souvent, ces désintégrations accompagnent des désintégrations alpha ou bêta. En effet, quand il émet un rayon alpha ou bêta, le noyau devient excité. Lors de l’émission d’un rayonnement électromagnétique gamma, le noyau peut donc redescendre à un état plus stable.
La décroissance radioactive
Quel que soit le radioisotope, il a autant de chance qu'un autre radioisotope de la même espèce de se désintégrer à un instant t. Il faut néanmoins savoir que la désintégration ne dépend pas des conditions physico-chimiques dans lesquels le nucléide étudié se trouve. En effet, on parle de la loi de désintégration radioactive comme étant une loi statique.
La loi s'énonce ainsi :
Soit N(t) le nombre de radionucléides d'une espèce donnée présents dans un échantillon à un instant t quelconque.
Puisque la probabilité de désintégration d’un radionucléide quelconque ne dépend ni du milieu qui l'entoure, ni de la présence d'autres espèces de radionucléide, le nombre total de désintégration, noté dN, pendant un intervalle de temps dt est proportionnel au nombre N de radionucléide de la même espèce présents mais aussi proportionnel à la durée dt de l'intervalle de réaction.
On obtient alors la formule : 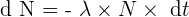
On peut observer le signe - puisque le nombre N de radionucléides diminue au cours du temps.
Si on intègre l'expression obtenue précédemment, on trouve alors la loi de décroissance exponentielle du nombre N(t). Ainsi, si on note N0 le nombre de radionucléides présents à l'instant t = 0, on obtient l'expression suivante :

Si on note t1/2 la demi-vie de l'élément étudié, il est possible d'obtenir l'expression suivante :
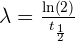
La notion d'activité est étroitement liée avec la décroissance radioactive. En effet, l'activité d'une source correspond à l'expression du nombre de désintégrations par secondes d'un atome composé d'un certain nombre de noyaux radioactifs. Cette grandeur s'exprime habituellement en becquerels de symbole Bq. On peut donc en déduire un taux de désintégration des noyaux atomiques.
Cependant, l'utilisation de cette unité pose parfois des problèmes. En effet, le becquerel est une unité petite. Par exemple, un élément radioactif dont la durée de demi-vie est d'un million d'années, une mole de cet élément aura une activité de 20 x 109 Bq.
Pour un échantillon de noyaux radioactifs, le temps de demi-vie est la durée au bout de laquelle la moitié des noyaux présents à un instant t se soit désintégrée.
Pour rappel, il faut des millions de Becquerels pour que cela devienne dangereux pour l'Homme.
Dans le cas où les radioisotopes sont dans un mélange, plus la demi-vie de celui-ci est courte et plus son activité massique sera forte.
La datation radioactive
On appelle datation radiométrique, ou encore radiochronologique, toute méthode de datation absolue utilisant la variation régulière au cours du temps de la proportion de radioisotopes dans certains corps. Très utilisées par les géologues, la plus connue reste la datation au carbone 14 mais aussi la technique Rubidium/Strontium.
Elle permet de dater les objets anciens en mesurant leur activité. Si on connaît l'activité d'une source à un instant présent, si on connait l'activité initiale on peut en déduire la durée écoulée depuis l'instant initial.
Exercices type BAC
Exercice 1 : La radioactivité au service de l'archéologie
Isotope radioactif du carbone, le "carbone 14" noté 14C est formé continuellement dans la haute atmosphère. Il est très réactif et donne rapidement du "gaz carbonique" (dioxyde de carbone) qui, en quelques mois, se mélange avec l'ensemble du gaz carbonique de notre atmosphère. Il sera donc assimilé par les plantes au même titre que le gaz carbonique produit avec du carbone stable (les isotopes 12C et 13C ). On le retrouvera donc comme constituant de la matière organique des animaux herbivores et carnivores. [...]
Vers 1950, le chimiste américain W. Libby a démontré [...] que tous les êtres vivants sont caractérisés par le même rapport du nombre de noyaux de 14C au nombre de noyaux de 12C : 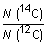
En conséquence, un gramme de carbone pur extrait d'un être vivant présente une activité due au 14C, voisine de 13,6 désintégrations par minute, ce qui correspond à "un âge zéro". Dans un animal ou un végétal mort (tronc d'arbre, coquille fossile, os... trouvé dans une caverne), le 14C "assimilé" par l'animal ou la plante quand il était vivant, décroît exponentiellement en fonction du temps du fait de sa radioactivité à partir de l'instant de sa mort. La comparaison(1) de cette activité résiduelle aux 13,6 désintégrations par minute fournit directement l'âge de l'échantillon fossile [...]. Au bout de 40 millénaires, iI reste moins de 1% du 14C que contenait initialement un échantillon fossile ; cette teneur résiduelle devient trop faible pour être déterminée avec précision.
J.C Duplessy et C. Laj
D'après une publication du CEA
Clefs CEA n°14 automne 1989
(1) : On suppose que la valeur 13,6 désintégrations par minute, pour un organisme vivant, est restée constante au cours des derniers
millénaires.

1. Désintégration du "carbone 14"
On donne les numéros atomiques suivants : Z = 6 pour le carbone (C) et Z = 7 pour l'azote (N).
1.1. Pourquoi les noyaux de symboles 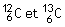
1.2. Donner la composition du noyau de symbole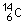
1.3. Le "carbone 14" se désintègre "en azote 14".
Ecrire l'équation de désintégration du "carbone 14" en supposant que le noyau fils n'est pas obtenu dans un état excité. S'agit-il d'une
radioactivité α, β+, β- ?
2. Propriétés des désintégrations radioactives
2.1. Donner les caractéristiques des transformations radioactives en complétant les phrases du cadre ci-dessous à l'aide des mots ou expressions proposés.
| 2.1.1 | La transformation radioactive d'un noyau possède un caractère... | |||
| Mots proposés : | ● prévisible | ● aléatoire | ● périodique | |
| 2.1.2. | La désintégration d'un noyau... celle d'un noyau voisin | |||
| Expressions proposées | ● n'affecte pas | ● modifie | ● est perturbée par | |
| 2.1.3. | Un noyau "âgé" a... de se désintégrer qu'un noyau "jeune". | |||
| Expressions proposées : | ● plus de chances | ● moins de chances | ● autant de chances | |
| 2.1.4. | L'évolution d'une population d'un grand nombre de noyaux radioactifs possède un caractère... | |||
| Mots proposés : | ● prévisible | ● aléatoire | ● périodique | |
2.2. On propose trois expressions mathématiques pour représenter l'évolution du nombre N de noyaux de "carbone 14" restant dans l'échantillon à la date t, λ étant la constante radioactive relative à la désintégration étudiée (λ > 0) :
(a) N = N0.e-λt
(b) N = N0— λt
(c) N = N0.e λt
2.2.1. Dans chacune des trois expressions ci-dessus :
● Que vaut N à t = 0 ?
● Quelle est la limite de N quand t tend vers l'infini ?
En déduire l'expression à retenir parmi les propositions (a), (b) et (c), en justifiant.
2.2.2. L'activité 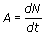
2.2.3. En s'aidant du texte, donner pour un échantillon de 1,0 g de carbone pur, extrait d'un être vivant, la valeur de A0.
2.2.4. A quel événement correspond "l'âge zéro" cité dans le texte ?
3. Datation au "carbone 14"
Le temps de demi-vie de l'isotope 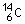
3.1. Qu'appelle-t-on temps de demi-vie t1/2 d'un échantillon radioactif ?
3.2. Montrer que λ.t1/2=ln2 à partir des réponses données aux questions 2, 2.1. et 3.1.
3.3. Calculer la valeur de λ dans le cas du "carbone 14", en gardant t1/2 en années.
3.4. Plusieurs articles scientifiques parus en 2004 relatent les informations apportées par la découverte d'Otzi, un homme
naturellement momifié par la glace et découvert, par des randonneurs, en septembre 1991 dans les Alpes italiennes.
Pour dater le corps momifié, on a mesuré l'activité d'un échantillon de la momie. On a trouvé une activité égale à 7,16 désintégrations par minute pour une masse équivalente à 1,0 g de carbone pur. Donner l'expression littérale de la durée écoulée entre la mort d'Otzi et la mesure de l'activité de l'échantillon. Calculer cette durée.
3.5. A Obock (en République de Djibouti), des chercheurs ont étudié un corail vieux de 1,2 × 105 ans (soit cent vingt mille ans).
D'après le texte, ce corail a-t-il pu être daté par la méthode utilisant le "carbone 14" ? Justifier la réponse.
4. Choix du radioélément
4.1. Pour dater des roches très anciennes, on utilise parfois la méthode potassium-argon.
Le "potassium 40", de demi-vie 1,3 × 109 ans, se transforme en "argon 40".
Quel pourcentage de noyaux de "potassium 40" reste-t-il dans une roche au bout de 4 fois le temps de demi-vie ?
4.2. Comme il est indiqué dans le texte pour le carbone 14", on suppose que la teneur résiduelle minimale permettant
d'effectuer une datation avec le "potassium 40" est également de 1 % de la teneur initiale.
En comparant l'âge de la Terre, qui est de 4.5 × 109 ans, à la demi-vie du "potassium 40", préciser si la méthode de datation par le "potassium 40" permet de mesurer l'âge de la Terre. Justifier la réponse.
Exercice 2 : La datation des séismes, l'exemple de la Californie
La radioactivité se manifeste dans tout l’Univers. On peut utiliser les éléments radioactifs comme des horloges. Selon leur nature et leur durée de vie, ils peuvent renseigner sur l’âge de l’Univers, l’âge de la Terre, les processus géologiques et même l’histoire de l’humanité. On se propose ici de déterminer les dates de tremblements de terre qui se sont produits au cours des siècles à proximité de la faille de San Andreas en Californie.

1. Radioactivité naturelle du carbone
1.1. Donner la composition en protons et en neutrons des noyaux atomiques suivants 126C et 146C.
1.2. Les deux noyaux du 1.1. sont dits isotopes. Justifier cette affirmation en définissant le mot isotopes.
1.3. Le carbone 14C est un noyau radioactif émetteur β–.
Écrire l’équation de la réaction nucléaire correspondante en la justifiant. On admet que le noyau fils
n’est pas obtenu dans un état excité.
1.4. Calculer l’énergie de liaison, en joules, du carbone 14C que l’on notera Eι (14C).
1.5. En déduire l’énergie de liaison par nucléon du carbone 14C (en joules par nucléon).
1.6. Calculer l’énergie libérée par la réaction de la question 1.3. (en joules).
Données :
- Numéros atomiques : Z(Be) = 4 , Z(B) = 5 , Z(C) = 6 , Z(N) = 7 , Z(O) = 8 ;
- Célérité de la lumière dans le vide : c = 2,998 x 10 8 m.s –1.
- Masses de quelques particules :
| Particule | Proton | Neutron | Electron | Noyau 14C | Noyau 14N |
|---|---|---|---|---|---|
| Masse (kg) | 1,672621 x 10-27 | 1,674927 x 10-31 | 9,109381 x 10-31 | 2,32584 x 10-26 | 2,32527 x 10-26 |
2. Datation par le carbone 14C
Deux scientifiques, Anderson et Libby, ont eu l’idée d’utiliser la radioactivité naturelle du carbone 14C pour la datation. Les êtres vivants, végétaux ou animaux, assimilent du carbone. La proportion du nombre de noyaux de 14C par rapport au nombre de noyaux de 12C reste constante pendant toute leur vie. À la mort de l’organisme, tout échange avec le milieu naturel cesse et les atomes de 14C disparaissent peu à peu. La radioactivité décroît alors avec le temps selon une loi exponentielle, qui permet d’atteindre un ordre de grandeur de l’âge de l’échantillon analysé. On admet que le rapport entre le nombre de 14C et 12C est resté constant dans les êtres vivants au cours des derniers millénaires.
2.1. On note N(t) le nombre de noyaux radioactifs d’atomes de « carbone 14 » à un instant de date t pour un échantillon et N0 le nombre de noyaux radioactifs à un instant pris comme origine des dates (t0 = 0 s) pour ce même échantillon. On note λ la constante radioactive.
Écrire la loi de décroissance radioactive.
2.2. Temps de demi-vie et constante radioactive.
2.2.1. Donner la définition du temps de demi-vie d’un échantillon radioactif que l’on notera t1/2.
2.2.2. Retrouver l’expression littérale du temps de demi-vie en fonction de la constante radioactive :
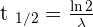
2.2.3. Le temps de demi-vie de l’isotope du carbone 14C est 5,70 x 10 3 ans.
En déduire la valeur de la constante radioactive λ en an-1.
2.3. L’activité A(t) d’un échantillon radioactif à l’instant de date t est donnée ici par l’expression :
A(t) = λ . N(t)
2.3.1. Définir l’activité et donner son unité dans le système international.
2.3.2. En utilisant cette expression et la loi de décroissance, déduire que :

où A0 est l'activité à l'instant de date t0 = 0 s.
3. La faille de San Andreas
En 1989, à proximité de la faille de San Andreas en Californie, on a prélevé des échantillons de même masse de végétaux identiques ensevelis lors d’anciens séismes. On a mesuré l’activité de chacun
d’eux. On admet que cette activité est due uniquement à la présence de 14C.
| Numéro de l'échantillon | 1 | 2 | 3 |
|---|---|---|---|
| Activités de l’échantillon (SI) | 0,233 | 0,215 | 0,223 |
3.1. L’activité d’un échantillon de même végétal vivant et de même masse est A0 = 0,255 SI. On note t la durée qui s’est écoulée entre l’instant de date t0 = 0 s du séisme et l’instant de la mesure.
Déterminer la valeur t3 qui correspond à l’échantillon n°3.
3.2. En déduire l’année au cours de laquelle a eu lieu le séisme qui correspond à l’échantillon n°3 étudié en 1989.
3.3. Pour les échantillons 1 et 2, on propose les années 586 et 1247. Attribuer à chaque échantillon, l’année qui correspond. Justifier sans calcul.
Exercice 3 : Déterminer l'âge de la Terre
La détermination de l'âge de la Terre a commencé vers le XVIe siècle, on l'estimait alors autour
de 5 000 ans. Au XIXe siècle, des scientifiques admettaient un âge d'environ 100 millions d'années.
La découverte de la radioactivité, par H. Becquerel en 1896, bouleversa toutes les données connues.
La datation à l'uranium - plomb permit de déterminer assez précisément l'âge de la Terre.
Nous proposons de comprendre cette technique de datation.
1. Étude de la famille uranium 238 – plomb 206
Le noyau d'uranium 238, naturellement radioactif, se transforme en un noyau de plomb 206, stable, par une série de désintégrations successives. Nous allons étudier ce processus.
(On ne tiendra pas compte de l'émission g ).
1.1. Dans la première étape, un noyau d'uranium 238 92 U subit une radioactivité α. Le noyau fils est du thorium (symbole Th).
1.1.1. Qu'est-ce qu'un noyau radioactif ?
1.1.2. Écrire l'équation de la réaction nucléaire en précisant les règles utilisées.
1.2. Dans la deuxième étape, le noyau de thorium 234 se transforme en un noyau de protactinium
2. Géochronologie
On a constaté d'une part, que les minéraux d'une même couche géologique, donc du même âge, contiennent de l'uranium 238 et du plomb 206 en proportions remarquablement constantes, et d'autre part que la quantité de plomb dans un minéral augmente proportionnellement à son âge relatif.
Si on mesure la quantité de plomb 206 dans un échantillon de roche ancienne, en considérant qu'il n'y en avait pas initialement, on peut déterminer l'âge du minéral à partir de la courbe de décroissance radioactive du nombre de noyaux d'uranium 238.
Étudions un échantillon de roche ancienne dont l'âge, noté tTerre, correspond à celui de la Terre.
2.1. On considère la courbe de décroissance radioactive du nombre NU(t) de noyaux d'uranium 238 dans un échantillon de roche ancienne.
2.1.1. Indiquer la quantité initiale NU(0) de noyaux d'uranium.
2.1.2. Déterminer graphiquement la valeur de la constante de temps t de l'uranium 238. En déduire la valeur de sa constante de radioactivité l.
2.1.3. Donner l'expression de NU(t), nombre de noyaux radioactifs présents dans l'échantillon à la date t, en fonction de NU(0).
Calculer le nombre de noyaux d'uranium 238 qui restent dans la roche à la date t1 =1,5.109 années.
2.1.4. Définir et déterminer graphiquement le temps de demi-vie tl/2 de l'uranium 238.
2.2. La quantité de plomb mesurée dans la roche à la date tTerre, notée Npb(tTerre), est égale à 2,5.1012 atomes.
2.2.1. Établir la relation entre NU (tTerre), NU(0) et Npb(tTerre). Calculer la quantité NU (tTerre)de noyaux d'uranium.
2.2.2. Déterminer l'âge tTerre de la Terre.
Résumer avec l'IA :























Si vous désirez une aide personnalisée, contactez dès maintenant l’un de nos professeurs !
Corrigé !