Chapitres
Tout objet en mouvement (déformable ou non) est un mobile. Dans le cas d’un solide par exemple, l’étude de quelques points permet de connaître parfaitement le mouvement d’un mobile.
? D’ailleurs, le mobile lui-même (qu’il soit déformable ou non) peut être considéré comme un point mobile si on ne s’intéresse qu’à son mouvement global.
Quelques exemples :
- Sur un trajet en voiture de Aix en Provence à Marseille, une voiture peut être considérée comme un point mobile
- Mars, vue du Soleil peut être considérée comme un point mobile car son rayon est petit par rapport à sa distance au Soleil
Découvrez tout ce qu'il faut savoir sur le mouvement, la trajectoire et la vitesse ?

La notion de trajectoire ⚽️

Pour étudier le mouvement d’un système on a toujours besoin de se fixer un référentiel : c’est un objet par rapport auquel on étudiera le mouvement de notre système.
En simplifiant, on peut définir le référentiel comme quelque chose correspondant au milieu au sein duquel on étudie le mouvement.
Définition : La trajectoire d’un point matériel est l’ensemble des positions successives occupées par ce point au cours du temps. Elle dépend du référentiel choisi.
? En effet, si on choisi de prendre l'exemple du voyageur assit dans un train en marche alors le référentiel va changer selon l'observateur :
- Par rapport à un observateur sur le quai, le voyageur est en mouvement
- Par rapport à un observateur dans le train, le voyageur est immobile.
Ainsi, il est possible de conclure que, pour décrire le mouvement d’un mobile, il faut choisir un repère d’espace ou référentiel.
Une trajectoire d’un point correspond à l’ensemble des positions occupées par ce dernier au cours de son mouvement. C’est une courbe. On distingue plusieurs types de trajectoire parmi lesquels les plus simples sont:
- La trajectoire rectiligne : ce qui correspond au fait que le mobile se déplace sur une droite. Le mouvement est d’ailleurs appelé mouvement rectiligne.
- La trajectoire circulaire qui correspond au fait que le mobile se déplace sur un arc de cercle. Le mouvement est appelé mouvement circulaire.
- Lorsque la trajectoire correspond à une courbe qui n’est pas un cercle on parle de trajectoire curviligne. Le mobile se déplace sur une courbe quelconque, plane ou non. Le mouvement est appelé curviligne.
? Il existe aussi des trajectoires qui s’effectuent selon des figures géométriques plus complexes (comme par exemple les trajectoires hélicoïdales ou elliptiques).
Deux types de mouvement sont très importants dans l’étude des systèmes :
La translation
La rotation
- La translation : Dans un mouvement de translation, chaque segment de droite, appartenant au mobile, reste parallèle à lui-même, au cours du déplacement et tous les points du mobile ont des trajectoires identiques de même longueur.
- La rotation : Dans un mouvement de rotation, tous les points du mobile décrivent des cercles ou des arcs de cercles centrés sur une droite fixe que l'on appelle axe de rotation. On peut notamment illustrer ce mouvement avec l'exemple des aiguilles d’une horloge.
- Si la trajectoire est une droite, la translation est rectiligne, comme dans le cas d'un ascenseur.
- Si la trajectoire est une courbe, la translation est curviligne, comme dans le cas d'un téléphérique.
- Si la trajectoire est un cercle ou un arc de cercle, la translation est circulaire, comme dans le cas d'une grande roue.
Définition : Une translation correspond à une droite passant par 2 points quelconques du solide qui reste parallèle au cours du mouvement
Définition : Une rotation correspond à un mouvement où tous les points décrivent des cercles dont les centres sont alignés et tous les plans sont parallèles.
La notion de référentiel ?
La description d’un mouvement nécessite toujours le choix préalable d’un objet indéformable servant de centre de référence : ce solide est appelé solide de référence ou référentiel. Le mouvement étudié est donc relatif au référentiel choisi.
? On appelle référentiel galiléen tout référentiel au sein duquel le principe d'inertie est vérifié
Même s'il n'existe aucun référentiel galiléen au sens strict. Il est cependant possible de considérer certains référentiels usuels comme galiléen si certaines conditions sont vérifiées :
Le référentiel terrestre
Le référentiel géocentrique
Le référentiel héliocentrique
Référentiels galiléens
? On déduit du principe d'inertie qu'il n'est pas nécessaire qu'il y ait une force pour qu'il y ait un mouvement. Les systèmes "laissés à eux-mêmes" sont dits isolés ou pseudo-isolés. On peut utiliser ces objets isolés ou pseudo-isolés pour faire des référentiels particuliers dits galiléens :
- Lorsque dans un référentiel, le principe d'inertie est valide alors il est galiléen
- Un référentiel galiléen est soit immobile, soit le mouvement rectiligne uniforme
- Deux référentiels galiléens sont forcément immobiles ou en translation rectiligne l'un par rapport à l'autre
Note : Quand le référentiel n’est pas précisé, c’est qu’il s’agit de la Terre.
La notion de vitesse ⚡️
Un objet en mouvement est aussi caractérisé par sa vitesse. La vitesse est une grandeur physique qui est définie par une évolution face au temps.
En règle générale, une vitesse est égale à la division de la mesure d’une variation telle qu’une longueur, un volume ou encore un poids par la mesure du temps écoulé au cours de cette variation.
L’exemple le plus simple est celui de la vitesse de déplacement. Il s’agit d’une distance divisée par un temps comme les mètres par seconde ou les kilomètres par heure.

Notion de vitesse moyenne : calculer une vitesse moyenne
La vitesse moyenne d’un point parcourant une distance d entre les instants t1 et t2 peut être calculée grâce à la relation suivante : 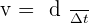
- où d est exprimée en mètre (m)
- Δt = t2 – t1 est exprimé en seconde (s )
- v est exprimé en mètre par seconde (m.s-1)
? La valeur de la vitesse moyenne d’un mobile entre deux instants est donc le quotient de la longueur parcourue entre les deux instants par la durée du parcours. Il est possible d’utiliser d’autres combinaisons d’unités pour exprimer une vitesse à condition qu’elles soient cohérentes entre elles. Par exemple si le temps est en minute et la distance en kilomètre alors la vitesse est en kilomètre par minute (km.m-1)
Dans le système international (SI), la vitesse cinématique est le mètre par seconde et se note m/s ou m.s-1
⏳ Or, dans le système usuel, on préférera, selon la situation et le mode de transport, le kilomètre par heure qui se note km/h ou km.h-1. En effet, dans la marine, on préférera plutôt le nœud, qui représente 0,5144 m/s.
Le système international des unités
L’ensemble des unités associées aux dimensions fondamentales constitue le système international d’unités. Il s’agit du système MksA (mètre, kilogramme, seconde, Ampère), mais le Kelvin, le mole et le candela font aussi partie de ce système. Ces unités sont appelées unités légales. Elles sont universelles et connues de par le monde entier.
Il est important de savoir que toutes les autres dimensions se déduisent de ces sept dimensions fondamentales par produit ou division de ces dimensions.
Dans certains sujets d’exercices, les grandeurs ne sont pas exprimées dans le système international mais avec des grandeurs usuelles. Il est facile de les comprendre et elles sont parfois utilisées dans la vie de tous les jours, mais il est essentiel de toujours effectuer les calculs avec les grandeurs exprimées dans l’unité internationale pour éviter les erreurs.
Calculer une distance ou une durée
Lorsque la vitesse est connue, cette expression peut être modifiée afin d’obtenir :
- La durée d’un trajet :
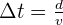
- La distance parcourue:
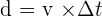
Convertir une vitesse
La formule qui exprime la vitesse peut également être utilisée pour convertir celle-ci... Pour passer d’une vitesse exprimée en kilomètre par heure à une vitesse en mètre par seconde. Si la vitesse a une valeur de v1 km.h-1 alors on peut considérer que cela correspond à une distance de v1 kilomètres parcourus en une heure.
- v1 km correspond à1000 x v1 m
- 1 heure correspond à 3600 s

- où v1 est une vitesse exprimée en kilomètre par heure
- v2 correspond à la même vitesse exprimée en mètre par seconde
✍️ En simplifiant on peut aussi écrire que v2 = v1 : 3,6 Par exemple si un point se déplace à une vitesse de 90 km.h-1 (90 x 1000)/3600 = 25 donc 90 km.h-1 correspond à 25 m.s-1. Pour passer d’une vitesse exprimée en mètre par seconde à une vitesse en kilomètre par heure. Si la vitesse a une valeur de v1 m.s-1 alors on peut considérer que cela correspond à une distance de v1 mètres parcourus en une seconde.
- v1 mètre correspond à v1/1000 kilomètre
- 1 seconde correspond à 1/3600 heure
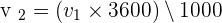
- v1 correspond à la même vitesse exprimée en mètre par seconde (m.s-1)
- v2 est une vitesse exprimée en kilomètre par heure (km.h-1)
En simplifiant on peut écrire v2 = v1 x 3,6 Par exemple si un point se déplace à une vitesse de 12,4 m.s-1 : (12,4 x 3600)/ 1000 = 44,64 donc 12,4 m.s-1 correspond à 44,64 km.h-1 .
| Vitesse en km/h | Vitesse en m/s |
|---|---|
| 90 km/h | 25 m/s |
| 120 km/h | 33 m/s |
| 130 km/h | 36 m/s |
Rappel concernant l'évolution de la vitesse au cours du temps
⏰ Au cours du temps les réactifs disparaissent donc leur concentration diminue. Or nous avons déjà vu que la concentration des réactifs est un facteur cinétique. Plus la concentration des réactifs est faible plus la réaction est lente. Donc, en général, au cours du temps la vitesse de réaction diminue.
- Si, pour un même intervalle de temps, la distance parcourue par le mobile est de plus en plus grande, sa vitesse augmente. On dit alors du mouvement qu'il est accéléré.
- Si, pour un même intervalle de temps, la distance parcourue par le mobile est constante. On dit que le mouvement est uniforme.
- Si, pour un même intervalle de temps, la distance parcourue est de plus en plus petite, sa vitesse diminue. On dit donc que le mouvement est ralenti.
La vitesse moyenne
La vitesse moyenne se calcule grâce au quotient de la distance L parcourue par la durée T mise à la parcourir. On a donc 
où la longueur de l’arc AB est notée L
La vitesse instantanée
La vitesse instantanée correspond à la vitesse du mobile à l’instant t. Elle peut être assimilé à la vitesse moyenne du mobile durant un intervalle de temps très court dt. On a donc 
Le vecteur vitesse 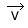
- sa direction : celle de la tangente à la trajectoire en M
- son sens : celui du mouvement
- sa valeur : valeur de la vitesse instantanée à l’instant t
- son origine : le point M
Notons qu'il est possible de la calculer grâce à la formule suivante 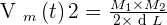
- Lors d'un mouvement rectiligne uniforme, le vecteur vitesse d’un point mobile est constant. Sa valeur, sa direction et son sens restent les mêmes à chaque instant..
- Lors d'un mouvement rectiligne varié, le vecteur vitesse garde la même direction mais les distances parcourues par le point mobile pendant des durées égales sont différentes.
- Une trajectoire correspond à un cercle dont le plan est orthogonal à l’axe fixe
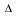
- La vitesse angulaire moyenne se définit ainsi : Soit un point M décrivant une trajectoire circulaire de rayon R. Un rayon du cercle balaie un angle
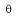
La vitesse angulaire moyenne peut se calculer grâce à l'expression suivante 
- La vitesse angulaire instantanée correspond à la vitesse angulaire à un instant donné. C’est le quotient du petit angle d θ balayé par un temps très court dt :
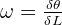 avec ω en rad/sd et θ en raddt en s
avec ω en rad/sd et θ en raddt en s
Il est tangent à la trajectoire au point considéré donc perpendiculaire au rayon. Son sens est celui du mouvement. Sa valeur est celle de la vitesse linéaire instantanée en ce point.
? Le point M décrit un arc AB pendant la durée t. Le rayon OM = R balaie l’angle q. Donc l’arc AB est égal à rq.
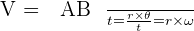
- La période, notée T, est l’intervalle de temps séparant 2 passages du mobile au même point et dans le même sens :
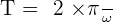 . La période s’exprime en seconde et la vitesse angulaire en rad/s
. La période s’exprime en seconde et la vitesse angulaire en rad/s - La fréquence, notée f, est le nombre de tours effectués par le mobile en une seconde :
 . La fréquence s’exprime en Hertz (Hz).
. La fréquence s’exprime en Hertz (Hz).
La vitesse moyenne d’un véhicule ne renseigne par sur le déroulement du trajet qui peut être jalonné de feux rouges, de ralentisseurs… Ainsi la vitesse moyenne ne donne qu’une information globale sur le trajet.
Afin de respecter les limitations de vitesse, le conducteur doit connaître la valeur de la vitesse instantanée (vitesse pour chaque instant t).
La vitesse instantanée d’un mobile à l’instant t est donc une vitesse moyenne pendant un temps très court. Cette vitesse est notée :
V = dL/dT
Le vecteur vitesse
? Le vecteur vitesse d’un point mobile se déplaçant sur une trajectoire est caractérisé par :
- Une direction
- Un sens
- Une valeur
- Une origine
Pour un mouvement rectiligne uniforme, le vecteur vitesse est constant, pour un mouvement rectiligne varié les distances parcourues pendant des durées égales sont différentes.
Cas particuliers de mouvements
Le mouvement rectiligne uniforme: il s’effectue suivant une droite à vitesse constante
Le mouvement circulaire uniforme: il s’effectue suivant une trajectoire circulaire à vitesse constante
Lorsque la vitesse varie régulièrement (comme une fonction affine du temps) on parle alors de mouvement uniformément varié.
Le centre d'inertie ?

En physique, on appelle inertie d'un corps, dans un référentiel galiléen, une tendance de ce corps à conserver sa vitesse. En effet, lorsqu'il y a absence d'influences extérieures, on parle aussi de forces extérieures, alors tout corps que l'on considère comme ponctuel va perdurer dans un mouvement rectiligne uniforme.
Notons que l'on appelle aussi l'inertie, principe d'inertie ou encore loi d'inertie. Puis, lorsque Newton est arrivé, on l'appelle également première loi de Newton.
Le principe d'inertie
Le principe d’inertie a été introduit par le célèbre Isaac Newton dans son ouvrage Philosophiae naturalis principia mathematica publié en 1687 et qui porte le nom de la première loi de Newton:
« Tout corps persévère dans l’état de repos ou de mouvement uniforme en ligne droite dans lequel il se trouve, à moins que quelque force n’agisse sur lui, et ne le contraigne à changer d’état »
Cela signifie concrètement qu’un système est nécessairement immobile ou en mouvement rectiligne uniforme si les forces du système se compensent.
Le principe d'inertie vu par Galilée
?? Galilée a énoncé le principe d'inertie de la façon suivante :
- Pour un observateur terrestre tout objet limité à lui-même persévère à son état de repos ou est rectiligne uniforme (mouvement) si les forces qui s'exercent sur lui se compensent.
- Réciproquement si toutes les forces qui s'exercent sur lui se compensent alors cet objet est au repos ou en mouvement rectiligne uniforme.
Ce principe établit par Galilée a été repris par Newton comme un principe fondamentale de sa théorie mécanique. Il s'agit de la première loi de Newton.
?? En physique, on appelle inertie d'un corps, dans un référentiel galiléen, une tendance de ce corps à conserver sa vitesse. En effet, lorsqu'il y a absence d'influences extérieures, on parle aussi de forces extérieures, alors tout corps que l'on considère comme ponctuel va perdurer dans un mouvement rectiligne uniforme.
Notons que l'on appelle aussi l'inertie, principe d'inertie ou encore loi d'inertie. Puis, lorsque Newton est arrivé, on l'appelle également première loi de Newton.
Elle s'énonce ainsi :
Un système isolé ou pseudo-isolé initialement au repos ou en mouvement rectiligne uniforme demeure dans son état.
On appelle référentiel galiléen tout référentiel au sein duquel le principe d'inertie est vérifié
Même s'il n'existe aucun référentiel galiléen au sens strict. Il est cependant possible de considérer certains référentiels usuels comme galiléen si certaines conditions sont vérifiée :
- Ainsi, le référentiel terrestre peut être considéré galiléen si on considère un mouvement dont la durée ne dépasse pas quelques minutes dans le but de s'affranchir du mouvement de rotation propre de la Terre.
- Le référentiel géocentrique peut également être considéré comme étant galiléen si on considère un mouvement dont la durée ne dépasse quelques heures dans le but de s'affranchir du mouvement de rotation de la Terre autour du Soleil.
- Le référentiel héliocentrique peut aussi être considéré comme étant galiléen car l'impact du mouvement de rotation du Soleil au sein de la galaxie est négligeable.
Inertie appliquée au mouvement
? Le principe d’inertie permet d’expliquer que le mouvement d’un corps dépend des forces qui lui sont appliquées. Tout les corps tendent à être immobiles ou en mouvement rectiligne uniforme. Si des forces agissent sur le corps, alors il résiste d’autant plus au changement que sa masse est élevée.
⚠️ À noter : la description du mouvement d’un objet entier peut s’avérer complexe et pour simplifier on se limite souvent à l’étude de la trajectoire d’un point particulier de cet objet appelé centre d’inertie et noté G. Lorsqu’un objet à une composition homogène alors G correspond au centre géométrique de cet objet.
Un exemple : le curling
? Le curling est un sport olympique (depuis 1924 !) d’origine écossaise. C’est un sport très ancien (qui remonte au XVIeme siècle) qui était pratiqué sur des étendues d’eau gelées. Le but du jeu est de placer une pierre de granite de près de 20 kilos le plus près possible d’une cible en la faisant glisser.
On surnomme le curling « roaring game » car la pierre émet un grondement caractéristique quand elle est en mouvement sur la glace. En France, le sport a même été surnommé « la pétanque sur glace ».
Résumer avec l'IA :






















Si vous désirez une aide personnalisée, contactez dès maintenant l’un de nos professeurs !
J’ai trouvé ce que je cherchais ça m’a vraiment aidé je vous remercie beaucoup et si je peux avoir une application sur ce site ça serait mieux pour moi et pour d’autres utilisateurs aussi
Comment peut-on trouver la trajectoire si x=lnt et y= 1 +1/t
Bonjour Camara ! Merci pour votre retour. Bonne journée ! :)
Je suis très content
Ce site est genial
Votre cours est formidable j’adore
Bonjour, nous serions ravis de vous aider ! Rendez-vous sur la plateforme de Superprof, sélectionnez la rubrique « Découvrir nos Superprofs » en indiquant la matière désirée. Vous trouverez de nombreux professeurs près de chez vous. :)
bonjour je voulais savoir quel est la difference entre un ingnieur genie mecanique et un mecanicien?
aussi connaissez vous un site uavec des cours en ingegneurie?
Merci, pour le service rendu.