Chapitres
- Les champs
- Le principe de superposition
- Le théorème de Gauss
- Loi de Coulomb
- Le but de l'électromagnétisme
- Symétries du champ électromagnétique
- Équation locale de conservation de la charge
- Contenu physique des équations de Maxwell
- Résolution des équations de Maxwell
- Relations de discontinuités
- Équation locale de Poynting
- Cas particulier du régime statique
- Cas particulier du régime stationnaire
- Cas particuliers des régimes lentement variables : Approximation des régimes quasi-stationnaires
Les champs
Champ électrique
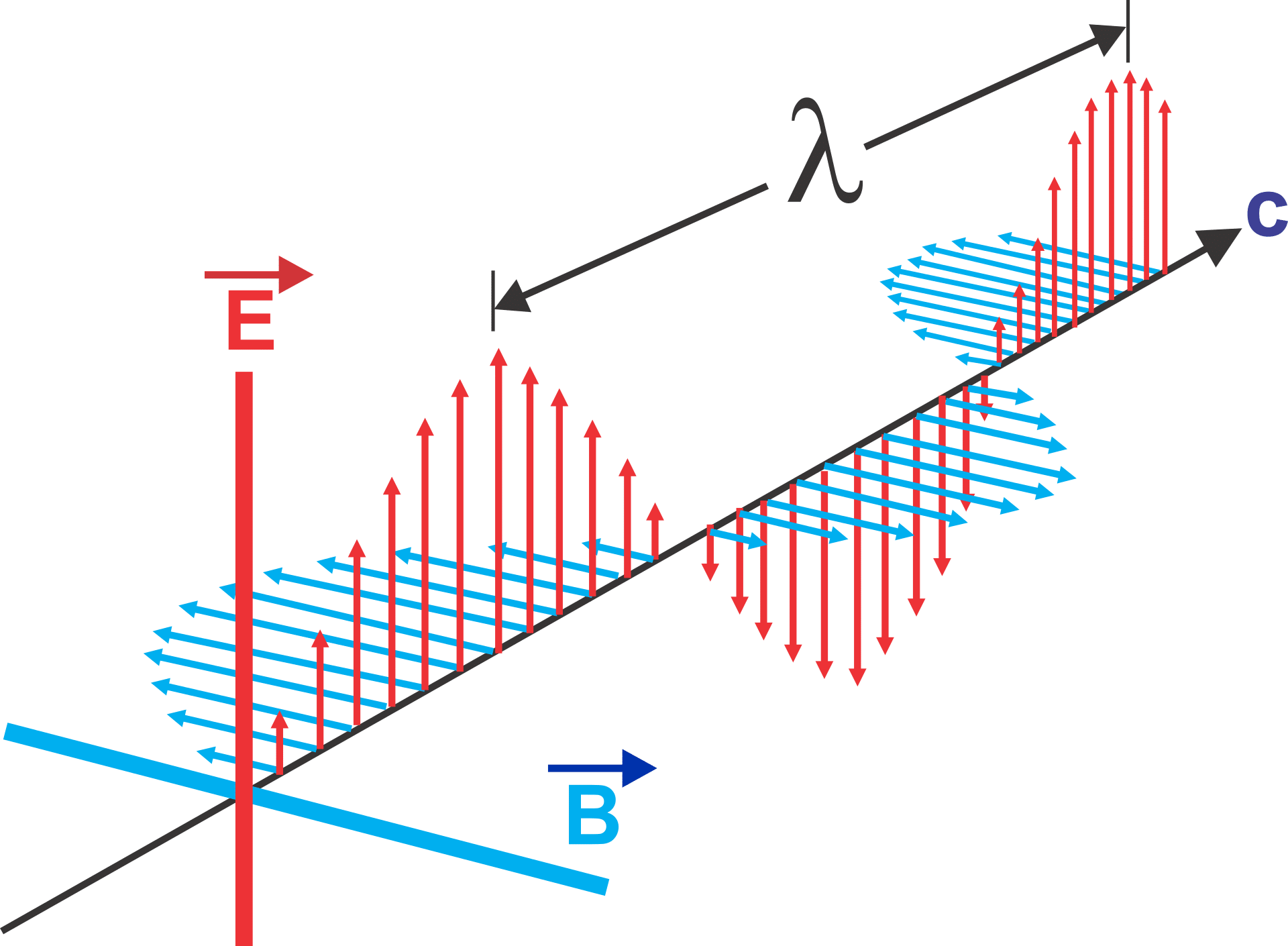
En physique, on appelle champ électrique tout champ vectoriel créé par des particules électriquement chargées. Plus exactement, lorsque nous sommes en présence d'une particule chargée, les propriétés locale de l'espace défini sont alors modifié ce qui permet de définir la notion de champ. En effet, si une autre charge se trouve être dans le dit champ, elle subira ce qu'on appelle l'action de la force électrique qui est exercée par la particule malgré la distance. On dit alors du champ électrique qu'il est le médiateur de la dite action à distance.
Si on se veut plus précis, on peut définir dans un référentiel galiléen défini, une charge q définie de vecteur vitesse v qui subit de la part des autres charges présentes, qu'elles soient fixes ou mobiles, une force qu'on définira de force de Lorentz. Cette force se décompose ainsi :
![\[ \overrightarrow { f } = q \left ( \overrightarrow { E } + \overrightarrow { v } \wedge \overrightarrow { B } \right) \]](https://www.superprof.fr/ressources/wp-content/ql-cache/quicklatex.com-2b36c8f8a0e4e4457d77abd7f3551768_l3.png "Rendered by QuickLaTeX.com")
avec :
-
![\[ \overrightarrow { E } \]](https://www.superprof.fr/ressources/wp-content/ql-cache/quicklatex.com-53ace61d3bf0a0828a2ff369f23b6ca8_l3.png "Rendered by QuickLaTeX.com")
le champ électrique. Celui-ci décrit dans ce cas la partie de la force de Lorentz qui est indépendante de la vitesse de la charge
-
![\[ \overrightarrow { B } \]](https://www.superprof.fr/ressources/wp-content/ql-cache/quicklatex.com-a7e287ba2f5386d717a282b10c5fec88_l3.png "Rendered by QuickLaTeX.com")
le champ magnétique. Celui-ci décrit ainsi la partie de la force exercée sur la charge qui dépend du déplacement de cette même charge dans le référentiel choisi.
De plus, il est important de noter que les deux champs, électrique et magnétique, dépendent du référentiel d'étude.
Avec cette formule, on peut alors définir le champ électrique comme étant le champ traduisant l'action à distance subie par une charge électrique fixe dans un référentiel défini de la part de toutes les autres charges, qu'elles soient mobiles ou fixes.
Mais on peut également définir le champ électrique comme étant toute région de l'espace dans laquelle une charge est soumise à une force dite de Coulomb.
On commence à parler de champ électrostatique lorsque, dans un référentiel d'étude, les charges sont fixes. Notons d'ailleurs que le champ électrostatique ne correspond pas au champ électrique comme décrit plus haut dans cet article puisqu'en effet, lorsque les charges sont en mouvement dans un référentiel, il faut ajouter à ce référentiel un champ électrique qui est induit par les déplacement des charges afin d'obtenir un champ électrique complet.
Mais, le champ électrique reste dans la réalité un caractère relatif puisqu'il ne peut exister indépendamment du champ magnétique. En effet, si on observe la description correcte d'un champ électromagnétique, celui-ci fait intervenir un tenseur quadridimensionnel de champ électromagnétique dont les composantes temporelles correspondent alors à celle d'un champ électrique. Seul ce tenseur possède un sens physique. Alors, dans le cas d'un changement de référentiel, il est tout à fait possible de transformer un champ magnétique en champ électrique et inversement.
Le champ électromagnétique
En physique, on appelle champ électromagnétique la représentation dans l'espace d'une force électromagnétique exercée par des particules chargées. Ce champ représente alors l'ensemble des composantes de la force électromagnétique qui s'appliquent à une particule chargée qui se déplace alors dans un référentiel galiléen.
On peut alors définir la force subit par une particule de charge q et de vecteur vitesse par l'expression suivante :
avec :
![\[ \overrightarrow { E } \]](https://www.superprof.fr/ressources/wp-content/ql-cache/quicklatex.com-2ec0e5489488c8c138a40be4f6803b9e_l3.png "Rendered by QuickLaTeX.com")
le champ électrique. Celui-ci décrit dans ce cas la partie de la force de Lorentz qui est indépendante de la vitesse de la charge
![\[ \overrightarrow { B } \]](https://www.superprof.fr/ressources/wp-content/ql-cache/quicklatex.com-f25ebaab0b6d1d844b6c46abbe39dbdc_l3.png "Rendered by QuickLaTeX.com")
le champ magnétique. Celui-ci décrit ainsi la partie de la force exercée sur la charge qui dépend du déplacement de cette même charge dans le référentiel choisi.
En effet la séparation de la partie magnétique et de la partie électrique de dépend que du point de vue pris selon le référentiel d'étude.
De plus, il peut être intéressant de savoir que les équations de Maxwell régissent les deux composantes couplées, c'est à dire électrique et magnétique, de sorte que toute variation d'une composante induira la variation de l'autre composante.
D'ailleurs, le comportement des champs électromagnétiques se trouve décrit de façon classique par les équations de Maxwell et de manière plus générale par l'électrodynamique quantique.
La façon la plus utilisée afin de définir le champ électromagnétique est celle du tenseur électromagnétique de la relativité restreinte.
Le champ électrostatique
On parle de champ électrostatique lors que les charges qui constitue le champ sont au repos dans le référentiel d'étude. Ce champ est donc déduit de l'expression de la loi de Coulomb, aussi appelée interaction électrostatique.
Le champ gravitationnel
En physique classique, on appelle champ gravitationnel, ou encore champ de gravitation, un champ qui est réparti dans l'espace et dû à la présence d'une masse qui est alors susceptible d'exercer une influence gravitationnelle sur tout les autres corps pouvant être présent à proximité immédiate ou non.
On peut démontrer que le champ gravitationnel créé en un point quelconque par un corps ponctuel dérive d'un potentiel scalaire dit newtonien.
En physique classique, le champ gravitationnel ou champ de gravitation est un champ réparti dans l'espace et dû à la présence d'une masse susceptible d'exercer une influence gravitationnelle sur tout autre corps présent à proximité (immédiate ou pas). L'introduction de cette grandeur permet de s'affranchir du problème de la médiation de l'action à distance apparaissant dans l'expression de la force de gravitation universelle.
On peut interpréter le champ gravitationnel comme étant la modification de la métrique de l'espace-temps. L'approximation newtonienne est alors valable uniquement dans le cas où les corps présentent une vitesse faible par rapport à celle de la lumière dans le vide et si le potentiel gravitationnel qu'ils créent est tel que le quotient du potentiel gravitationnel sur le carré de la vitesse de la lumière dans le vide est négligeable.
On peut approcher le champ électrique et le champ gravitationnel. En effet, l'expression du champ et du potentiel ne sont différents que d'une constante. De plus, les principaux théorèmes de calculs, celui de la superposition ou de Gauss par exemple, peuvent s'appliquer dans les deux cas. Ce qui les différencie alors est le caractère attractif, donc entre deux charges de signe opposé, ou répulsif, donc entre deux charges de même signe, du champ électrique tandis que le champ gravitationnel ne peut être qu'attractif.
Les équations de Maxwell
Les équations de Maxwell-Gauss, aussi connues sous le noms d’équations de Maxwell-Lorenz sont des équations fondamentales de la physique. En effet, ces sont elles qui régissent l’électromagnétisme. Elles tiennent leur nom du physicien James Clerk Maxwell d’origine écossaise. Toute sa vie il a travaillé sur les champs électriques et magnétiques et il a également contribué à l’élaboration de nombreuses lois physiques dans son domaine. Il est considéré comme l’un des scientifiques les plus influents du IXXème siècle.
Elle réunit sous la forme d’équations intégrales des lois déjà connues telles que celles de théorèmes de Gauss, Ampère et Faraday.
Les équation de Maxwell sont essentielles puisqu’elles démontrent qu’en régime stationnaire, les champs électrique et magnétiques sont indépendants l’un de l’autre, ce qui n’est pas nécessairement le cas lorsque l’on se trouve en régime variable. En effet, dans le cas le plus général, il faut alors parler du champ électromagnétique puisque la séparation entre l’électrique et le magnétique n’est qu’un aspect visualisé par l’Homme.
Le principe de superposition
Il est possible d'appliquer le principe de superposition à un système de type entrée-sortie si :
- La somme de deux entrées quelconque correspond à la somme des deux sorties correspondantes ;
- Un multiple d'une entrée quelconque correspond le même multiple de la sortie correspondante.
Dans ce cas, c'est-à-dire celui d'un système physique, on peut appeler l'entrée excitation et la sortie réponse.
On obtient alors, en notant les excitations ƒ et les réponses x (donc les mouvements généré par les forces mécaniques ƒ) :
- Lorsque l'on sollicite le système par une entrée, donc une excitation notée ƒ1, une réponse, donc un déplacement, qui sera noté x1 ;
- Lorsque l'on sollicite le système par une entrée, donc une excitation notée ƒ2, une réponse, donc un déplacement, qui sera noté x2 .
Le théorème de Gauss
Le théorème de Gauss permet, en électromagnétisme, de calculer le flux d'un champ électrique à travers une surface qui est fermée et ce grâce à la connaissance des charges électriques que cette surface renferme.
Il s'énonce ainsi :
Le flux du champ électrique à travers une surface S fermée est égal à la somme des charges électriques contenues dans le volume V délimité par cette surface, divisée par la permittivité du vide.
Loi de Coulomb
Coulomb, un physicien français, a établi en 1758 que le champ doit varier comme le carré inverse de la distance entre les charges à une précision de 0,02 sur l'exposant avec l'aide d'un dispositif appelé balance de Coulomb. Cette balance est constituée d'un fil de torsion en argent sur lequel est fixé des matériaux chargés. Ainsi, la loi d'attraction entre deux charges ponctuelles notées q1 et q2 , fixes dans le référentiel défini et séparées par une distance r, se définit ainsi :
- La force est dirigée selon la droite reliant les deux charges ;
- Elle est attractive si les charges sont de signes opposée et répulsive sinon ;
- Son intensité est proportionnelle aux valeurs de q1 et q2 et varie en raison inverse du carré de la distance r.
Il est alors possible de traduire ces caractéristiques en une formule exprimant la force exercée par q1 sur q2 :
![\[ \overrightarrow{ f _ { e } } = \frac { 1 } { 4 \pi \epsilon _ { 0 } } \frac { q _ { 1 } q _ { 2 } }{ r ^ { 2 } } \overrightarrow { e _ { r } } \]](https://www.superprof.fr/ressources/wp-content/ql-cache/quicklatex.com-5d8b769efb0e4b6de0856be8f43f916e_l3.png "Rendered by QuickLaTeX.com")
avec :
-
![\[ \overrightarrow { e _ { r } } \]](https://www.superprof.fr/ressources/wp-content/ql-cache/quicklatex.com-67dc8cad4bef9e1bc838fb874627c0f5_l3.png "Rendered by QuickLaTeX.com")
le vecteur unitaire de la droite reliant q1 et q2 qui est dirigée dans le sens 1 vers 2
-
![\[ \epsilon _ { 0 } \]](https://www.superprof.fr/ressources/wp-content/ql-cache/quicklatex.com-c29caf22245c9f18785c5ce023a6cd3e_l3.png "Rendered by QuickLaTeX.com")
la permittivité diélectrique du vide
Ce qui peut rendre la compréhension de cette formule compliquée est la notion de force à distance. En effet, comment une charge peut savoir qu'une autre charge ponctuelle se trouve à une certaine distance d'elle et alors exercer sur force sur cette charge en fonction de la distance qui les sépare.
Dans ce cas, tout comme pour un champ gravitationnel, il peut être utile de séparer dans la loi de force ce qui dépend de la charge subissant la force et donc d'obtenir la relation suivante :
![\[ \begin{cases} \overrightarrow { f } = q _ { 2 } \left[ \frac { 1 } { 4 \pi \epsilon _ { 0 } } \frac { q _ { 1 } } { r ^ { 2 } } \overrightarrow { e _ { r } } \right] = q _ { 2 } \overrightarrow { E } \\ \overrightarrow{ E } = \frac { 1 } { 4 \pi \epsilon } \frac { q _ { 1 } }{ r ^ { 2 } } \overrightarrow { e _ { r } } \end{cases} \]](https://www.superprof.fr/ressources/wp-content/ql-cache/quicklatex.com-12e87b1b058783c35e24ad9c99272f55_l3.png "Rendered by QuickLaTeX.com")
avec :
-
![\[ \overrightarrow { E } \]](https://www.superprof.fr/ressources/wp-content/ql-cache/quicklatex.com-0acd56f664b08246f25655cb4106202c_l3.png "Rendered by QuickLaTeX.com")
un champ électrique électrostatique créé à partie de la charge q1 au point où se trouve la seconde charge q2
Ainsi, avec cette relation, il est plus aisé d'interpréter l’existence d'une force à distance. En effet, la charge considérée comme "source", c'est-à-dire q1, crée en tout point de l'espace un champ électrique dont la forme est donnée par la relation exprimée ci-dessus, et une charge quelconque considérée comme "test" subira l'effet de ce champ sous la forme d'une force égale au produit de cette charge par le champ électrostatique. Dans ce cas, ce champ électrostatique apparaîtra comme la force entre deux particules ponctuelles fixes par unité de charge.
Le but de l'électromagnétisme
- But de l'électromagnétisme : Décrire l'action d'une distribution de charges sur une autre.
- Utilisation d'un intermédiaire qu'est le champ électromagnétique. Il faut donc savoir
- déterminer le champ créé par une distribution de charges
- déterminer l'action subie par l'autre distribution dans ce champ.
- Le champ magnétique n'est pas un simple intermédiaire de calcul. C'est une entité physique à part entière comme le montre l'étude des phénomènes de propagation.
Description du champ créé par une distribution de charges
- Il est défini par les équations de Maxwell.
- Les équations de Maxwell sont linéaires : on a donc le théorème de superposition des solutions.
- En régime quelconque, les équations de Maxwell sont couplées: le champ électromagnétique forme un tout indissociable.
Actions subies par une distribution de charges
- Par une charge ponctuelle : force de Lorentz.
- Par une distribution volumique de charges.
- Par un conducteur parcouru par un courant : force de Laplace.
- Par un dipôle électrique : expression de la résultante et du moment résultant.
- action principale: tendance à l'alignement dans le champ électrique. (évident)
- action secondaire: tendance à se déplacer vers les zones de champ fort. (évident)
- Par un dipôle magnétique: expression de la résultante et du moment résultant. (évident)
- action principale: tendance à l'alignement dans le champ magnétique. (évident)
- action secondaire: tendance à se déplacer vers les zones de champ fort.
Symétries du champ électromagnétique
- Un plan est un plan de symétrie d'un problème si les sources du champ restent inchangées lorsqu'on effectue la symétrie par rapport à ce plan.
- Un plan est un plan d'antisymétrie d'un problème si les sources du champ sont inversées (changement de signe pour les charges, de sens pour les courants) lorsqu'on effectue la symétrie par rapport à ce plan.
- Le champ électrique est un vrai vecteur donc
- en tout point d'un plan de symétrie des charges, le champ électrique est dans ce plan,
- en tout point d'un plan d'antisymétrie, le champ électrique est orthogonal à ce plan.
- Le champ magnétique est un pseudovecteur donc
- en tout point d'un plan de symétrie des courants, le champ magnétique est orthogonal à ce plan,
- en tout point d'un plan d'antisymétrie, le champ magnétique est dans ce plan.
Invariances des sources
Mêmes résultats qu’en électrostatique et en magnétostatique !
Plan de symétrie ou d’antisymétrie des sources
Un plan est un plan de symétrie des sources du champ si elles restent inchangées lorsqu'on effectue la la symétrie par rapport à ce plan.
Un plan est un plan d'antisymétrie des sources du champ si elles sont inversées (changement de signe pour les charges, de sens pour les courants) lorsqu'on effectue la symétrie par rapport à ce plan.
En tout point d'un plan de symétrie des sources, le champ électrique est contenu dans ce plan et le champ magnétique est orthogonal à ce plan.
En tout point d'un plan d'antisymétrie des sources, le champ magnétique est contenu dans ce plan et le champ électrique est orthogonal à ce plan.
Équation locale de conservation de la charge
Intensité électrique
- Par définition, c'est un débit de quantité de charge à travers une surface orientée.
- Par le calcul, on obtient le flux du vecteur densité de courant à travers cette surface. Remarque: l'intensité dépend donc de la surface.
Bilan de conservation de la charge
- Formulation intégrale.
- Équation locale de conservation.
Contenu physique des équations de Maxwell
Équation de Maxwell - Gauss
- Théorème de Gauss.
- Le champ électrique est à flux conservatif en dehors des charges : le champ augmente donc quand les lignes de champ se resserrent.
Équation de Maxwell- Ampère
- Théorème d'Ampère.
Équation du flux magnétique
- Les lignes de champ ne peuvent ni converger en un point, ni diverger d'un point.
- Le champ magnétique est à flux conservatif : le champ augmente donc quand les lignes de champ se resserrent, et on peut définir le flux du champ magnétique à travers un contour.
Équation de Maxwell - Faraday
- Loi de Faraday
Résolution des équations de Maxwell
Introduction des potentiels
- Introduction du potentiel scalaire électrique et du potentiel vecteur magnétique.
- L'introduction des potentiels a pour but de découpler les équations de Maxwell.
Choix d'une jauge
- Le choix du couple potentiel scalaire électrique - potentiel vecteur magnétique n'est pas unique.
- On peut imposer une condition supplémentaire entre ces deux potentiels : on utilise la jauge de Lorentz.
- Les deux potentiels vérifient alors des équations du même type découplées
Relations de discontinuités
Discontinuité du champ électrique
- En présence de répartitions volumiques de charges dans l'espace, le champ électrique et son potentiel sont continus dans tout l'espace.
- Les discontinuités éventuelles sont dues aux modélisations mathématiques des répartitions de charges.
- Rappel des modélisations surfaciques et linéiques de répartition de charges.
- Les discontinuités éventuelles du champ électrique et de son potentiel n'existent qu'au niveau de ces répartitions de charges modélisées.
- Pour une répartition surfacique de charges :
- le champ électrique est discontinu à la traversée de cette surface,
- le potentiel électrique est continu.
- Pour une répartition linéique de charges :
- le champ électrique est discontinu,
- le potentiel est discontinu.
- Relations de passage du champ électrique à la traversée d'une surface chargée.
Discontinuité du champ magnétique
- En présence de répartitions volumiques de courants dans l'espace, le champ magnétique et son potentiel vecteur sont continus dans tout l'espace.
- Les discontinuités éventuelles sont dûes aux modélisations mathématiques des répartitions de courant.
- Rappel des modélisations surfaciques et linéiques de répartition de courants.
- Les discontinuités éventuelles du champ magnétique et de son potentiel vecteur n'existent qu'au niveau de ces répartitions de courants modélisées.
- Pour une répartition surfacique de courants :
- le champ magnétique est discontinu à la traversée de cette surface,
- le potentiel vecteur magnétique est continu.
- Pour une répartition linéique de courants :
- le champ magnétique est discontinu,
- le potentiel vecteur est discontinu.
- Relations de passage du champ magnétique à la traversée d'une répartition surfacique de courants.
Équation locale de Poynting
Signification physique
- Expression de la puissance fournie par un champ électromagnétique à des porteurs de charge libres : en retenant que la force magnétique ne travaille pas, que la force électrique est proportionnelle à la charge et que la puissance reçue dépend de la vitesse, il est clair que l' expression de la puissance va faire intervenir le champ électrique et le vecteur densité de courant.
- Passage à la loi de Joule macroscopique pour une portion de conducteur.
- Densité volumique d'énergie électromagnétique: on admet que chaque élément de volume de l'espace contient une énergie potentielle (donc récupérable) de par la présence d'un champ électrique et d'un champ magnétique.
- Vecteur de Poynting: on admet que la direction du vecteur de Poynting donne la direction de propagation de l'énergie électromagnétique, et le flux du vecteur de Poynting à travers une surface représente le débit d'énergie à travers cette surface, c'est à dire l'énergie qui traverse la surface par unité de temps, c'est à dire la puissance qui traverse la surface.
- Bilan énergétique.
- Analogie avec l'équation de conservation de la charge.
Cas particulier du régime statique
Simplification des équations
- Ce sont les charges qui créent le champ qui sont statiques, pas celles qui le subissent.
- Équations de Maxwell :
- Seul le champ électrique existe (on le nomme champ électrostatique).
- Typographie du champ électrique :
- Les lignes de champ peuvent diverger d'un point: il y a alors une charge ponctuelle positive en ce point.
- Les lignes de champ peuvent converger vers un point : il y a alors une charge ponctuelle négative en ce point.
- Il n'existe donc pas d'extremum du potentiel en dehors des charges.
- En dehors des charges, le champ augmente quand les lignes de champ se resserrent.
- Les lignes de champ ne se referment pas sur elles-même.
- Relations de passage.
- Résolution des équations de Maxwell :
- introduction du potentiel.
- Équation de Poisson.
- Solution en l'absence de charges à l'infini et en prenant le potentiel nul à l'infini.
- Passage au champ électrique : loi de Coulomb.
Exemples de calculs de champs électriques
- Calcul par le théorème de Gauss quand les symétries sont suffisantes : c'est la méthode à essayer en premier.
- Calcul par la loi de Coulomb : intégrale vectorielle donc trois intégrales scalaires à priori sauf si on détermine au préalable la direction du champ.
- Calcul à partir du potentiel : une seule intégrale scalaire mais il faut faire très proprement le passage au champ.
Cas particulier du régime stationnaire
Simplification des équations
- Les charges qui créent le champ sont en mouvement mais de façon stationnaire : le vecteur densité de courant est non nul mais indépendant du temps, les champs sont indépendants du temps.
- Équation locale de conservation de la charge :
- Le vecteur densité de courant est à flux conservatif donc le courant est identique en tout point d'un fil.
- Loi des nœuds .
- On peut définir l'intensité à travers un contour.
- Équations de Maxwell :
- Les deux champs électrique et magnétique existent mais sont découplés.
- La détermination du champ électrique à partir des charges est identique au cas de l'électrostatique.
- Théorème d'Ampère : on peut définir le courant qui traverse un contour.
- Typographie du champ magnétique :
- les lignes de champ peuvent se refermer sur elles-même: elles enlacent alors des courants et leur orientation est donnée par la règle du tire-bouchon.
- Les lignes de champ ne peuvent ni converger en un point, ni diverger d'un point.
- Le champ magnétique est à flux conservatif : le champ augmente donc quand les lignes de champ se resserrent.
- Relations de passage.
- Résolution des équations de Maxwell pour le champ magnétique :
- Introduction du potentiel vecteur.
- Jauge de Coulomb.
- Équation de Poisson pour le potentiel vecteur.
- Solution en l'absence de courants à l'infini et en prenant le potentiel nul à l'infini. (son utilisation est hors programme)
- Passage au champ magnétique: loi de Biot et Savart.
Exemples de calculs de champ magnétique et de force
- Calcul par le théorème d'Ampère quand les symétries sont suffisantes : c'est la méthode à essayer en premier.
- Calcul par la loi de Biot et Savart: intégrale vectorielle donc trois intégrales scalaires à priori sauf si on détermine au préalable la direction du champ.
- Calcul à partir du potentiel vecteur : intégrale vectorielle également donc pas plus simple (et hors programme).
Exemples de calcul de potentiel vecteur
- Peut servir pour calculer un flux, un champ électromoteur...
- Potentiel vecteur créé par un fil infini.
- Potentiel vecteur d'un champ uniforme.
Cas particuliers des régimes lentement variables : Approximation des régimes quasi-stationnaires
Définition de l'approximation.
- l'AROS consiste à négliger la propagation des champs électromagnétiques dans la portion d'espace étudiée.
En régime sinusoïdal, les variations spatiales des champs dues à la propagation ont pour période la longueur d'onde. Il suffit donc que la dimension de l'espace d'étude soit très inférieure à la longueur d'onde.
- Dans les équations de Maxwell, il suffira de faire tendre c (vitesse de la lumière dans le vide) vers l'infini.
- Dans la suite de ce cours, on se placera dans l'approximation des régimes quasi-stationnaires.
Conséquences.
- Équations de Maxwell :
- Les deux champs électrique et magnétique existent et sont couplés.
- La détermination du champ magnétique à partir des courants est identique au cas de la magnétostatique.
- Équation locale de conservation de la charge :
- Le vecteur densité de courant est à flux conservatif donc le courant est identique en tout point d'un fil.
- Loi des nœuds.
- On peut définir l'intensité à travers un contour.
- Relations de passage.
- Résolution des équations de Maxwell :
- Introduction des potentiels.
- Équations de Poisson pour les potentiels.
- Solution en l'absence de courants à l'infini et en prenant les potentiels nuls à l'infini.
La plateforme qui connecte profs particuliers et élèves
Vous avez aimé cet article ? Notez-le !
Loading...
Si vous désirez une aide personnalisée, contactez dès maintenant l’un de nos professeurs !