Chapitres
L'écoulement laminaire
Généralités
Quand on parle d'écoulement laminaire en mécanique des fluides, on évoque le mode d'écoulement d'un fluide dans le cas où l'ensemble du fluide s'écoule plus ou moins dans la même direction et cela sans que les différences locales ne se contrarient. On est alors en opposition au régime turbulent au cours duquel l'écoulement produit des tourbillons qui vont mutuellement se contrarier. Ainsi, lorsque l'on cherche à faire circuler un fluide dans un tuyau, on cherche à mettre en place un écoulement laminaire afin qu'il y ait moins de pertes de charge. Mais on cherche aussi à mettre en place un écoulement laminaire lorsque l'on cherche à faire voler un avion afin que le vol soit stable et prévisible à l'aide d'équations.
L'écoulement laminaire d'un point de vue microscopique
L'écoulement laminaire d'un point de vue macroscopique
Tout comme la notion de régime turbulent, la notion de régime laminaire est très fortement liée à la viscosité du fluide en mouvement. En effet, lorsque le liquide se situe dans une conduite ou autour d'un obstacle, alors, au voisinage d'une paroi sur laquelle la vitesse relative du fluide est nulle, on peut alors observer l'apparition de fortes variations de vitesse au sein desquelles la viscosité est impliquée. De façon plus précise, on peut dire que l'écoulement visqueux est caractérisé grâce à un nombre sans dimension que l'on appelle le nombre de Reynolds. Ce nombre permet alors de mesurer l'importance relative des forces inertielles qui sont liées à la vitesse et des forces de frottement qui sont liées à la viscosité. Ainsi, si ces dernières sont prépondérantes, alors on peut dire que le frottement, qui se produit entre deux couches de fluides, maintient leur cohésion : on obtient ainsi un écoulement laminaire. Dans le cas où le nombre de Reynolds augmente au-delà d'un certain seuil, alors l'écoulement est déstabilisé. Dans ce cas, il peut y avoir un régime turbulent qui va se mettre en place après qu'une phase de transition, plus ou moins importante, ait eu lieu.
Le nombre de Reynolds
Le nombre de Reynolds, noté Re, correspond à un nombre sans dimension qui est utilisé en mécanique des fluides. Cette grandeur permet alors de caractériser un écoulement, en particulier la nature de son régime. Il est ainsi possible de savoir si un écoulement est laminaire, transitoire ou turbulent.
L'écoulement laminaire dans le cas d'un corps profilé dans l'air
La loi de Poiseuille
La loi de Poiseuille, que l'on appelle aussi loi de Hagen-Poiseuille, permet de décrire ce que l'on appelle écoulement laminaire, c'est à dire un écoulement sous la forme de filets de liquide parallèles, d'un liquide visqueux au sein d'une conduite cylindrique. On appelle logiquement écoulement de Poiseuille tout écoulement qui suit une loi de Poiseuille. De façon générale, la loi de Poiseuille permet de décrire de façon théorique la relation existant entre le débit d'un écoulement et la viscosité d'un fluide, mais aussi la différence de pression aux extrémités de la canalisation ainsi que la longueur et le rayon de cette même canalisation.
La viscosité
- La viscosité dynamique qui est la grandeur la plus utilisée. En effet, on se réfère généralement à cette grandeur lorsque l'on parle de viscosité sans précision. Elle permet de faire le lien entre la contrainte de cisaillement et le gradient transversal de la vitesse d'écoulement dans la matière. C'est donc pour cela que l'on appelle cette grandeur vitesse dynamique.
- La viscosité cinématique, cette grandeur peut être déduise de la vitesse dynamique ;
- La seconde viscosité qui caractérise la résistance du fluide à des variations de volume ;
- Et pour finir, la viscosité de volume qui correspond à la combinaison de la viscosité dynamique et la seconde viscosité.
De ce fait, on peut considérer la viscosité comme correspondant à une quantité tensorielle bien qu'il reste possible que, selon les cas, on puisse exprimer cette grandeur sous la forme d'une grandeur scalaire. La viscosité (de cisaillement) peut être vue comme la résistance à l'écoulement des différentes couches d'un fluide les unes sur les autres. Plusieurs grandeurs physiques caractérisent la viscosité: En ce qui concerne les liquides, alors que l'inverse est vrai pour les gaz, la viscosité va tendre, de façon générale, à diminuer lorsque la température va augmenter. De plus, croire que la viscosité d'un fluide donné augmente avec la densité est faux car ce n'est pas nécessairement vrai. On peut en effet prendre l'exemple de l'huile qui, pourtant moins dense que l'eau (0,92 pour l'huile de Colza à 20°C et 1 pour l'eau à 20°C) alors que l'huile est, de façon très nette, plus visqueuse que l'eau. Pour ce qui est des huiles de mécaniques, elles seront classer selon leur viscosité puisque l'huile utilisée dans les moteurs va varier selon les besoin de lubrifications de celui-ci mais aussi selon les température auxquelles l'huile mécanique sera soumise lorsque le moteur sera en marche.
La viscosité peut varier
Comme expliqué précédemment, la viscosité d'un fluide varie selon la température, mais aussi les actions mécaniques auxquelles ce fluide est soumis. Ainsi, afin de déterminer l'importance de l'effet de la température sur la viscosité d'un fluide, on va utilisé un indice appelé indice de viscosité. De façon logique, plus cet indice est grand, moins la température aura une influence sur la viscosité du fluide étudié.
La viscosité dynamique
La viscosité dynamique peut alors être définie en considérant deux couches d'un fluide que l'on nommera abcd et a'b'c'd' en sachant que la couche abcd est animée d'une vitesse relative à a'b'c'd' que l'on notera dv qui sera dirigée selon x. On considère également une force de frottement notée F comme s'exerçant sur la couche a'b'c'd' séparée de dz. Ainsi, la viscosité dynamique, que l'on note η ou µ, est présente au sein de la relation entre la norme de la force de frottement F et le taux de cisaillement dv/dz. On à obtient alors : [ F = eta times S times frac { text { d } v } { text { d } z } ] avec S correspondant à la surface de chaque couche de liquide. L'analyse dimensionnelle de la viscosité dynamique donne donc, de façon logique : [ left[ eta right] = left[ M right] times left[ L right] ^ { - 1 } times left[ T right] ^ { - 1 } ] Si on souhaite utiliser les unités du système international d'unité, la viscosité dynamique possède la pascals secondes, noté Pa.s, en unité. Auparavant, on utilisé le poiseuille, noté Pl, qui présentait la même valeur que le pascals secondes. Une ancienne unité du système CGS pour la viscosité dynamique était la poise, notée Po, donc la correspondance était : [ 1 text { Pa } cdot text { s } = 10 text { Po } ] Ainsi, la viscosité de l'eau à 20°C correspond à 1 centipoise, noté cPo, ce qui correspond à 1 mPa.s.
La fluidité
La fluidité correspond à l'inverse de la viscosité dynamique
La viscosité cinématique
Il est possible d'obtenir la viscosité cinématique, noté ν, en divisant la discosité dynamique par la masse volumique, notée ρ, du fluide. On obtient alors la relation suivante : [ nu = frac { eta } { rho } ] Son unité, le mètre carré par seconde, noté n².s-1, correspondant, dans l'ancien système CGS comme étant le stokes ou centistokes notés respectivement St et cSt. La conversion est très rapide car : [ 1 text { St } = 1 text { cm } ^ 2 cdot text { s } ^ { - 1 } = 10 ^ { - 4 } text { m } ^ 2 cdot text { s } ^ {- 1 } ] et [ 1 text{ cSt } = 1 text { mm } ^ 2 cdot text { s } ^ { - 1 } = 10 ^ { - 6 } text{ m } ^ 2 cdot text { s } ^ { - 1 } ]
La seconde viscosité
La seconde viscosité correspond au second paramètre scalaire qui permet de caractériser de façon complète un fluide considéré comme étant newtonien. Elle est cependant omise dans la littérature puisque, pour la plupart des fluides usuels, il manque la caractérisation des fluides en ce qui concerne leur approximation newtonienne.
La viscosité de volume
La viscosité de volume correspond à une fonction linéaire des viscosités principale et seconde viscosité. On a ainsi : [ 3 times K = 3 times lambda + 2 times mu ]
La viscosité élongationnelle
On considère la viscosité élongationnelle comme étant une viscosité qui apparaît lorsqu'une contrainte élongationnelle s'applique au fluide étudié.
Le régime turbulent
Le terme turbulence correspond à l'état de l'écoulement d'un fluide, qu'il soit liquide ou gaz, au sein duquel la vitesse présente un caractère tourbillonnaire. On entend par là la présence de tourbillons dont la taille, la localisation mais également l'orientation vont, de façon constante, varier. On peut caractériser un écoulement turbulents par une apparence très désordonnée mais également par un comportement qui restera difficilement prévisible et par l'existence de nombreuses échelles spatiales et temporelles. Il est possible de voir apparaître ce type d'écoulement dans le cas où la source d'énergie cinétique, qui provoque la mise en mouvement du fluide, est relativement intense devant les forces de viscosité que le fluide va opposer pour se déplacer. On peut alors opposer cet écoulement au régime laminaire qui est régulier. Pour étudier le comportement complexe des écoulements turbulent, il faut, dans la plupart des cas, utiliser la voie statistique. En effet, on peut, de ce fait, considérer que cette étude fait partie intégrante de la physique statistique afin de traduire que, lors d'un écoulement, les forces d'inertie l'emportent sur les forces de viscosité.
Exercice : le tube de Pitot dans les avions
Le tube de Pitot est une sonde très simple mais essentielle à la sécurité de tous les avions puisqu'elle donne une mesure de la vitesse v de l'air par rapport à l'avion. Le schéma ci-dessus représente la partie de tube face à l'écoulement. Un manomètre différentiel permet la mesure de p(A)-p(B). On néglige la pesanteur.
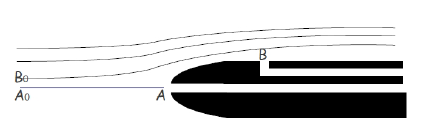
- Justifier que la vitesse de l'air au point B est peu différente de v.
- Justifier que la vitesse de l'air en A est nulle.
- En déduire alors le lien entre la différence de pression entre les points A et B et v.
- Calculer la différence de pression mesurée si v = 300 km/h. Commenter.
La plateforme qui connecte profs particuliers et élèves
Vous avez aimé cet article ? Notez-le !
Loading...
Si vous désirez une aide personnalisée, contactez dès maintenant l’un de nos professeurs !