Chapitres

Exercice 1 :
On considère deux plans parfaitement conducteurs P et P’ infinis, parallèles, distants de d et symétriques par rapport au plan 0yz. On étudie une onde électromagnétique progressive, monochromatique, se propageant dans le vide entre ces deux plans suivant la direction Oz (propagation guidée), et telle que son champ électrique reste parallèle aux deux plans. On posera donc E = E(x).ej(ωt-kz) y
1 - a) Ecrire l’équation de Maxwell-Faraday en notation complexe. En déduire la forme du champ Β en fonction de x, z, t. Est-il transversal ?
1 - b) Ecrire l’équation de Maxwel-Ampère et en déduire l’équation différentielle vérifié par E(x). S’assurer que les deux équations de Maxwell restantes sont bien vérifiées par E et B.
2 - Résoudre l’équation différentielle de 1-b). Montrer qu’on trouve plusieurs modes de propagation possibles et que chacun d’eux n’existe que si la pulsation de l’onde est supérieure à une valeur que l’on déterminera. Calculer dans chaque cas la vitesse de phase et la vitesse de groupe de l’onde.
3 - On ne considère plus, pour une pulsation donnée, que le mode dont le vecteur d’onde a le module le plus grand. Déterminer les valeurs moyennes du vecteur de Poynting et de la densité volumique d’énergie électromagnétique en un point situé entre P et P’. Calculer le flux énergétique moyen à travers une surface S perpendiculaire à Oz et de longueur h dans la direction 0y ; calculer l’énergie électromagnétique localisée en moyenne dans une tranche d’espace d’épaisseur dz et limitée par deux surfaces telles que S. En déduire la vitesse de propagation de l’énergie moyenne et la comparer à la vitesse de groupe.

Exercice 2 : Etude sur les ondes
Le texte ci-dessous est composé d'extraits d'un cours d'océanographie, que l'on peut découvrir sur le site web de l'IFREMER (édité par son laboratoire de physique des océans) : "Les ondes dans l'océan".
En océanographie, les ondes de surface se matérialisent par une déformation de l'interface entre l'océan et l'atmosphère. Les particules d'eau mises en mouvement au passage d'une onde se déplacent avec un petit mouvement qui leur est propre, mais restent en moyenne à la même position.
La houle est formée par le vent : c'est un phénomène périodique, se présentant sous l'aspect de vagues parallèles avec une longueur d'onde λ de l'ordre de 100 m au large, où la profondeur moyenne de l'océan est d'environ 4000 m.
On peut classer les ondes de surface, en fonction de leurs caractéristiques et de celles du milieu de propagation, en "ondes courtes" et en "ondes longues".
Ondes courtes : lorsque la longueur d'onde l est faible par rapport à la profondeur locale h de l'océan (au moins λ < 0,5.h).
Leur célérité v est définie par : \[v = \sqrt { \frac { g \cdot \lambda} { 2 \pi} }\]
Ondes longues : lorsque la longueur d'onde l est très grande par rapport à la profondeur h de l'océan (λ >10.h), les ondes sont appelées ondes longues.
Leur célérité v est définie par: v = \[v = \sqrt { g \cdot h }\]
(Note : g est l'intensité du champ de pesanteur terrestre ; on prendra g = 10 m.s–2).
I – Questions sur le texte
À propos de la houle.
1. Au large (avec h1 = 4000 m), la houle est-elle classée en ondes courtes ou longues ?
Évaluer la célérité v1 d'une houle de longueur d'onde λ1 = 80 m, ainsi que la période T de ses vagues.
2.En arrivant près d'une côte sablonneuse (profondeur d'eau h2 = 3,0 m), la longueur d'onde de la houle devient grande par rapport à la profondeur, elle rentre donc dans la catégorie des ondes longues. Sachant que sa période T ne varie pas, évaluer alors sa nouvelle célérité v2, ainsi que sa nouvelle longueur d'onde λ2.
3. Sur ces fonds (h2 = 3,0 m), les vagues de houle arrivent parallèlement à une digue rectiligne, coupée par un chenal de 30 m de large, et qui ferme une assez vaste baie.
Le vent local étant nul, que peut-on observer sur une vue aérienne de ce site, derrière la digue, coté terre ?
Dessiner l'aspect de la surface de l'eau (vagues), sur le document A (annexe à rendre avec la copie), de façon réaliste.
Quel nom porte le phénomène observé ? Avec quelles autres ondes (non mécaniques) peut-on observer le même phénomène ?
II – Au laboratoire du lycée, on veut compléter l'étude d'ondes analogues à la houle (en eaux peu profondes). On utilise une "cuve à ondes". Avec une webcam, on enregistre des vidéos de l'aspect de la surface de l'eau (en projection sur le verre dépoli vertical de la cuve). On traite ces vidéos à l'aide d'un logiciel adapté.
Dans un plan vertical, un vibreur anime d'un mouvement périodique (de période T), une réglette qui génère des vagues rectilignes parallèles, se propageant (sans réflexion) sur l'eau de la cuve, à la célérité v.
La profondeur h de l'eau est faible et constante. La webcam prend des images à des instants t, successifs séparés par Θ = 1 / 30 s = 0,033 s.
1. Selon la direction de propagation des ondes (axe xx'), on pointe sur des vues successives un même sommet de ride (ligne brillante sur le dépoli). On obtient, après étalonnage des distances, le tableau de mesures : document B en annexe.
a) Tracer sur le papier millimétré du document C (annexe à rendre avec la copie) le graphe x en fonction de t. En déduire la célérité v de cette onde. Est-elle constante ?
b) Sur l'une des vues du film, on pointe (selon xx') les sommets de la ride n°1 et de la ride n°4. La distance entre ces deux sommets est d = 0,088 m. D'autre part, une étude en lumière stroboscopique a permis de déterminer la fréquence f du vibreur: 8 Hz < f < 9 Hz.
- Évaluer la longueur d'onde λ de ces ondes.
- Les valeurs calculées de v et λ sont-elles en accord avec f donnée par le stroboscope ?
2. Les ondes émises par le vibreur sont transversales, pratiquement sinusoïdales. On néglige le phénomène de dispersion. A un instant t, une vue en coupe (dans un plan vertical) de la surface de l'eau présente l'aspect reproduit sur le document D (annexe à rendre avec la copie). (S est le point source, M est le front de l'onde).
a) Exprimer, en fonction de la période T des ondes, le retard t que présente le mouvement du point M, par rapport au mouvement de S (expression littérale demandée).
b) A l'instant suivant, le point M se déplace :
- Verticalement vers le haut ?
- Verticalement vers le bas ?
- Horizontalement vers la gauche ?
- Horizontalement vers la droite ?
Justifier votre réponse.
3. Sans rien modifier d'autre, on règle la fréquence du vibreur à f ' = 19 Hz. La mesure de la célérité des ondes donne alors : v ' = 0,263 m.s–1. Comparer cette célérité à celle trouvée au 1.a).
De quel phénomène, négligé jusqu'ici, la différence entre v et v ' est-elle la manifestation ? Ce phénomène est-il présenté par des ondes non mécaniques ? Lesquelles ? Citer une application.

Document B :
| t (s) | x (m) |
|---|---|
| 0,200 | 0,098 |
| 0,233 | 0,105 |
| 0,267 | 0,114 |
| 0,300 | 0,122 |
| 0,333 | 0,130 |
| 0,367 | 0,138 |
| 0,400 | 0,147 |



Exercice 3 : Le téléphone portable et les ondes radio
1. Les ondes électromagnétiques pour communiquer.
Le téléphone portable fonctionne comme une radio. Lors d’une communication, la voix est convertie en un signal électrique par un microphone. grâce à un système de conversion numérique et de modulation, ce signal électrique est couplé à une onde porteuse qui, après amplification, est émise vers l’antenne la plus proche. Celle-ci transmet le signal à une station de base qui l’envoie alors à une centrale, par ligne téléphonique conventionnelle ou par faisceaux hertziens. De là sont acheminées les conversations vers le téléphone du destinataire, selon le même processus, mais en sens inverse (non représenté sur le schéma). Après démodulation et conversion analogique, le signal électrique est transformé en signal sonore par le haut parleur de l’appareil récepteur.
Les ondes électromagnétiques sont déjà très largement utilisées pour la télévision, la radio, la C.B. et les radars, si bien que les gammes de fréquences restantes pour les portables sont de plus en plus restreintes. L’une d’entre elles s’étend de 890 à 915 MHz. Or, un appel nécessite une bande passante de 200 kHz. Autrement dit, dans cette bande de fréquence de largeurs 25 MHz, on ne devrait pourvoir passer que 125 appels simultanément.
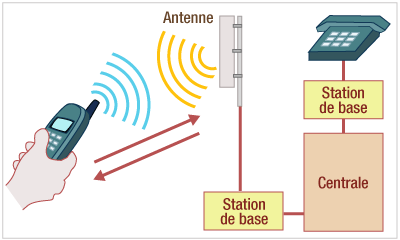
La solution a été le fractionnement du réseau en cellules (d’où le terme parfois utilisé de téléphone "cellulaire"). Le territoire français a donc été divisé en 40 000 parcelles, chacune comportant des antennes assurant la liaison avec les téléphones mobiles situés dans leur zone d’influence. Chaque parcelle possède ses propres fréquences, différentes de celles des parcelles voisines. Pas de risque d’interférence, donc…
1.1. Quel est l’ordre de grandeur de la fréquence des ondes porteuses utilisées pour le téléphone portable ?
1.2. En déduire l’ordre de grandeur de sa longueur d’onde dans le vide.
On donne la célérité de la lumière dans le vide c = 3 x
108 m.s-1
2. L’émission d’une onde électromagnétique par un portable.
On peut représenter symboliquement la chaîne d’émission par le schéma de la figure 1 :
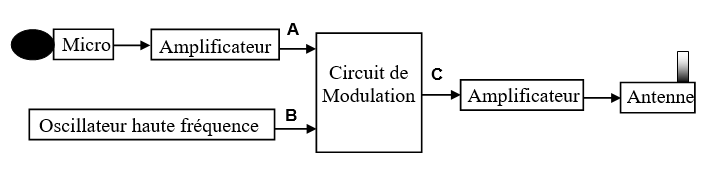
2.1. En quel point, A, B, ou C de la figure 1 trouve-t-on :
2.1.1. L’onde porteuse ?
2.1.2. Le signal modulant ?
2.2. L’onde porteuse est sinusoïdale et a pour expression v(t) = Vm cos (2π fp t). Le signal modulant est en général complexe, mais comme tout signal périodique, il peut se mettre sous la forme d’une somme de fonctions sinusoïdales.
Pour simplifier, nous prendrons pour le signal modulant, l’expression : u(t) = Um cos ( 2π fm t). On envisage une modulation d’amplitude, c’est à dire que le signal modulant va modifier l’amplitude de la porteuse.
2.2.1. Pour obtenir une modulation de bonne qualité, faut-il choisir fp très supérieure ou très inférieure à fm ?
2.2.2. Le circuit de modulation est constitué d’un composant nommé « multiplieur ». On branche respectivement, sur l’entrée E1 de ce circuit, le signal modulant u(t) additionné d’une tension de décalage U0, sur l’entrée E2, le signal de la porteuse v(t), et on recueille en sortie le signal modulé, nommé s(t).
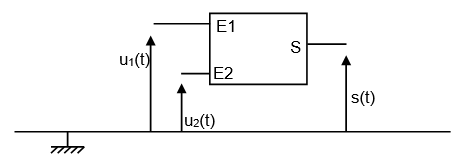
Avec u1(t) = u(t) + U0 et u2(t) = v(t)
Sachant que s(t) a pour expression générale s(t) = k.u1(t).u2(t), où k est une constante dépendant uniquement du circuit électronique, écrire s(t) sous la forme s(t) = Sm cos(2πfpt) et identifier Sm, l’amplitude du signal modulé.
2.2.3. En posant A = k.Vm.U0 et m = Um/U0, montrer que Sm peut se mettre sous la forme Sm = A (m.cos2πfmt + 1).
2.2.4. Quelle condition doit remplir m, le taux de modulation, pour que celle-ci soit de bonne qualité ?
2.3. Afin d’étudier le phénomène de modulation d’amplitude, on utilise un logiciel de simulation qui permet d’obtenir l’allure de la tension modulée s(t) en fonction du temps. Les valeurs numériques ont été choisies pour une lecture facile mais ne représentent pas l’onde réelle émise par un portable.

2.3.1. Déterminer la fréquence fp de la porteuse, utilisée pour la simulation.
2.3.2. Déterminer la fréquence fm du signal modulant, utilisé pour la simulation.
2.3.3. Déterminer Sm max et Sm min, les valeurs maximale et minimale de l’amplitude du signal modulé et en déduire le taux de modulation défini par : \[m = \frac {S_\text{m max} - S_\text{m min}} {S_\text{m max} + S_\text{m min}}\]
3. La réception d’une onde électromagnétique et sa démodulation.
On peut représenter symboliquement la chaîne de réception par le schéma de la figure 2 :

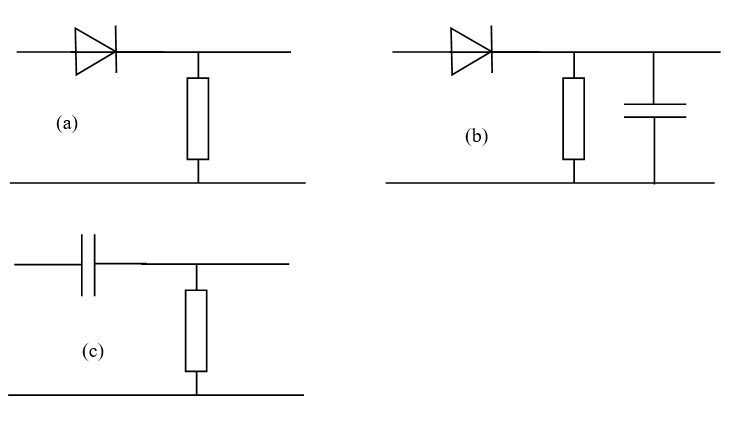
3. Parmi les circuits ci-dessous, indiquer celui qu’il convient d’utiliser :
3.1. pour le détecteur d’enveloppe.
3.2. pour le filtre passe-haut.

Exercice 4 : La télévision numérique et son fonctionnement
Ces dernières années, l’évolution des technologies a permis des progrès dans les systèmes de transmission de l’information. En 2005, la télévision numérique terrestre (TNT) apparaît et s’étend progressivement à tout le territoire. En 2011, la France abandonne totalement la télévision analogique.
La TNT a permis le développement de chaînes de télévision supplémentaires qui, en 2016, basculent entièrement en haute définition (TNT HD).
Certains téléviseurs disponibles actuellement commencent à préparer la prochaine étape avec la ultra haute définition et l’arrivée, d’ici 2025, de la TNT ultra HD.
Document 1 : La haute définition HD et l’ultra haute définition (ultra HD)
La HD, actuellement diffusée sur la TNT est une HD dite entrelacée, au format HD 1080i/25 : l’image est constituée de 1080 lignes de 1920 pixels chacune et le flux vidéo […] est équivalent à 25 images par seconde. La TNT classique a une résolution de 480 lignes de 720 pixels chacune.
Dans le HD dit progressif, aussi appelé HD 1080p/50, ce sont 50 images complètes par seconde qui sont transmises dans le flux vidéo. C’est ce format qui est utilisé sur les disques Blu-Ray par exemple. Selon les experts, ce format permet d’obtenir une meilleure qualité perçue de la vidéo, notamment pour les scènes rapides et le sport. La HD 1080p/50 pourrait devenir la norme à terme. En effet, certains estiment que la HD entrelacée 1080i/25 n’est qu’un format de transition en attendant la migration complète de la chaîne de production (captation, archivage, etc…) et de diffusion vers la HD 1080p/50. Toutefois, sa diffusion nécessite plus de débit. […]
D’après : CSA Rapport sur l’avenir de la plateforme TNT, Janvier 2013
Document 2 : Extrait d’une notice de câble coaxial pour relier une antenne à une télévision
Câble d’antenne TV 17VATC classe A :
- Câble coaxial de 100 m utilisable pour la réception TV ;
- Haut niveau de blindage qui le protège très efficacement contre
les parasites et interférences électromagnétiques ; - Atténuation a = 0,17 dB.m-1 pour une fréquence de 800 MHz lors du raccordement de l’antenne ou de la parabole au récepteur (télévision, démodulateur satellite).
1. Propagation des ondes radio
1.1. On considère la transmission d’une information par un signal de fréquence 800 MHz. Justifier le choix de cette fréquence.
1.2. On constate que la réception reste possible même si l’émetteur relais n’est pas visible pour un observateur situé au niveau de l’antenne réceptrice.
Expliquer comment cela est possible et justifier en faisant intervenir les dimensions des ouvertures des maisons.
1.3. Les chaînes de télévision émises par une antenne relais sont reçues en quasi-simultané par tous les récepteurs situés à moins de 50 km de cette antenne.
Vérifier cette affirmation en explicitant le raisonnement suivi.

2. Atténuation du signal
2.1. Attribuer chacun des deux schémas (a) et (b) ci-dessous à un signal analogique et à signal numérique. Justifier.
2.2. On considère qu’au-dessus d’une puissance de 20 nW (nanowatt) reçue par le téléviseur, l’image affichée peut être considérée comme satisfaisante. L’antenne est reliée au téléviseur par un câble coaxial 17VATC de classe A.
Déterminer à quelle distance maximale de l’antenne d’une maison, un téléviseur peut-il se trouver si l’antenne reçoit un signal de puissance de 100 nW à 800 MHz ?
3. Débit et transmission d’une chaîne HD
L’affichage d’une couleur, pour un pixel d’un écran, fait intervenir les trois couleurs primaires : codage RVB (Rouge, Vert, Bleu). On suppose que ce codage utilise 3 octets pour chacun des pixels. Par exemple, le codage d’un pixel rouge est (255, 0, 0).
3.1. Donner, en le justifiant, le codage d’un pixel noir et celui d’un pixel blanc.
3.2. Déterminer le débit nécessaire pour transmettre les images d’une chaîne de télévision haute définition HD 1080p/50 en bits par seconde puis en Gigabits par seconde.
3.3 Préciser quelle technique permet d’envoyer trois chaînes HD sur un canal de 24 Mbit.s-1 alors que ceci ne semble pas suffire pour une seule chaîne.






















Si vous désirez une aide personnalisée, contactez dès maintenant l’un de nos professeurs !