Chapitres

Exercice 1 : Freiner par induction
Un aimant de moment magnétique M est solidaire de la poulie de moment d’inertie J. Les deux petites spires S1 et S2 d’axes Ox et Oy sont identiques, ont même résistance R, et sont à la même distance du centre de la poulie.
Etudier l’évolution du système, l'ensemble étant immobile à t = 0.

Exercice 2 : L'alimentation des injecteurs automobiles
Dans les moteurs d’automobile moderne, le carburant est introduit à l’aide d’injecteurs.
L’ouverture et la fermeture de l’injecteur sont commandées par un électroaimant.
Dans cet exercice, on s’intéresse à la bobine (composant de l’électroaimant).
Le document ci-dessous représente l’évolution de la tension uL(t) aux bornes de l’électroaimant et la périodicité de l’injection lorsque le moteur fonctionne à « 3000 tours par minute ».


1. Étude de la tension aux bornes de la bobine
1.1 Déterminer la période T de la tension uL(t) à partir du document a.
1.2 La période T’ du cycle de l’injection vaut-elle : ∆t, ∆t’ ou ∆t + ∆t’ ?
1.3 Comparer T et T’.
1.4 Montrer que la valeur de T’ est en accord avec les « 3000 tours par minute » effectués par le moteur.
2. Détermination de l’inductance de la bobine de l’injecteur
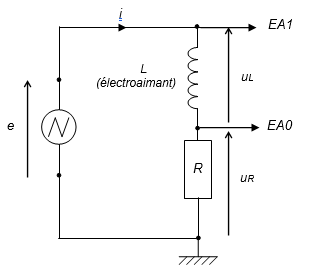
Pour déterminer l’inductance L de la bobine (supposée idéale) on réalise le circuit ci-après.
Le générateur utilisé délivre une tension e(t) triangulaire asymétrique. La résistance R vaut 1,00 kΩ.
Un système d’acquisition et son logiciel de traitement permettent d’obtenir les courbes suivantes :
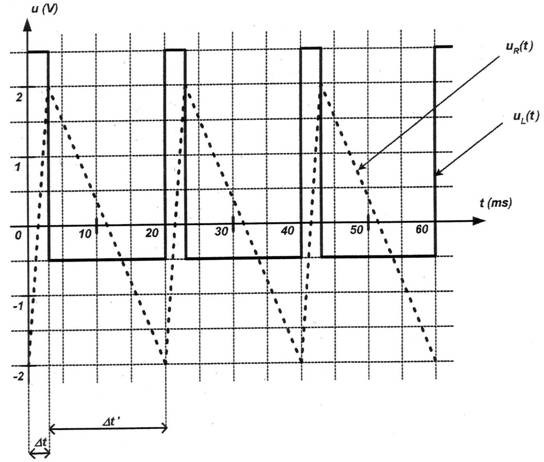
2.1. Visualisation des tensions
2.1.1 Quelle tension visualise-t-on sur l’entrée EA0 du système d’acquisition ?
2.1.2 Quelle tension visualise-t-on sur l’entrée EA1 du système d’acquisition ?
2.2. Comment a-t-on obtenu la courbe uL(t) à partir des tensions enregistrées en EA0 et EA1 ?
2.3. Exploitation des acquisitions
2.3.1. Donner l’expression littérale de uR(t) en fonction de i(t).
Exercice 3 : Etude de la Dacia Logan
La Dacia Logan, conçue par le constructeur français Renault est produite au départ en Roumanie.
Elle a fait la une de l'actualité lors de son lancement commercial : elle était en effet présentée
comme « la voiture à 5000 euros ». Même si son prix fut finalement plus élevé que prévu, les journalistes automobiles étaient impatients d'évaluer cette voiture d'un nouveau genre.
L'exercice propose de détailler certains tests routiers effectués par les essayeurs d'un magazine automobile et d'étudier un composant du système d'alimentation en gazole du moteur Diesel qui peut équiper la Logan.
Donnée : Accélération de la pesanteur: g = 9,8 m.s-2.

PARTIE A : Performances et comportement routier
I - Mesures de reprises
Le test consiste à faire passer la voiture, en pleine accélération et sur le deuxième rapport de la boîte de vitesses, de 30 km.h-1 à 70 km.h-1 sur une portion de circuit rectiligne et horizontale. On mesure alors le temps nécessaire à cette accélération, ce qui donne une bonne indication de la capacité du véhicule à s'insérer et à évoluer dans le trafic routier.
Résultat du test d'accélération donné par le magazine: «passage de 30 km.h-1 à 70 km.h-1 en 5,4 s ».
1. Le vecteur accélération est supposé constant pendant tout le mouvement ; sa norme est notée a1. Le schéma ci-dessous donne les différentes conventions utilisées. L'origine des temps est choisie à l'instant où le centre d'inertie G du véhicule passe au point O avec la vitesse v0 = 30 km.h-1.
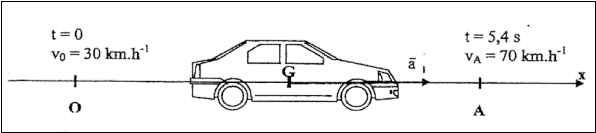
a) Donner la relation entre le vecteur accélération et le vecteur vitesse du centre d'inertie G du véhicule. En déduire l'équation horaire de la vitesse du centre d'inertie du véhicule v(t) en fonction de a1, v0 et t.
b) En utilisant le résultat du test d'accélération, montrer que la valeur de l'accélération a1 du véhicule en unité SI est : a1 = 2,1 m.s-2.
2. a) Établir l'équation horaire de la position x(t) du centre d'inertie G en fonction des grandeurs de l'énoncé.
b) En déduire la distance D parcourue par la Logan quand elle passe de 30 km.h-1 à 70 km.h-1, en 5,4 s.
II - Virage sur une trajectoire circulaire
Un second test consiste à faire décrire à la voiture une trajectoire circulaire de rayon R = 50 m. Ce test donne une bonne indication de la tenue de route du véhicule.
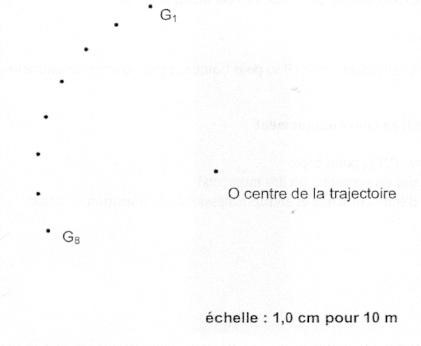
Une chronophotographie (en vue de dessus) représentant les positions successives du centre d'inertie G de la Logan pendant ce test est donnée en annexe à rendre avec la copie (Figure 1 ). La durée t = 1,00 s sépare deux positions successives du centre de masse G.
1. a) Exprimer les normes des vitesses v3 et v5 du centre d'inertie G aux points G3 et G5 en fonction des distances G2G4, G4G6 et de la durée t.
b) En utilisant la figure 1 montrer que ces vitesses v3 et v5 ont la même valeur d'environ
40 km.h-1.
c) Représenter les vecteurs vitesse 3 et 5 sur la figure 1 (échelle: 1 cm pour 2 m.s-1).
d) Représenter le vecteur D4 = 5 -3
2. a) Donner l'expression du vecteur accélération 4 au point G4, en fonction de D4 et t.
b) Calculer la valeur de a4 en unité SI.
3. a) Le constructeur qualifie cette accélération de « latérale ». Quel autre qualificatif utiliserait-on plutôt en physique ?
b) Peut-on considérer que, pour les passagers de la voiture, l'effet de cette accélération est négligeable devant celui de l'accélération de la pesanteur ?
III - Suspension
La Logan est constituée d'une caisse métallique reposant sur ses roues par l'intermédiaire d'une suspension, formée d'un ensemble de quatre ressorts avec amortisseurs. On peut modéliser cette voiture par un pendule élastique vertical dont les oscillations sont amorties. La seule particularité de ce pendule est d'avoir la masse M (correspondant à la caisse) à l'extrémité supérieure du ressort de raideur k ; la mise en oscillation ayant lieu lorsque l'extrémité inférieure du ressort (correspondant à la roue) subit un déplacement vertical, par exemple lors d'un passage sur une bosse (dos d'âne).

1. On considère la caisse de la Logan de masse M = 1 095 kg à l'arrêt, sans passager. Le ressort est alors comprimé. On appelle |∆ι0| la valeur absolue de la différence entre sa longueur à vide et sa longueur en charge.
a) Faire l'inventaire des forces qui s'exercent sur la caisse.
b) Trouver la relation entre |∆ι0|, M, k et g en appliquant le principe d'inertie.
2. Quatre essayeurs, de masse totale m = 280 kg, montent à bord de la Logan. La caisse s'affaisse d'une hauteur h = 3,0 x 10-2 m. La variation de la longueur du ressort en valeur absolue devient : |∆ι| = |∆ι0| + h.
a) Déterminer la dimension de k.
b) Calculer la valeur numérique de k.
3. On note T0 la période propre des oscillations de la caisse de la Logan avec un essayeur, de
masse m1 = 70 kg, sans passager. Montrer que T0 = 0,71 s.
4. Afin que le confort des passagers soit optimal lors du passage sur une bosse, les réglages de la suspension sont prévus pour que la caisse retrouve sa position initiale sans osciller.
a) L'essayeur prend le volant d'une Logan neuve et roule sur une bosse. Quel est le nom du régime oscillatoire observé ?
b) L'essayeur recommence l'expérience avec une Logan ayant déjà beaucoup roulé. Ses amortisseurs étant « fatigués », l'amortissement de la caisse est moins important. Prévoir
le comportement de la caisse dans ce cas en utilisant le vocabulaire adapté.
5. A nouveau au volant de la Logan neuve, l'essayeur, de masse m1 = 70 kg, aborde maintenant un ralentisseur installé par une municipalité à l'entrée de l'agglomération. Il est constitué d'une série de bosses distantes d'une longueur D. Le pendule élastique qui modélise la voiture est donc soumis à une succession d'excitations : la caisse subit des oscillations forcées.
L'essayeur constate que l'amplitude des oscillations est beaucoup plus importante qu'au passage d'une seule bosse, la voiture devient plus difficile à contrôler et le conducteur doit ralentir.
a) Quel nom donne-t-on au phénomène observé par l'essayeur ?
b) Quelle doit être la période des excitations pour que ce phénomène ait lieu ?
c) Cette période est la durée ∆t que met la voiture pour passer d'une bosse à l'autre. Calculer la distance D nécessaire pour que le phénomène ait lieu à une vitesse
v = 80 km.h-1.
d) Ainsi construit, ce ralentisseur devrait obliger les conducteurs trop rapides à ralentir pour respecter la vitesse de 50 km.h-1 en agglomération. Mais y aurait-il un autre moyen d'éviter le phénomène ressenti lors du passage sur le ralentisseur ? Si oui, expliquer.
(On ne tentera pas l'expérience !)
PARTIE B : « L'injecteur par rampe commune »
Malgré les tarifs modérés de la Logan, son moteur Diesel bénéficie d'une technologie de pointe: le système d'injection directe de gazole par rampe commune. L'élément essentiel est l'injecteur qui pulvérise en quelques fractions de seconde une très faible quantité de gazole directement dans la chambre de combustion où se produit l'explosion du mélange air-gazole.
On peut schématiser cet injecteur par un long tube creux, percé à son extrémité inférieure d'un très petit trou bouché par une aiguille. C'est par ce trou que pourra sortir le gazole lorsque l'aiguille sera déplacée vers le haut.
Pour déplacer cette aiguille métallique vers le haut, on utilise une bobine qui, lorsqu'elle est traversée par un courant électrique, se comporte comme un aimant et attire alors l'aiguille à elle. Dès que le courant est coupé, l'aiguille reprend sa position initiale et bouche à nouveau le trou.
Un laboratoire de recherche d'un constructeur concurrent demande à un technicien d'étudier les caractéristiques de cette bobine.
I - Prévision d'un dipôle bobine-conducteur ohmique
Pour préparer un protocole d'étude de la bobine de l'injecteur, le technicien choisit d'abord une bobine, d'inductance L et de résistance interne r connues.
Il réalise ensuite le circuit ci-contre où l'interrupteur est au départ fermé.
On rappelle que la tension aux bornes de la bobine est : [ u_{L} = L \cdot \frac { text {d} i } { text {d} t } + r \cdot i ]
Données :
- E = 6,0 V; L = 0,94 H ;
- R0 =150 W; r = 20 W.
1. L'interrupteur K étant fermé, et le régime permanent établi, l'intensité dans le circuit est constante et notée I0.
Montrer que : [ I _ {0} = \frac { E } { R _ {0} + r }]
2. A l'instant t0 = 0, l'interrupteur est ouvert. On a alors la relation uL(t) + uR0 (t) = 0. Établir l'équation différentielle vérifiée par l'intensité i(t).
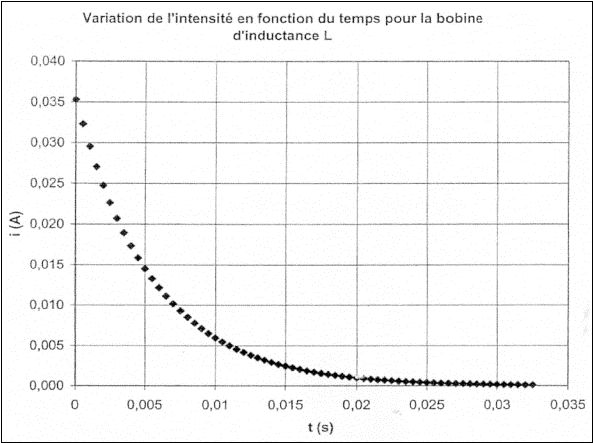
3. Le technicien utilise une interface d'acquisition et un capteur de tension pour suivre l'évolution temporelle de la tension uR0 (t), à l'ouverture de l'interrupteur. Un tableur permet alors de calculer le graphe de l'intensité du courant et de tracer le graphe de son évolution temporelle donnée sur la figure 2 de l'annexe.
a) A partir de l'allure de la courbe i(t) de la figure 2, préciser le rôle de la bobine dans ce circuit.
On note [ tau = \frac { L } { R _ { 0 } + r }] la constante de temps de ce circuit.
b) Montrer que τ a la dimension d'un temps.
c) Calculer τ.
d) Mesurer sur le graphique l'intensité i(τ) pour t = τ.
II - Mesure des caractéristiques de la bobine de l'injecteur
Le technicien utilise maintenant la bobine de l'injecteur afin de déterminer son inductance L' et sa résistance r' .
Il réalise avec cette bobine le circuit de l'étude précédente (E = 6,0 V; R0= 150 Ω) et il effectue une nouvelle acquisition comme à la question I-3.
A l'instant t0 = 0, il ouvre l'interrupteur et obtient le tracé donné sur la Figure 3 en annexe à rendre avec la copie.
A l'aide de l'étude précédente et du graphique de la figure 3, déterminer :
1. La résistance interne r' de la bobine.
a) Évaluer graphiquement la constante de temps t'.
b) Déterminer l'inductance L' de la bobine.
Annexes

Exercice 4 : Un record en TGV
Le dernier record du monde de vitesse sur rail du TGV (Train à Grande Vitesse) a été homologué le 3 avril 2007. Une rame expérimentale a atteint à 13h14 la vitesse de 574,8 km·h−1 sur la toute nouvelle ligne Est européenne.
L’alimentation des moteurs électriques du TGV est réalisée à l’aide de la caténaire et du pantographe.

La caténaire est le câble électrique tendu au-dessus des voies. Le pantographe est le dispositif articulé fixé sur le toit de la locomotive, permettant une liaison électrique par frottement sur la caténaire.
Le pantographe appuie sur le câble et le soulève, créant une déformation en forme de V inversé. Lorsque le train se déplace, une onde mécanique progressive se propage dans la caténaire devant la locomotive. Si le train rattrape l’onde, le contact entre le pantographe et la caténaire est rompu et la puissance électrique transmise aux moteurs diminue. La célérité de l’onde dans la caténaire est une contrainte qui limite la vitesse du train, on parle d’un « mur de la caténaire » par analogie avec le mur du son.
1. L’onde qui se propage dans la caténaire est progressive et mécanique. Rappeler la définition d’une onde progressive puis indiquer ce qui permet de la qualifier de mécanique.
Un système de poulies et de contrepoids permet de tendre plus ou moins la caténaire. Pour étudier l’influence de cette tension mécanique T (en Newton), on utilise un logiciel de simulation mis en ligne par l’université du Colorado. Dans cette simulation la caténaire du train est modélisée par la corde sur laquelle se propage une perturbation. Deux captures d’écran de ce logiciel sont données ci-dessous.


2. Déterminer, à l’aide des deux captures ci-dessus la valeur de la vitesse de propagation de l’onde dans la simulation.
3. Une deuxième simulation avec une valeur de tension plus élevée du câble donne une célérité de 6,3×10-2 m·s-1. Indiquer l’influence du paramètre tension sur la célérité de l’onde.
L’expression littérale de la célérité de l’onde mécanique qui se propage dans la caténaire est :
[c = \sqrt { \frac { T } { rho \cdot S } }]
Avec :
- c la célérité de l’onde en mètres par seconde (m·s-1) ;
- T la tension exercée sur la caténaire en Newton (N) ;
- S la section de la caténaire (m2) ;
- ρ la masse volumique du matériau constitutif du câble (kg·m−3).
La SNCF a spécifié que pour des trajets commerciaux, la vitesse de ses TGV ne devait pas dépasser 70 % de la vitesse de propagation des ondes dans la caténaire.
Nous disposons des informations suivantes sur les caténaires utilisées :
| Tension T (N) | 2,6×104 |
|---|---|
| Section S (mm2) | 150 |
| Masse volumique ρ du cuivre (kg·m−3) | 8920 |
4. Vérifier la cohérence de cette relation avec les résultats obtenus lors de la simulation.
5. Déterminer, en m·s−1 puis en km·h1, la valeur de la vitesse théorique maximale que ne doit pas dépasser un TGV en exploitation commerciale.
6. Proposer une argumentation d’une dizaine de lignes en indiquant sur quels paramètres les ingénieurs ont pu agir pour repousser le mur de la caténaire et ainsi faire franchir au TGV la barre symbolique des 500 km·h−1.
On précisera dans le raisonnement les paramètres modifiés, le sens d’évolution de leurs valeurs (plus élevée ou plus faible) ainsi que le choix le plus approprié et le plus économique.
Freinage d’urgence et distance de freinage
Un TGV commercial de masse M = 425 t roulant à la vitesse v0 = 320 km·h−1 sur une voie que l’on supposera rectiligne et horizontale doit effectuer un arrêt d’urgence. La valeur de la distance nécessaire pour que le TGV s’immobilise (distance d’arrêt) est de 3,2 km.
Au cours d’un essai dans la phase de préparation du record, un incident a déclenché le freinage d’urgence et la rame expérimentale (de masse M’ = 270 t roulant à la vitesse v1 = 501,6 km·h−1) s’est immobilisée au bout de 15 km.
7. À l’aide d’une approche énergétique, justifier le sens de l’évolution de cette distance d’arrêt.
Alimentation électrique des moteurs
Pour fournir plus de puissance aux moteurs électriques de la rame, la tension électrique de la caténaire a été portée à 31 kV contre 25 kV en temps normal. Lors des essais, la valeur de l’intensité du courant traversant le pantographe est en moyenne égale à 800 A.
8. Calculer la valeur de la puissance électrique fournie par la caténaire aux moteurs électriques.
La puissance restituée par l’ensemble des moteurs a été estimée à 19 600 kW (soit plus du double de celle d’une rame de TGV classique).
9. Recopier et compléter le schéma suivant qui représente le bilan de puissance des moteurs de la rame.

10. Exprimer et calculer le rendement de l’ensemble des moteurs de la rame expérimentale. Expliquer pourquoi il ne peut être supérieur à 1.
Résumer avec l'IA :






















Si vous désirez une aide personnalisée, contactez dès maintenant l’un de nos professeurs !