Chapitres
Pendant votre cursus scientifique de seconde, vous énoncerez de nombreux thèmes et sujets. Afin de préparer au mieux votre entrée en Première, vous devrez maîtriser certains chapitres. Nous allons dans cet article les revoir et aussi vous proposer quelques exercices pour apprendre à maîtriser ces notions.

Domaines sur lesquels travailler
Les interactions fondamentales
Savoir appliquer la loi du Coulomb
Les lois de Coulomb sont deux lois physiques qui s'appliquent à deux domaines différents.
L'une est applicable à l'électrostatique et l'autre est adaptable à la mécanique.
Loi de Coulomb en électrostatique
La loi de Coulomb est une loi énoncée par le physicien d'origine française Charles-Augustin Coulomb en 1785. Elle est l'expression de la force qui s'exerce entre deux particules chargées électriquement.
Voici son énoncé :
L'intensité de la force électrostatique entre deux charges électriques est proportionnelle au produit des deux charges et est inversement proportionnelle au carré de la distance entre les deux charges. La force est portée par la droite passant par les deux charges
Cette loi a été énoncée sur la base de mesures que Coulomb avait réalisé grâce à sa balance de Coulomb. Cette balance permet de mesurer l'axe de torsion entre deux particules chargées. En fonction de l'angle à l’équilibre, on peut donc en déduire la force exercée sur chacune des deux particules.
Voici l'expression de la force de Coulomb exercée par une charge électrique :
[overrightarrow { F } _ { \frac { 1 } { 2 } } = \frac { q _ { 1 } q _ { 2 } }{ 4 pi epsilon _ { 0 } } \cdot \frac { overrightarrow { r } _ { 2 } - overrightarrow { r } _ { 1 } } { | | overrightarrow { r } _ { 2 } - overrightarrow { r } _ { 1 } | | ^ { 3 } }]
Avec :
- F force exercée par une charge électrique ;
- q1 charge électrique placée au point r1 ;
- q2 charge électrique placée au point r2.
A connaître : la constante universelle diélectrique, également connue sous le nom de permittivité du vide : ε0 = 8,854 x 10-12.
Il ne faut pas oublier non plus que la loi de Coulomb est applicable uniquement dans le cadre des charges fixes et pas en mouvement.
Loi de Coulomb en mécanique

En mécanique cette fois, la loi de Coulomb est une loi qui exprime les intensités des forces exercées entre deux solides.
En cours de physique chimie, cette loi introduit donc les deux notions de frottements suivantes : l'adhérence et le glissement. Derrière adhérence se cache une idée de frottement statique et derrière la notion de glissement se cache une idée de frottement dynamique.
Le glissement ne se produit qu'après dépassement de la composante tangentielle T0.
On calcule la force limite T0 à l'aide de la loi de Coulomb :
[ T _ { 0 } = f _ { 0 } times N ]
Avec :
- f0 coefficient d'adhérence ou de frottement statique dont la valeur dépend des matériaux et des surfaces en frottement.
Retrouvez ici tous nos cours physique chimie 3ème pour progresser.
Forces macroscopiques
Savoir identifier et représenter des actions qui s'exercent sur un solide
Différentes forces s’exercent sur les solides. Vous devrez savoir les décrire.
Le poids
Le poids d'un objet est représenté par la force qui s'exerce sur celui-ci et l'attirant vers le sol. Sur la Terre, dans le référentiel terrestre, il s'agit de la gravité.
Le poids se calcule avec la formule suivante :
[ P = m \cdot overrightarrow { g } ]
Avec :
- P, poids en Newtons : N ;
- m, masse de l'objet en kilogrammes : kg ;
- g, vecteur de la pesanteur terrestre : 9,81 N / kg.
La réaction du support
Lorsqu'un objet se déplace, la réaction de frottement avec son support doit être prise en compte.
En effet, la surface de contact crée de l'adhérence et des forces de frottement.
Poussée d'Archimède
La poussée d'Archimède est une force découverte par le physicien Archimède. Elle est la force subie par un corps plongé dans un fluide liquide ou gazeux et soumis à un champ de gravité.
Par exemple, c'est la poussée d'Archimède qui fait qu'on flotte dans sa baignoire, mais aussi qu'une montgolfière vole.

On définit donc le vecteur poussée d'Archimède :
[ P _ { A } = µ times V times g ]
Avec :
- PA en Newtons : N ;
- µ masse volumique du fluide en kilogrammes par mètre cube : kg / m3 ;
- V volume en mètres cubes : m3 ;
- g intensité de la pesanteur à la surface de la Terre en Newtons par kilogramme : N / kg et de valeur 9,81.
Une approche des lois de Newton
Savoir appliquer les lois de Newton
Les lois de Newton se comptent au nombre de 3. Elles ont été énoncées par Newton, un physicien britannique ayant vécu entre 1642 et 1727.
Première loi de Newton
Corpus omne perseverare in statu suo quiescendi vel movendi uniformiter in directum, nisi quatenus a viribus impressis cogitur statum illum mutare
Si un corps ne subit pas de force, alors sa vitesse est constante. Soit le corps est au repos et a une vitesse nulle ou soit il se déplace en ligne droite avec une vitesse constante et non nulle.
Deuxième loi de Newton
Mutationem motus proportionalem esse vi motrici impressae, et fieri secundum lineam rectam qua vis illa imprimitur
Le vecteur accélération d'un corps est parallèle et directement proportionnel à la force appliquée sur le corps. Ce vecteur est dans la même direction que la force.
Troisième loi de Newton
Actioni contrariam semper et æqualem esse reactionem: sive corporum duorum actiones in se mutuo semper esse æquales et in partes contrarias dirigi
Lorsqu'un premier corps exerce une force sur un deuxième corps, le deuxième corps exerce simultanément une force opposée sur le premier. Ainsi les deux forces exercées par les corps l'un sur l'autre sont égales et opposées en direction.
Travail d'une force
Savoir exprimer et calculer le travail d'une force constante
On appelle travail d’une force constante F, lors d’un déplacement rectiligne de son point d’application de A vers B, le produit scalaire de la force F par le vecteur déplacement AB :
[ W _ { A B } ( overrightarrow { F } ) = overrightarrow { F } \cdot overrightarrow { A B } = F \cdot A B \cdot text {cos}(overrightarrow { F } ; overrightarrow { A B } ) ]
Avec :
- WAB (F) en joules : J ;
- F en Newtons : N ;
- AB en mètres : m.
Travail et énergie cinétique
Savoir utiliser l'expression de l'énergie cinétique et l'appliquer entre deux instants
Définition
L'énergie cinétique est l'énergie que possède un corps grâce à son mouvement. Exprimée en joules, elle se calcule avec l'expression suivante :
[ E _ { c } = \frac { 1 } { 2 } m \cdot v ^ { 2 } ]
Travail et énergie potentielle de pesanteur
Savoir expliciter la transformation d'énergie potentielle en énergie cinétique
Si toutes les forces extérieures appliquées à un solide, à l'exception du poids, effectuent un travail nul, la somme de l'énergie cinétique et de l'énergie potentielle de pesanteur est constante, conservant ainsi l’énergie mécanique.
Voici l'expression qui lie énergie cinétique à l'énergie potentielle de pesanteur.
Ec(B) - Ec(A) = WAB( P ) = m . g . (zA - zB) = m . g . zA – m . g . zB = Epp(A) – Epp(B) = Ec(A) + Epp(A) = Ec(B) + Epp(B)
Travail et énergie interne : transfert thermique

Savoir que l'énergie reçue par travail peut aussi être « stockée » par un corps
Un transfert thermique a lieu lorsque deux corps de températures différentes entrent en contact. Le transfert s'effectue du corps le plus chaud vers le corps le plus froid. Il a lieu jusqu'à ce que les deux corps soient à la même température.
Soit la relation suivante :
[ Delta U = U _ { f } - U _ { i } = m c ( theta _ { f } - theta _ { i } ]
Avec :
- U énergie d'un corps pur ;
- m masse du corps pur ;
- c capacité thermique massique ;
- θi température initiale ;
- θf température finale.
Générateurs et récepteurs en courant continu
Utiliser le principe de la conservation de l'énergie pour faire un bilan d'énergie
Réaliser le bilan énergétique d'une ressource consiste à établir le rapport entre la quantité d'énergie dépensée pour extraire la ressource et celle finalement disponible à l'exploitation.
Si le bilan énergétique est négatif, il faut fournir plus d'énergie pour extraire la ressource que la ressource n'en fournira par elle même.
Exercice 1 : Bille chinoise
La Tour Nina à Hong Kong est un des plus hauts gratte-ciel du monde. Elle comprend 102 étages et culmine à 468m. Une bille d'acier est abandonnée sans vitesse initiale du haut de cette immeuble. On suppose que les forces de frottement dues à l'air sont négligeables.

1. Quelle force s'exerce sur la bille pendant la chute ?
2. Quel est son mouvement si elle part sans vitesse initiale ?
3. En utilisant la formule liant la vitesse V et la durée T de la chute ( V = G T ), calculer au bout de quel temps la vitesse de la bille atteint 13,9 m/s ? 100 km/h ?4. En utilisant la formule liant la hauteur H et la durée T de la chute (H = 0,5 G T² ), calculer le temps que met la bille pour parcourir les 100 premiers mètres ? Les 100 mètres suivants ?
Exercice 2 : Les lois de Newton
Un objet de masse m = 3,80 x 10–3 kg, de volume V = 2,10 x 10–6 m3 est lâché sans vitesse initiale dans un liquide de masse volumique r = 1240 kg.m–3. Sa chute est filmée avec une webcam. Le film est ensuite numérisé puis analysé par un logiciel adapté.
Le document fourni en annexe, montre l’ensemble des positions successives occupées par le centre d’inertie G de l’objet à intervalles de temps réguliers t = 0,050 s.
Les frottements du fluide sur l’objet peuvent être modélisés par une force f opposée au vecteur vitesse et de valeur proportionnelle à la vitesse ; le coefficient de proportionnalité appelé coefficient de frottement sera noté k.
On prendra g = 9,8 m.s-2.
1. Le document fourni en annexe, montre que le mouvement de chute comporte deux phases de nature différente.
Délimiter les deux phases en précisant approximativement les positions limites de chacune d’elles.
2. Étude de la première phase
2.1. À partir du document :
2.1.1. En tenant compte de l’échelle du document, calculer les vitesses en positions G3 et G5 puis tracer sur le document de l’annexe à rendre avec la copie, les vecteurs vitesse en ces positions en utilisant l’échelle 1 cm pour 0,20 m.s-1.
2.1.2. Calculer l’accélération a4 au point G4 puis tracer sur le document de l’annexe à rendre avec la copie, le vecteur accélération en ce point avec l’échelle 1 cm pour 0,50 m.s-2.
2.2. Étude théorique
2.2.1. Calculer la valeur de la poussée d’Archimède et montrer qu’elle est de l’ordre de grandeur du poids.
2.2.2. Représenter les forces sur un schéma sans souci d’échelle.
2.3. Énoncer la loi de Newton qui régit cette première phase.
2.4. En utilisant l’axe Oz dessiné sur la figure ci-dessus, calculer la valeur de la force de frottements en position G4.
2.5. Sachant que la vitesse en position G4 vaut v4 = 0,32 m.s-1, calculer la valeur du coefficient de frottement k en unité du système international.
3. Étude de la deuxième phase
3.1. Quelle est la nature de cette phase ?
3.2. Énoncer la loi de Newton qui régit cette phase.
3.3. Déterminer, par le calcul, la vitesse de l’objet au cours de cette phase.
3.4. Retrouver cette vitesse à partir du document en utilisant le point G13.
Annexe à rendre

Exercice 3 : Mesurer la profondeur de l'eau
La connaissance du relief du fond des eaux est indispensable dans des domaines variés : géologie, navigation, pêche, activité pétrolière, pose de câbles sous-marins, etc. Cet exercice s’intéresse à trois méthodes employées pour cartographier le fond des océans.
1. Sondage à main
Le sondage à main est réalisé par un marin sur un bateau. Un lest* est attaché à l’extrémité d’une corde graduée ; il est ensuite jeté par-dessus bord. La mesure de la profondeur de l’eau est obtenue en estimant la longueur de la corde lorsque le marin sent que le lest touche le fond de l’eau.
* lest : objet massif servant à alourdir un système.
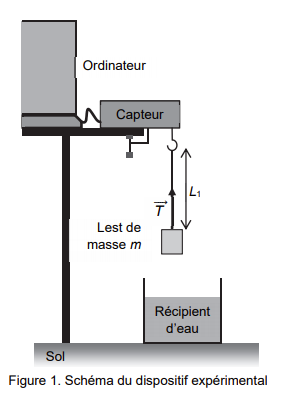
Pour illustrer le principe du sondage à main, une expérience, schématisée sur la figure 1, est réalisée au laboratoire.
Un lest de masse m = 100 g est attaché à une corde peu extensible de longueur L1 et de masse négligeable. Un capteur mesure la valeur de la tension T ሬሬሬԦ qu’exerce la corde sur le lest. Lorsque la corde n’est pas tendue, la tension est nulle. Une série de mesures avec des cordes de plus en plus longues est réalisée. Pour une longueur donnée, la mesure est effectuée quand le lest est immobile. Pour les premières mesures, le lest est hors de l’eau. L’étude est conduite dans le référentiel du laboratoire, supposé galiléen. Les actions exercées par l’air sont négligées.
Les résultats de l’expérience complète (lest en dehors de l’eau puis dans l’eau) sont reproduits sur la figure 2 ci-après. Les coordonnées de quelques points (longueur de la corde en cm ; tension de la corde en mN) sont données entre parenthèses.

Données :
- Intensité du champ de pesanteur terrestre : g = 9,81 m·s–2 ;
- Tout corps immergé dans un fluide subit de la part du fluide une action modélisée par une force FA verticale, dirigée vers le haut et appelée poussée d’Archimède.
- L’expression de sa norme est donnée par la relation : FA = ρfluide × Vimmergé × g où Vimmergé est le volume de la partie du corps immergé et ρfluide est la masse volumique du fluide ;
- Masse du lest : m = 100 g ;
- Masse volumique de l’eau : ρeau = 1,00 × 103 kg·m3 ;
- Masse volumique du plomb : ρplomb = 1,14 × 104 kg·m-3.
1.1. Étude du système en dehors de l’eau
On considère la situation de la figure 1 dans laquelle le lest n’est pas encore plongé dans l’eau, la corde est tendue.
1.1.1. Effectuer le bilan des forces extérieures qui s’exercent sur le lest.
1.1.2. À l’aide d’une des lois de Newton, déterminer la valeur de la norme de la tension de la corde. Indiquer si la valeur mesurée par le capteur lors de cette première mesure est cohérente avec ce résultat.
1.1.3. Exploiter les résultats expérimentaux de la figure 2 pour estimer la valeur de la longueur de la corde pour laquelle le lest touche la surface de l’eau.
1.2. Étude du système dans l’eau
On étudie désormais la situation pour laquelle le lest est intégralement placé sous la surface de l’eau sans reposer sur le fond.
1.2.1. Indiquer à quelle nouvelle force le lest est maintenant soumis.
1.2.2. Exploiter les résultats expérimentaux de la figure 2 pour déterminer la valeur de cette nouvelle force.
Déterminer la valeur du volume du lest et en déduire si le lest est entièrement constitué de plomb ou non. Le candidat est invité à prendre des initiatives et à présenter la démarche suivie même si elle n'a pas abouti. La démarche suivie est évaluée et nécessite donc d'être correctement présentée.
1.2.3. Quelle est la situation représentée par le point P présent sur la figure 2 ? Justifier.
1.2.4. Estimer la valeur de la profondeur h de l’eau.
2. Sondage avec un sonar
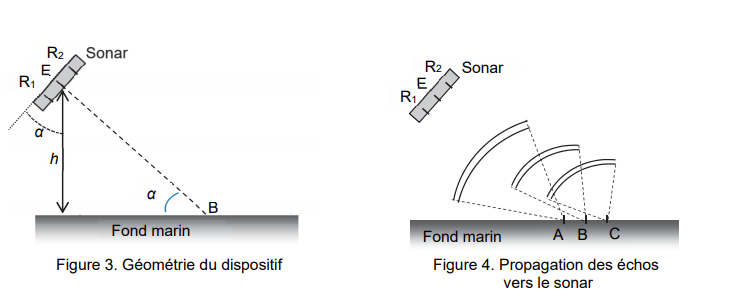
Pour sonder le fond marin, on utilise un sonar composé d’un émetteur à ultrasons E, situé à égale distance de deux récepteurs R1 et R2. Ce sonar est incliné d’un angle α par rapport à la verticale (voir figure 3). L’émetteur émet des salves ultrasonores qui se propagent vers le fond marin qui les renvoie dans toutes les
directions. Les récepteurs R1 et R2 du sonar reçoivent les signaux issus du fond marin. Les ondes ultrasonores diffusées par les points A, B et C sont reçues par les récepteurs R1 et R2 à des dates différentes. On cherche à comprendre comment le sonar distingue les signaux issus du point B, qui est à égale distance des récepteurs R1 et R2, des signaux issus d’autres positions du fond marin (voir figure 4).
Donnée :
- Valeur supposée constante de la célérité des ondes ultrasonores dans l’eau : v = 1,53 km·s-1.
On représente ci-dessous, sans aucun souci d’échelle, la simulation des signaux reçus au cours du temps par les récepteurs R1 et R2.
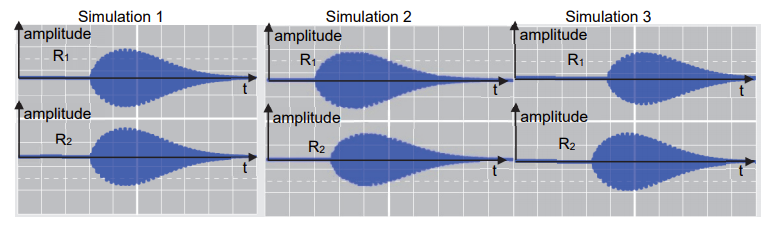
2.1. Associer une simulation à chacun des points A, B et C du fond marin. Justifier.
Le sonar mesure avec précision la valeur de la durée qui sépare l’émission des ultrasons et la réception des échos issus du point B : ΔtS = 27,7 ms. Le sonar est incliné par rapport à la verticale de l’angle α = 30°.
2.2. En déduire la valeur de la profondeur h du fond de l’eau sous le sonar. Les distances EB, R1B et R2B sont considérées comme étant égales.
3. Sondage avec LIDAR (LIght Detection And Ranging)
Un LIDAR est un appareil qui fonctionne sur le même principe que les sonars en employant des ondes électromagnétiques. Une brève onde électromagnétique est émise par le LIDAR en direction d’un obstacle et l’appareil mesure la durée Δt au bout de laquelle l’écho lui revient. Un LIDAR est placé dans un avion qui survole une zone à étudier, il émet des signaux électromagnétiques,
une partie de ces signaux est réfléchie par la surface de l’eau, une autre partie est réfléchie par le fond marin. La valeur de la célérité c, dans le vide, des ondes électromagnétiques est supposée connue des candidats.
3.1. Étude des ondes électromagnétiques employées
Le LIDAR est équipé d’un LASER qui émet des ondes électromagnétiques dont la longueur d’onde dans le vide est λ = 1,064 µm.
3.1.1. Dans quel domaine du spectre électromagnétique ces ondes sont-elles situées ? Justifier
Tous les rayonnements ne se propagent pas de manière équivalente dans l’eau. L’« absorption par cm d’eau » d’une onde électromagnétique indique la proportion de l’intensité lumineuse absorbée par centimètre parcouru dans l’eau par l’onde électromagnétique (figure 5).
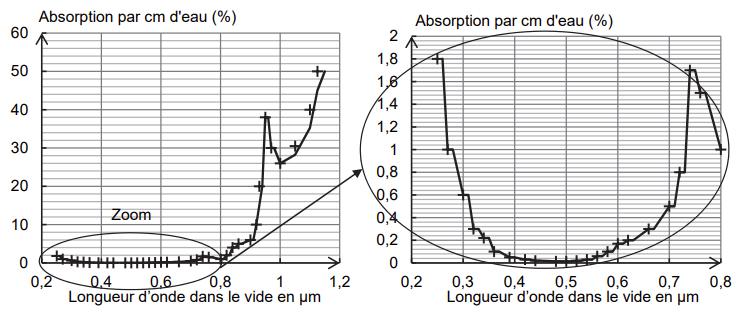
3.1.2. Déterminer si le rayonnement électromagnétique produit par le LASER est approprié pour détecter
le fond marin. Justifier.
3.1.3. Des dispositifs permettent soit de doubler soit de tripler la fréquence des ondes électromagnétiques.
Déterminer s’il est plus approprié de doubler ou de tripler la fréquence du rayonnement émis par le LASER pour détecter le fond marin. Justifier.
3.2. Exploitation des données recueillies par le LIDAR
Pour le domaine de longueur d’onde utilisé par le LIDAR, la célérité d’une onde électromagnétique dans l’eau à une température de 20 °C vaut 2,26×108 m·s–1. Au cours d’un vol au-dessus de l’eau, le capteur LIDAR placé dans l’avion émet un signal dont il capte deux échos après des durées Δt1 = 2,67 µs et Δt2 = 3,04 µs.
Déterminer les valeurs de la hauteur de vol de l’avion au-dessus de l’eau et de la profondeur de l’eau survolée.




















Si vous désirez une aide personnalisée, contactez dès maintenant l’un de nos professeurs !