Chapitres

Présentation de l'appareil
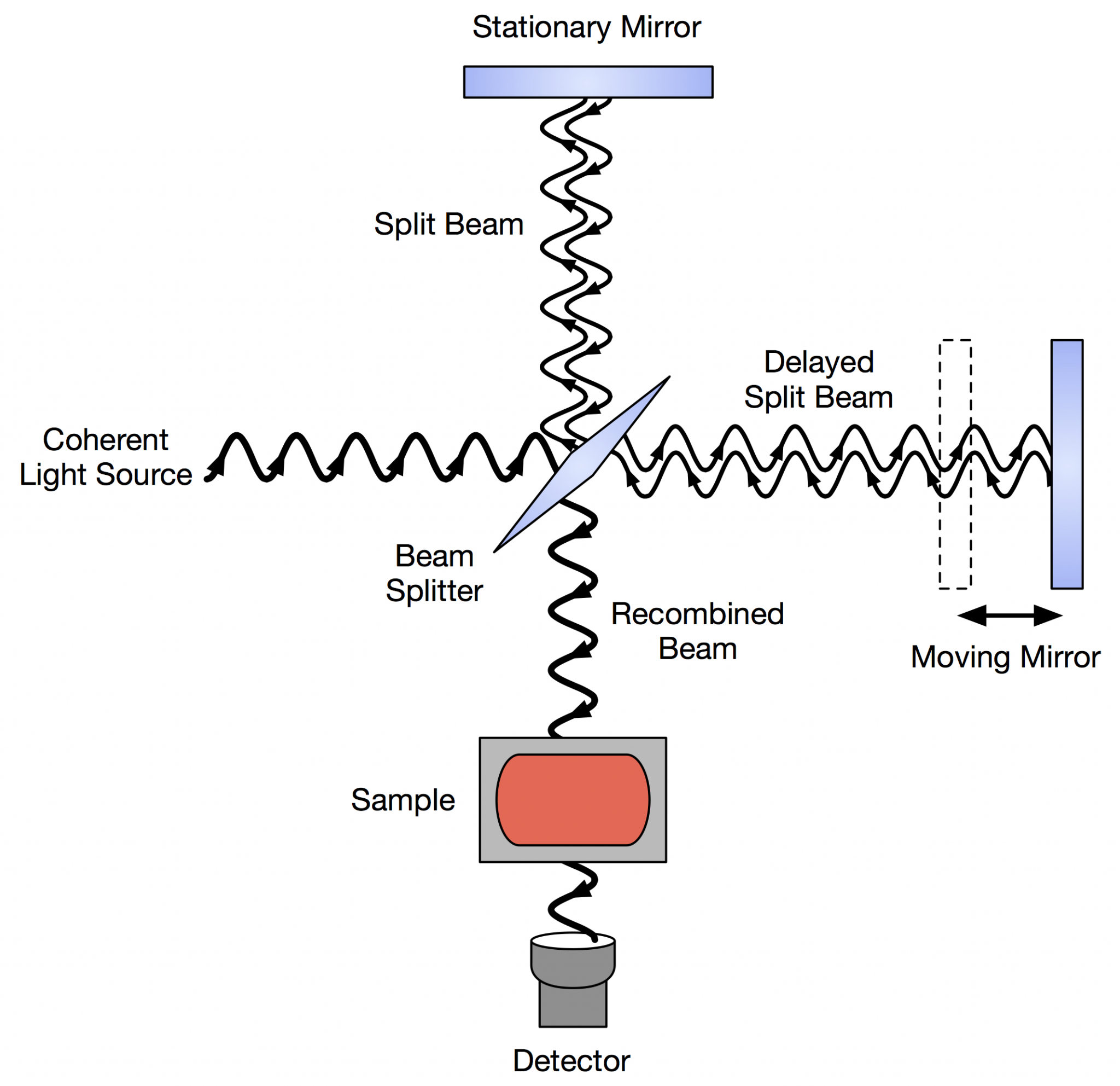
L'interféromètre de Michelson est un dispositif optique d'interférences qui les produit par division d'amplitude. Il a été mis au point par deux physiciens américains : Albert Abraham Michelson et Edward Morley.
Albert Abraham Michelson
Albert Abraham Michelson est un physicien américain ayant vécu entre 1852 et 1931.
Tout au long de sa carrière, il a travaillé sur la détermination de la vitesse de la lumière. A cette époque où l'on croyait encore que l'univers était plongé dans l'éther et que c'était la seule possibilité pour que la lumière se propage, Michelson a beaucoup travaillé sur les interférences, ce qui l'a conduit à inventer son interféromètre.
Michelson reçut de nombreux prix et distinctions tels que :
- Prix Rumford en 1888 ;
- Médaille Matteucci en 1903 ;
- Médaille Copley en 1907 ;
- Médaille Henry Draper en 1916.
Il a été récompensé en 1907 par le prix Nobel de physique pour des travaux en optique, métrologie et spectrographie.
Edward Morley
Edward Morley est lui aussi un physicien américain qui vécut entre 1838 et 1923. Avant de se rendre connu pour son expérience menée avec Michelson, il était professeur de chimie.
Conjointement à ses recherches sur les interférences, il a travaillé sur la vitesse de la lumière, les champs magnétiques, la dilatation thermique mais aussi la composition gazeuse de l'atmosphère.
Tout comme son homologue Michelson, Morley a reçu plusieurs distinctions :
- 1907 : médaille Davy ;
- Willard Gibbs Award en 1912.
L'expérience de l'interféromètre
L'expérience menée par Michelson et Morley avait pour but de montrer l'existence de l'éther luminifère.
Il ont alors cherché à mettre en évidence la différence de vitesse de la lumière entre deux directions perpendiculaires et à deux périodes espacées de 6 mois.
Ils réalisèrent ces expériences entre 1881 et 1887.
L'expérience a été développée par Michelson et Morley dans le but de mesurer la vitesse de la lumière dans son support supposé, l'éther à l'époque, en se basant sur la loi d'addition des vitesses.
Il est apparu que la Terre sur son orbite avec une vitesse d'environ 30 km/s par rapport au Soleil était le laboratoire idéal pour déceler une variation de la vitesse de la lumière sur des parcours identiques en longueur mais qui devaient être différents en temps selon qu'ils seraient dans le sens du mouvement ou perpendiculairement au vent d'éther.
Ether luminifère
L'éther est défini en physique par des des substances distinctes de la matière et permettant de fournir ou de transmettre des effets entre les corps. Selon différents physiciens, l'éther était responsable de la gravitation, de la trajectoire des planètes ou encore du transport de la lumière.
L’éther luminifère est considéré comme l'éther responsable du passage de la lumière. De nombreux physiciens ont travaillé à la recherche de sa découverte jusqu'à ce que les expériences de Michelson et Morley réfutèrent cette théorie sans le vouloir.
Les interférences
- Soit un point de l'espace où parviennent deux ondes lumineuses sinusoïdales :
- Les vibrations s'ajoutent (principe de superposition du champ électrique) ;
- Les intensités ne s'ajoutent pas à priori.
- Si les intensités de chaque onde s'ajoutent en tout point de l'espace où les ondes se superposent, on dit qu'il n’y a pas interférences ;
- Il y a interférences dans le cas contraire : on observe des variations d'intensité dans l'espace ;
- II faut que les pulsations soient identiques pour qu'il y ait interférences. Cette condition est suffisante pour des ondes rigoureusement sinusoïdales (sinusoïdes illimitées dans le temps).
Expression de l’ordre d’interférences
-
Utilisation de la modélisation en lame d’air d’épaisseur e.
-
Les deux rayons qui interfèrent à l’infini sont issus d'un même rayon incident.
-
δ(M) = 2e.cos(i) et p(M)= (2e.cos(i))/λ.
-
p ne dépend pas de la position du point source de la source étendue mais uniquement de i : les figures d’interférences dues aux différents points source sont identiques. Les intensités s’ajoutant, la figure d’interférence est plus lumineuse. Cela justifie l’existence de franges visibles à l’infini.
Franges d’égale inclinaison
-
p ne dépend que de i donc les lignes équi-p sur l’écran sont des cercles (anneaux) de centre F’, foyer principal image de la lentille : franges d’égale inclinaison.
-
Champ d’interférences : limité par la valeur maximum de i.
Condition d’éclairage : faire l’image de la source sur le miroir M2 à l’aide d’un condenseur pour élargir le champ d’interférences.
-
Position des franges brillantes : “interfrange” non constant, franges de plus en plus resserrées quand on s’écarte du centre, rayon des anneaux.
-
Profil d'intensité : sinusoïdal car interférences à deux ondes.
-
Influence de la translation du miroir mobile : les anneaux rentrent au centre quand on diminue l'épaisseur e de la lame d'air (bon à savoir pour les travaux pratiques !)
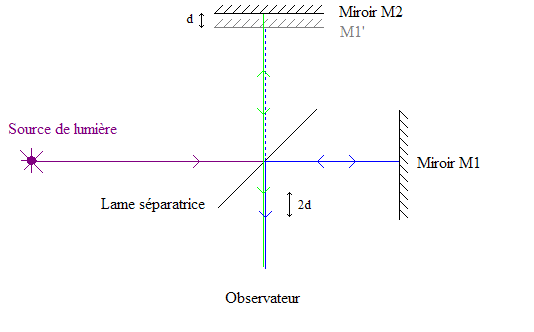
Les deux types d'interféromètres de Michelson
Interféromètre de Michelson équivalent à une lame d'air à faces parallèles
Pour une source ponctuelle, le calcul de la différence de marche en un point de l'espace à l’infini ne dépend pas de la position de la source. La figure d'interférence ne dépend donc pas de la position de la source. Elle sera donc identique pour une source large, mais plus lumineuse.
On admet que la figure d'interférence ne subsiste qu'à l'infini pour une source large : on dit que les interférences sont localisées à l'infini.
Interféromètre de Michelson équivalent à un coin d'air
Localisation des franges et conditions d’observation
-
Condition d’éclairage : l’interféromètre réglé en coin d’air est éclairé par une source spatialement étendue, sous incidence quasi-normale.
ADMIS : Les interférences sont dans ces conditions localisées au voisinage des miroirs.
-
En pratique,
-
on observe la figure d’interférences dans le plan conjugué du miroir M1 par une lentille convergente. On peut aussi les observer à l’oeil nu !
-
on éclaire l’interféromètre avec un collimateur : trou source dans le plan focal d’une lentille convergente.
-
Expression de l’ordre d’interférences
-
Utilisation de la modélisation en coin d’air d’angle α.
-
ADMIS : δ(M) ≈ 2e(M)
-
p(M) = 2e(M)/λ.
Franges d’égale épaisseur
-
p ne dépend que de e donc les lignes équi-p sur l’écran (conjugué à M1 par la lentille de projection) sont des segments parallèles : franges d’égale épaisseur.
-
Position des franges brillantes, interfrange i = λ/2α
-
Profil d'intensité : sinusoïdal car interférences à deux ondes.
-
Influence de l’angle du coin d’air : les franges sont d'autant plus resserrées que l'angle du coin d'air est grand (bon à savoir pour les travaux pratiques !)
Notion de cohérence spatiale
- Une source rigoureusement ponctuelle serait parfaitement cohérente spatialement ;
- Les exemples précédents montrent que l'on peut tout de même obtenir des interférences avec une source non ponctuelle : la source est dite spatialement cohérente.
Un autres type d’interférences : les interférence d'Young

On appelle fentes, ou interférences, de Young toute expérience consistant à faire interférer deux faisceaux de lumière qui sont issus d'une même source. Cette interférence est produite grâce au passage de la lumière dans deux petits trous qui auront été percé au sein d'un plan opaque. On observe alors pour résultat, sur un écran disposé face à ces fentes, un motif de diffraction représenté par une zone où des franges sombres et des franges illuminées sont disposées en alternance. Cette expérience permet ainsi de mettre en lumière la nature ondulatoire des ondes électromagnétiques. Lorsque cette même expérience est réalisée avec de la matière, comme des atomes, des molécules ou des électrons, il est possible d'observer ce même comportement. On peut ainsi observer la dualité onde-particule puisque les interférences permettent de montrer que la matière présente également un comportement ondulatoire bien que les impacts sur l'écran démontrent un comportement particulaire.
Trous d’Young éclairés par une source monochromatique non ponctuelle
- Pour une source fente infiniment fine, perpendiculaire à l'axe des sources : chaque point source donne la même figure d'interférence. La figure d'interférence est donc la même que pour une source ponctuelle, mais plus lumineuse.
- Pour une source fente large, perpendiculaire à l’axe des sources : lorsqu'on passe d'une fente source fine à une fente source fine voisine, la figure d'interférence se translate car un déphasage est introduit entre les deux sources secondaires.
- Sans calculs :
- Le contraste va varier en fonction de la largeur de la fente source.
- Détermination de la largeur de fente qui annule le contraste.
- Calcul complet du contraste en fonction de la largeur de fente.
Dispositif sans lentilles
- Description du dispositif : la source ponctuelle principale est constituée d'une lampe spectrale (plus filtre) et d'un petit diaphragme circulaire. Les sources secondaires sont créées grâce au phénomène de diffraction (voir plus loin).
- Détermination de la forme des franges : elles sont bien rectilignes. La différence de marche en tout point de l'écran ne dépend en effet que d'une seule variable.
- Détermination de l’interfrange : elle est égale au produit de la longueur d'onde par la distance de l'écran aux sources, divisé par la distance entre les deux sources. i=λD/a
- La position de la frange brillante d'ordre 0 est évidente pour un dispositif parfaitement symétrique.
- Si on admet que les franges sont rectilignes, on peut faire un calcul rapide pour retrouver l'interfrange et la position des franges.
Dispositif avec lentilles
- Description du dispositif : une lentille sert à éclairer les trous par une onde plane, une autre lentille sert à observer les interférences à l'infini.
- La présence de lentilles interdit le calcul de la différence de marche de façon purement géométrique car on ne connait pas les distances exactes parcourues dans la lentille.
Exemple de TP
Interféromètre de Michelson en coin d'air
On règle un interféromètre de Michelson en coin d’air.

On l’éclaire avec une lampe au mercure devant laquelle on a placé un diaphragme circulaire largement ouvert puis un filtre vert pour isoler sa raie verte de longueur d’onde 546,1 nm.
1. Doit-on ajouter une lentille devant la source ?
2. Les franges observées sont-elles localisées ? Si oui, où ?
3. Quelle est leur forme ?
4. Peut-on définir un interfrange ?
5. En utilisant une lentille de projection de distance focale 20 cm, on doit placer l’écran à 1,30 m de la lentille pour observer des franges nettes d’interfrange 4,0 mm. En déduire l’angle entre les miroirs.























Si vous désirez une aide personnalisée, contactez dès maintenant l’un de nos professeurs !