Chapitres

Rappel sur la propagation des ondes

Une onde se propage dans un milieu qui le lui permet car la propagation résulte de la mise en mouvement d’une particule dans le temps mais aussi dans l’espace par rapport au milieu. Cela est possible uniquement si la source est dans un état vibratoire.
On peut caractériser la propagation d’une onde par sa vitesse de propagation à l’aide la formule suivante : [ c = lambda times f ] Avec :
- c la célérité de l’onde ;
- λ la longueur d’onde ;
- f la fréquence de l’onde.
Remarque : La vitesse de la lumière est de 300 000 km.s-1 et la célérité d’une onde sonore est de 344 m.s-1
Rappel sur la réfraction des rayons lumineux
La réfraction est le changement de direction que subit un rayon lumineux lorsqu'il traverse la surface de séparation entre deux milieux transparents.
L'indice d'un milieu

Un milieu transparent est caractérisé par son indice de réfraction. L'indice de réfraction d'un milieu transparent correspond au rapport entre la célérité d'une onde se propageant dans le vide et sa célérité dans le milieu considéré. [ n = \frac { c } { v } ] Avec
- n correspondant à l'indice de réfraction du milieu transparent et qui est une grandeur sans unité ;
- c correspondant à la célérité de l'onde dans le vide. La célérité est égale à 3.108 m.s-1 ;
- Et v correspondant à la célérité de l'onde dans le milieu transparent qui s'exprime en m.s-1.
Un milieu est dit dispersif si la célérité d'une onde lumineuse monochromatique qui se propage dans ce milieu dépend de sa fréquence (donc de sa longueur d'onde dans le vide). L'indice de réfraction d'un milieu dispersif dépend donc de la fréquence de l'onde qui s'y propage.
La loi de Descartes
Cette loi lie les indices de réfraction (n1 et n2), l'angle d'incidence (i1) et l'angle de réfraction (i2). Elle s'exprime par la relation suivante : [ n _ { 1 } times sin left( i _ { 1 } right) = n _ { 2 } times sin left( i _ { 2 } right) ]
Définition : La réfraction de la lumière correspond au changement de direction du rayon lumineux lorsque celui-ci traverse une surface séparant deux milieux d'indices de réfraction différents.
En effet, la loi de Snell-Descartes de la réfraction exprime le changement de direction d'un faisceau lumineux lors de la traversée d'une paroi qui sépare deux milieux différents. Il faut d'abord savoir que chaque milieu est caractérisé par sa capacité à « ralentir » la lumière. On modélise cette caractéristique par son indice de réfraction n qui s'exprime sous la forme : [ n = \frac { c } { v } ] Où v est la vitesse de la lumière dans ce milieu et c est la vitesse de la lumière dans le vide (souvent arrondie à 3.108 m.s-1 Il est important de savoir que :
- Le rayon lumineux est dit incident avant d'avoir rencontré la surface réfractante (appelée dioptre), il est dit réfracté après avoir rencontré cette dernière.
- Le point de rencontre du rayon incident et du dioptre est appelé point d'incidence.
- Le plan contenant le rayon incident et la normale au dioptre, au point d'incidence est dit plan d'incidence.
- L'angle orienté i1 pris entre la normale au point d'incidence et le rayon incident est dit angle d'incidence.
- L'angle orienté i2 pris entre la normale au point d'incidence et le rayon réfracté est dit angle de réfraction.
- Les angles i1 et i2 sont positifs s’ils sont orientés dans le sens trigonométrique (sens inverse des aiguilles d'une montre), négatifs sinon.
On prend n1 l'indice de réfraction du milieu dans lequel se propage le rayon incident et n2 celui du milieu dans lequel se propage le rayon réfracté. Pour pouvoir énoncer la loi de la réfraction, il faut que le rayon réfracté, le rayon incident et la normale (au dioptre) soient dans un même plan qui est appelé le plan d'incidence et que le rayon incident et le rayon réfracté soient situés de part et d'autre de la normale. Lorsque n1 > n2 (et respectivement n1 < n2) le rayon réfracté (et respectivement : incident) se rapproche plus rapidement du dioptre que le rayon incident (ou réfracté). Cependant, il existe un cas particulier où le rayon réfracté (ou incident) se retrouve mathématiquement sur le dioptre (sa limite) : il y a alors réflexion totale.
Exemple de cas réel : la réfraction atmosphérique
La réfraction atmosphérique correspond à la déviation des faisceaux lumineux par des superposition de couchers d'air ayant des températures différentes. On se trouve alors dans le cas d'une propagation anormale de la lumière au sein d'une atmosphère dans laquelle la température, la pression ainsi que l'humidité restent constante verticalement selon la normale. Ainsi, la déviation des rayons lumineux peuvent donner l'impression que l'objet observé se situe autre que sa localisation réelle. De ce fait, il serait incorrect de définir un mirage comme une illusion d'optique ou encore comme une hallucination : il est possible de photographier un mirage ! En effet, il s'agit plutôt d'une déformation mentale d'une image provoquée par une interprétation fausse du cerveau.
Correction du problème 1

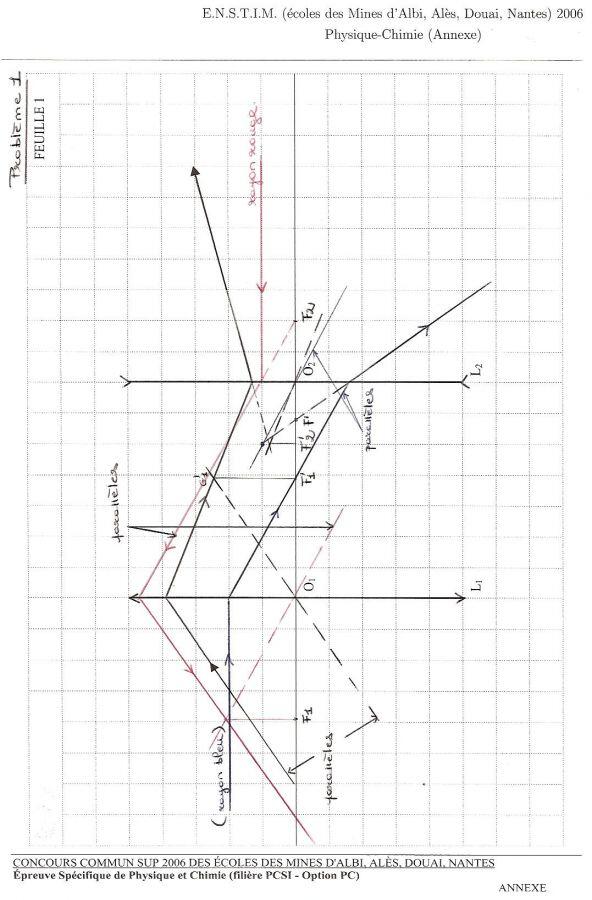
Partie 1
- Ce système est globalement convergent car le rayon émergent tracé fait avec l'axe optique un angle plus faible que le rayon incident correspondant.
- On prolonge les rayons émergent et incident jusqu'aux lentilles puis on trace le segment rectiligne qui relie les deux points d'impact.
- L1 est convergente car le rayon incident est dévié vers l'axe par L1, L2 est divergente car le rayon intermédiaire s'écarte de l'axe après la traversée de L2.
- Traçons le rayon incident parallèle au rayon incident du schéma et passant par 01. Les deux rayons sortant de Ll issus de ces incidents (objet B à l'infini hors de l'axe) se coupent en un foyer secondaire image G'1, image de B par LI. G'l est contenu dans le plan focal image et donc F'1 se trouve sur l'axe à la verticale de G’1. F1 est symétrique de F'1 par rapport à L1. On utilise la même méthode pour trouver
les foyers de L2.
On mesure sur le schéma : 01F'1 = 3,9 cm et O2F'2 = -2,0 cm - Le foyer objet F est le point de l'axe dont l'image est située à l'infini sur l'axe; le foyer image F' est
l'image d'un point à l'infini sur l'axe.Pour trouver graphiquement la position de F', on considère un rayon incident parallèle à l'axe, après passage par L1, il passe par F'i. On détermine l'image de F'l par L2 en considérant le rayon parallèle au rayon précédent et passant par 02 donc non dévié par L2. Ces deux rayons issus d'un objet à l'infini se coupent en l'image de cet objet, dans le plan focal image de L2. Pour le foyer objet, point objet donc l'image se trouve à l'infini sur l'axe, on utilise la même construction en imaginant que le rayon incident vient de la droite de la figure et est parallèle à l'axe.
O1F' = 5,8 cm (obtenu grâce au rayon bleu)
O1F = -7,1 cm (obtenu grâce au rayon rouge) - F' est conjugué de F'1 par L2 donc 1/O2F' - 1/O2F'1 = 1/12
d'où 1/O2F' = 1/02F'1 + 1/f2 = 1/(O2O1 + O1F 1) + 1/82 =- 5/6 cm-1
On en déduit O2F=- 1,2 cm c'est à dire 01F'= 5,8 cm
F est conjugué de F2 par L1 donc 1/O1F2 - 1/O1F=1/f'
d'où 1/O1F = 1/O1F2 - 1/f1 = 1/(O1O2 + O2F2) - 1/f"1 = -5/36 cm-1
On en déduit O1F=- 7,2 cm
On retrouve donc par le calcul des valeurs très proches de celles mesurées sur le schéma.
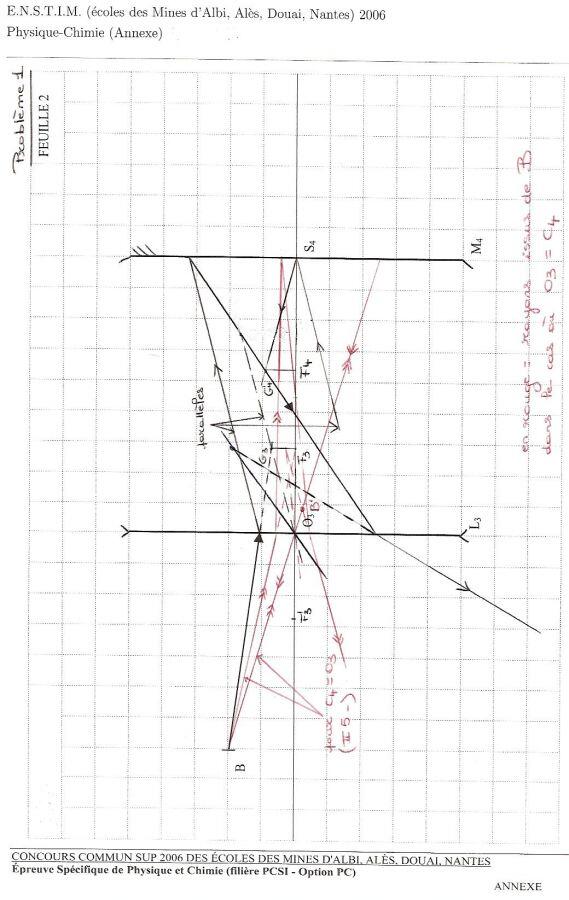
Partie 2
- Voir la figure 2.
- Traçons le rayon parallèle au rayon réel entre la lentille et le miroir avant réflexion et qui passe par O3. Les rayons incidents correspondants se coupent en un foyer secondaire G3. A sa verticale sur l'axe se trouve F3. F'3 est symétrique de F3 par rapport à O3.
Traçons à présent le rayon parallèle au rayon réel entre la lentille et le miroir avant réflexion et qui passe
par S4. Il se réfléchit sur M4 symétriquement à l'axe et coupe l'autre rayon en un foyer secondaire image
G'4. A sa verticale se trouve F4. On mesure O3F'3 = 2,8 cm S4F4 = -3,6 cm. - Pour tracer le rayon émergent du système, on utilise le rayon passant par 03 donc non dévié par L3 et parallèle au rayon réfléchi. Les deux rayons sortant de L3 se coupent en un foyer secondaire image donc dans le plan de F3 car la lentille est utilisée dans le sens droite/gauche.
Ce système est globalement divergent puisque le rayon sortant fait un angle plus important que l'incident
avec l'axe. - La lentille L3 divergente puisque f3>0
Le miroir M4 est convergent : un rayon parallèle à l'axe est réfléchi en étant rabattu vers l'axe. - Si le point C4 est confondu avec le point 03, le point B' image finale de B se trouve sur le rayon issu de B et passant par O3 : il n'est pas dévié par L3 puis se réfléchit sur lui-même et enfin traverse L3 dans l'autre sens sans être dévié. L'autre rayon de construction choisi est celui issu de B et passant par F3. Il ressort de L3 parallèle à l'axe et donc passe par F4 (attention : placé au milieu de O3S4) après réflexion sur M4. On construit alors le rayon final en utilisant un incident parallèle et un foyer secondaire image, donc ici dans le plan de F3.
A l'intersection des deux rayons qui ressortent du système et qui étaient issus de B se trouve B'.
Correction du problème 2
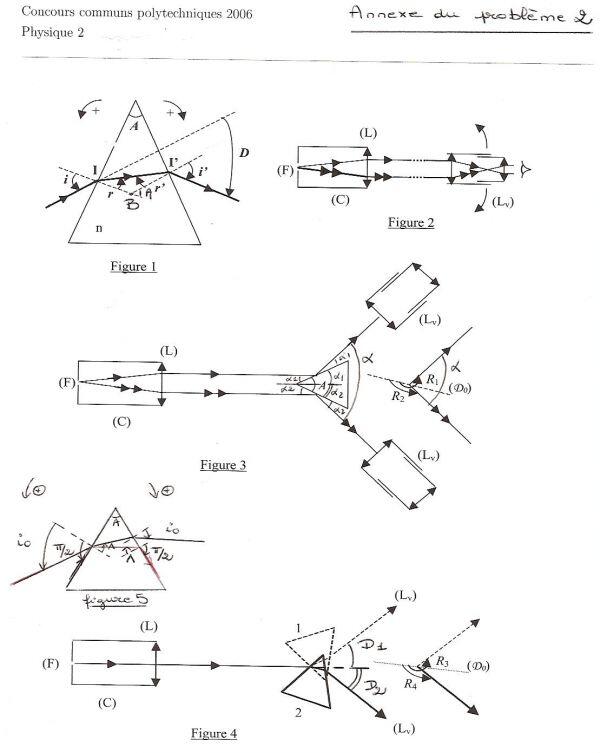
Formules du prisme
- Loi de Descartes de la réfraction : sin i = nsin r et sin i' = nsin r'
- En utilisant la somme des angles dans le triangle I l' B, on obtient A=r+r' (figure 1)
D = D1 + D2 = (i - r)+ (i - r')=i+i'-A
(avec D1 et D2 les déviations du rayon lumineux à la traversée des 2 dioptres plans qu'il rencontre)
Conditions d'émergence
- Au passage du deuxième dioptre, le rayon pénètre dans un milieu moins réfringent donc la réfraction
n'est possible que si r'est inférieur ou égal à A.
De plus r max = A (valeur obtenue lorsque i = i max = 90°)
Donc r +r'<24
On en déduit que k1 = 2 - r'max = A donc r min = A-r'max=A-A
Or sin i=n sin r donc i min = arc sin (n sin(A - A)
D'où i est bien supérieur ou égal à l'angle io défini dans l'énoncé, avec k2=n. - Si i=io, sin (io)=n sin (A - A ) donc sin r=A-A, r'= A et i'= 1/2
En utilisant le principe du retour inverse de la lumière et la symétrie du prisme, on peut dire que si
i=1/2, i' = 10. (schéma de la figure 5)
Minimum de déviation
- i=i' et r=r' puisque le rayon est symétrique par rapport au plan bissecteur de A.
- r=r' = A/2 et i= 1° = (A+Dm)/2 donc sin((A+Dm)/2) = sin(A/2)
- Il est astucieux ici d'utiliser la différentielle logarithmique car n se met sous la forme d'un quotient.
In(n) = In(sin((A+Dm)/2)) - In(sin(A/2))
d'ou en différenciant dn/n = cotan((A+Dm)/2) (d((A+Dm)/2)) - cotan(A/2) dA/2
c'est à dire dn/n = (JA/2) cotan((A+Dm)/2) - cotan(A/2)] + (dDm/2) cotan((A+Dm)/2)]
(ne pas oublier de rassembler les termes en dA avant de calculer les incertitudes)
An'n = (AA/2)| cotan((A+Dm)/2) - cotan(A/2) + (ADm 2) cotan((A+Dm)/2)
(ne pas oublier les valeurs absolues)
Mesure de l'indice n
- Voir le schéma de la figure 3 pour la définition des angles.
Ces angles vérifient A= α1 + α2, a - 2 x (α1 + α2) et α- R1 - R2 d'où R1 - R2 = 2A
R1-R2 = 119°52' d'où A = 59°56' ( 1° = 60 ) - ΔA = 1/2 (ΔR1 + ΔR2)
L'incertitude sur chaque mesure Ri vaut 2 x 1/30° soit 4' d'angle. Donc ΔA = 4'. - On tourne le prisme jusqu'à ce que le rayon sortant change de sens de rotation donc "Rebrousse
chemin" - Sur la figure 4, il apparaît que D1+D2=R3 - R4. Bien-sûr, D1 = D2 = Dm
donc 2Dm=R3 R4 = 97°-44' et Dm = 48°52' - (A+Dm) = 54°24' = 54,4° et A/2 = 29°58' = 29,9667° dc n= 1,62784...
Tant que la calcul d'incertitude sur n n'est pas effectué, il faut garder un grand nombre de chiffres
significatifs! - 0 < cotan ( ( A + Dm ) / 2 ) < cotan ( A / 2 )
d'ou Δn/n = (ε/2) - cotan(A+Dm)/2) + cotan(A/2)) + (ε/2 )cotan((A+Dm)2)
An/n = (ε/2) cotan(A/2). On vérifie la formule donnée dans l'énoncé avec k3 = 1/2. - Attention : dans ce calcul, e doit être exprimé en radian: π rad = 180° = 180/60' = 3'
Δn/n = 1,009.10-3 d'où Δn = 1,6452.10-3 = 2.10-3
Attention : on arrondit une incertitude ! - n= 1,628±0,002
Remarque : on n'est pas trop étonné de trouver une incertitude relative très faible sur n (0,1%) car la
mesure demande un appareillage assez lourd et de précision donc coûteux.
Annexes
Résumer avec l'IA :






















Si vous désirez une aide personnalisée, contactez dès maintenant l’un de nos professeurs !