Chapitres

Exercice 1 : Répondez aux questions
1- La vitesse de la lumière est C=3,00x108 m.s-1 dans le vide.
2-Une année lumière, noté a.l, est la distance parcourue par la lumière en 1an dans le vide.
3- Cette unité nous permet de mesurer une distance à l'échelle astronomique. Elle nous permet de mesurer une distance très grande.
4-La lumière ne se propage pas instantanément. Par exemple si nous observons une étoile a 8 a.l de nous, cela veut dire que nous voyons cette étoile comme elle était il y a 8 ans, car la lumière a mis 8 ans avant d'atteindre l'étoile.
Exercice 2 : Ecriture scientifique

Tableau à compléter
| Longueurs | Conversion (en m) | Ecriture scientifique (en m) | Ordre de grandeur (en m) |
|---|---|---|---|
| 12760 km | 1,276 x 107 m | 107 m | |
| 0,78 µm | 0,78 x 10-6 m | 10-6 m | |
| 543 nm | 543 x 10-9 m | 5,43 x 10-7 m | 10-6 m |
| 0,0345 x 10-3 m | 3,45 x 10-5 m | ||
| 87625 cm | 1 |
Correction
| Longueurs | Conversion (en m) | Ecriture scientifique (en m) | Ordre de grandeur (en m) |
|---|---|---|---|
| 12760 km | 127 x 103 m | 1,276 x 107 m | 107 m |
| 0,78 µm | 0,78 x 10-6 m | 7,8 x 10-7 m | 10-6 m |
| 543 nm | 543 x 10-9 m | 5,43 x 10-7 m | 10-6 m |
| 0,0345 mm | 0,0345 x 10-3 m | 3,45 x 10-5 m | 10-5 m |
| 87625 cm | 87625 x 10-2 m | 8,7625 x 102 m | 103 m |
Exercice 3 : Répondez aux questions
La nébuleuse de l’Hélice est une nébuleuse planétaire située dans la constellation du Verseau. Elle est située à environ d=6,58x1015 km de notre système solaire et son diamètre D mesure 2,9 al.
a) Conversion en a.l:
1al= 9,47x1015 m=9,47x1012
d=6,58x1015 /9,47x1012 =694,8 a.l
694,8=6,948x102 al.
La nébuleuse de l'Hélice se situe à 6,948x102 a.l.
b) L'ordre de grandeur de 6,58x1015 km est d=1016 km
L'ordre de grandeur de 6,948x102 a.l est d=103 a.l
c) La lumière met 694,8 ans environs pour nous parvenir de cette nébuleuse.
d) Conversion en km:
1 a.l=9,47x1012 km
D=9,47x1012 x2,9
D=2,746x1013 km
Le diamètre de la nébuleuse est de 2,746x1013 km. Son ordre de grandeur est de D=1013 km.
Exercice 4 : L'univers et le térahertz
Chacun connaît les rayons X, mais il existe aussi des rayons T.
Découverts depuis plus d’un siècle, les rayonnements térahertz ou rayons T sont restés longtemps une portion inexplorée du spectre électromagnétique. Il était en effet difficile de les détecter et de les produire.
Grâce aux avancées récentes de la technologie, ils connaissent aujourd’hui un engouement certain dans le domaine de l’imagerie médicale, la sécurité, la télécommunication à très haut débit, …

Données :
- Les fréquences des rayons térahertz sont comprises entre 0,1 THz et 30 THz ;
- 1 THz = 1012 Hz ;
- Célérité de la lumière : c = 3,00 × 108 m.s-1 ;
- Constante de Planck : h = 6,63 × 10–34 J.s ;
- Electron-volt : 1 eV = 1,60 × 10–19 J.
1. Térahertz et scanner
Les ondes térahertz possèdent des propriétés tout à fait remarquables. De part leur nature même, à la frontière de l’optique et des micro-ondes, leurs propriétés cumulent les avantages des deux mondes :
Elles peuvent pénétrer certains matériaux opaques au rayonnement visible tels que le carton, les tissus, le bois ou les matières plastiques ;
Elles interagissent peu avec la matière, ce qui permet de les utiliser dans des applications d’imagerie pénétrante sans toutefois présenter de danger pour les organismes vivants.
Les scanners à rayons X sont d’un usage courant. Dans les laboratoires, les chercheurs conçoivent de nouveaux types de scanner faisant appel aux rayons T.
1.1. Certains rayonnements sont dits ionisants. Leur énergie, supérieure à 10 eV, est suffisante pour transformer les atomes en ions. Ces rayonnements ionisants peuvent être nocifs pour les organismes vivants si la quantité d’énergie reçue est trop élevée.
1.1.1. Calculer l’énergie en eV :
D’un photon associé à un rayonnement X de fréquence égale à 1,0 × 1017 Hz ;
D’un photon associé à un rayonnement T de fréquence égale à 1,5 THz.
1.1.2. Comparer l’impact sur les organismes vivants d’un scanner à rayons X et d’un scanner à rayons T. Justifier la réponse.
1.2. Le pouvoir de résolution d’un système d’observation, est sa capacité à séparer deux points distincts pour qu’ils soient correctement discernés par l’observateur. Il est lié à la diffraction de l’onde, de longueur d’onde λ, lorsque l’onde traverse le système d’observation.
1.2.1. On éclaire une fente de largeur a par un laser de longueur d’onde λ.
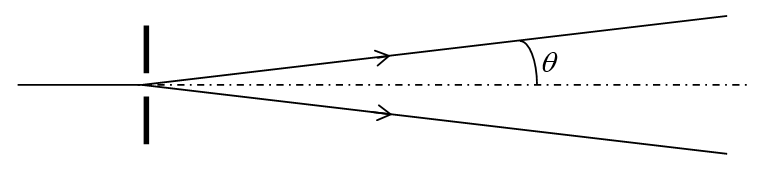
Rappeler l’expression reliant l’angle θ aux grandeurs a et λ.
1.2.2. Cette fente est maintenant éclairée par deux faisceaux laser faisant un angle a avec l’axe de la fente. On suppose que l’ouverture q du faisceau liée à la diffraction a la même expression que lorsque l’axe du faisceau arrive perpendiculairement à la fente.
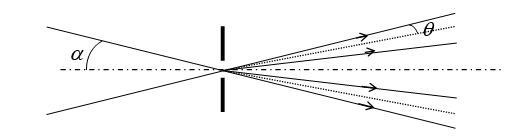
Montrer que si l’angle a est petit, il est impossible de séparer les deux faisceaux à la sortie de la fente. Donner l’expression de la valeur limite de a.
1.3. Plus le diamètre D de l’objectif de la caméra qui équipe le scanner est grand plus les détails observés sont petits. Un objet étant positionné est à une distance L de la caméra, on distingue deux points A et B de l’objet séparés d’une distance d si le diamètre Dmin de l’objectif de la caméra est au minimum de :
\[D_{min} = 1.22 \cdot \lambda \cdot \frac {L} {d}\]
1.3.1. Pour un objet situé à 12 cm de la caméra térahertz, sensible au rayonnement de fréquence égale à 1,5 THz, montrer que deux points séparés de 0,20 mm ne peuvent pas être distingués avec un objectif de diamètre 10 cm.
1.3.2. Comment modifier la valeur de la fréquence des ondes térahertz afin de visualiser distinctement ces deux points ?

2. Térahertz et étude de l’Univers
D’après les modèles construits par les chercheurs en astrophysique, la naissance de l’Univers s’est accompagnée de l’émission d’un intense rayonnement électromagnétique. Ce rayonnement nous parvient, atténué, après avoir cheminé des milliards d’années dans l’espace. Provenant de toutes les directions de l’Univers, ce « rayonnement fossile » apparaît homogène et se comporte comme le rayonnement d’un corps noir à la température de 3 kelvins.
Données :
Loi de Wien : λmax . T = 2,90.10–3 m.K
Avec λmax la longueur d’onde majoritairement émise (exprimée en m) dans le spectre d’émission d’un corps noir porté à une température T (exprimée en kelvin).
Absorption de l’atmosphère en fonction de la longueur d’onde de l’onde électromagnétique

2.1. Montrer que le « rayonnement fossile » peut être considéré comme un rayonnement térahertz.
2.2. Le rayonnement fossile peut-il être directement étudié avec des instruments au sol ou nécessite-t-il l’utilisation d’un satellite ? Justifier votre réponse.
Exercice 5 : Le goût de l'univers
Une équipe de l’institut Max Planck a braqué un radiotélescope sur le centre de notre galaxie. Le signal obtenu montre la présence d’une cinquantaine de molécules organiques différentes.

Les trois principales sont : l’aminoacétonitrile (NH2CH2CN) représenté figure 1, le méthanoate d’éthyle (HCOOC2H5) représenté figure 2 et le butanenitrile (C3H7CN), représenté figure 3.
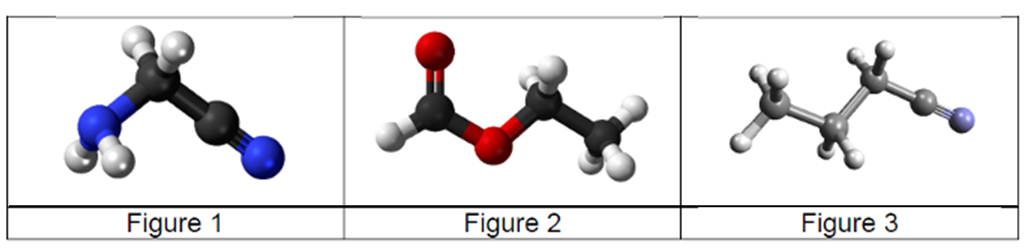
Le méthanoate d’éthyle est la molécule qui a suscité le plus d’intérêt : on la retrouve en grande partie dans les framboises et elle est à l’origine de l’odeur de rhum.
Données :
Masses molaires moléculaires :
| Espèce chimique | Acide méthanoïque | Ethanol | Méthanoate d’éthyle | Eau |
|---|---|---|---|---|
| Masse molaire (en g.mol-1) | 46 | 46 | 74 | 18 |
Table des données pour la spectroscopie infrarouge :
| Liaison | Nombre d’onde σ (cm-1) | Intensité |
|---|---|---|
| O – H | 3200 à 3600 | Forte |
| N – H | 3100 à 3500 | Moyenne |
| C – H | 2900 à 3100 | Moyenne |
| C = N | 2150 à 2250 | Forte |
| C = O | 1700 à 1750 | Forte |
| C – O | 1000 à 1250 | Forte |
| C – C | 1000 à 1200 | Moyenne |
1. Synthèse du méthanoate d’éthyle
Le méthanoate d’éthyle peut être synthétisé par réaction entre l’acide méthanoïque et l’éthanol en présence de quelques gouttes d’acide sulfurique.

1.1 Indiquer, en justifiant, à quelle famille chimique appartient le méthanoate d’éthyle.
1.2 Préciser le rôle de l’acide sulfurique introduit dans le mélange initial ainsi que son influence sur la réaction.
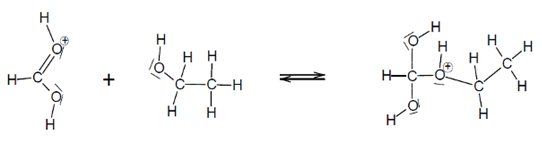
1.3 La réaction de synthèse se fait en plusieurs étapes. L’une des étapes est donnée ci-dessous et sur l’ANNEXE 2 à RENDRE AVEC LA COPIE.
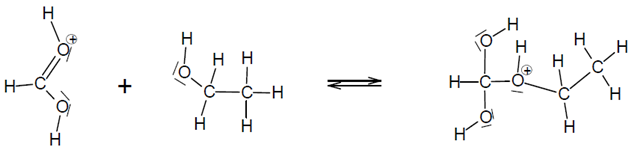
Après avoir identifié le site donneur et le site accepteur mis en jeu, représenter les flèches courbes rendant compte de cette étape sur l’ANNEXE 2 À RENDRE AVEC LA COPIE.
2. Calcul du rendement
On introduit dans le mélange initial 2,3 g d’acide méthanoïque et 2,8 g d’éthanol.
Déterminer le rendement h de la synthèse sachant qu’on obtient, après extraction, 1,9 g de méthanoate d’éthyle.
3. Analyse spectrale
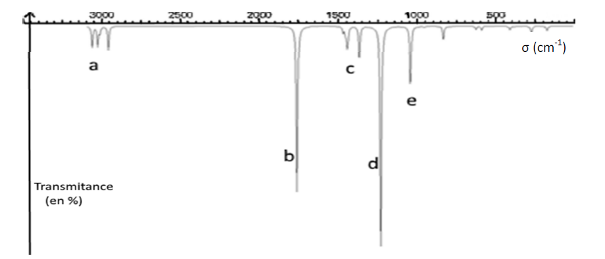
3.1. Une analyse du méthanoate d’éthyle donne le spectre infrarouge ci-après.
Identifier les liaisons correspondant aux bandes d’absorption a, b et d.
3.2. L’analyse spectrale IR peut être complétée par une spectroscopie de RMN du proton. Combien de signaux sont présents dans le spectre de RMN du méthanoate d’éthyle ? Préciser, en justifiant leur multiplicité.
Annexes
EXERCICE III : L’UNIVERS AURAIT UN GOÛT DE FRAMBOISE ET UNE ODEUR DE RHUM
Question 1.2.
Exercice 6 : Nucléosynthèse des éléments chimiques
Le but de cet exercice est d'étudier les réactions nucléaires qui se produisent dans l'univers, notamment dans les étoiles, et qui engendrent la synthèse des éléments chimiques.
Données:
- Masse d'un noyau d'hydrogène ou d'un proton: mp = 1,67 x 10-27 kg
- Masse d'un positron (ou positon) : me
- Célérité de la lumière dans le vide : c = 3,00 x 108 m.s-1
- Constante radioactive du "béryllium 8", λ ≈ 1 X 1016 s-1
- 1 eV = 1,60 x 10 -19 J
- Constante de Planck : h= 6,63 x 10-34 J.s
Certaines aides au calcul peuvent comporter des résultats ne correspondant pas au calcul à effectuer.
1. Les premiers éléments présents dans l'univers
Selon le modèle du big-bang, quelques secondes après l'explosion originelle, les seuls éléments chimiques présents étaient l'hydrogène (90%), l'hélium et le lithium, ce dernier en quantité très faible.
Les physiciens ont cherché à comprendre d'où provenaient les autres éléments existant dans l'univers.
1.1 Déterminer la composition des noyaux des atomes d'hélium et ainsi que celle de l'ion hélium.
1.2 La synthèse des éléments chimiques plus lourds se fait par des réactions nucléaires.
Pourquoi cette synthèse ne peut-elle pas se faire par des réactions chimiques ?
2. Fusion de l'hydrogène
Sous l'action de la force gravitationnelle les premiers éléments (hydrogène, hélium…) se rassemblent, formant des nuages gazeux en certains endroits de l'univers. Puis le nuage s'effondre sur lui-même et la température centrale atteint environ 107 K. Une étoile est née.
2.1 En notant mHe la masse d'un noyau d' "hélium 4", écrire l'expression littérale de l'énergie libérée lors de cette réaction de fusion des 4 noyaux d'hydrogène.
L'application numérique donne une valeur voisine de |ΔE| ≈ 4 x 10 -12 J
2.2 Cas du Soleil
2.2.1 À sa naissance on peut estimer que le Soleil avait une masse d'environ
MS = 2 x 1030 Seul un dixième de cette masse est constituée d'hydrogène suffisamment chaud pour être le siège de réactions de fusion. On considère que l'essentiel de l'énergie produite vient de la réaction de fusion précédente.
Montrer que l'énergie totale ET pouvant être produite par ces réactions de fusion est voisine de ET ≈ 1044 J.
2.2.2 Des physiciens ont mesuré la quantité d'énergie reçue par la Terre et en ont déduit l'énergie ES libérée par le Soleil en une année: ES ≈ 1034 J.an-1 .
En déduire la durée Δt nécessaire pour que le Soleil consomme toutes ses réserves d'hydrogène.
3. Un produit de la fusion de l'hélium
D'autres réactions de nucléosynthèse peuvent se produire au cœur d'une étoile. Selon les modèles élaborés par les physiciens, l'accumulation par gravitation des noyaux d'hélium formés entraîne une contraction du cœur de l'étoile et une élévation de sa température. Lorsqu'elle atteint environ 10 8 K, la fusion de l'hélium commence :

Il se forme ainsi des noyaux de "béryllium 8" radioactifs de très courte durée de vie.
On s'intéresse à la radioactivité du "béryllium 8". Soit N(t) le nombre de noyaux de "béryllium 8" présents dans l'échantillon à l'instant de date t, et N0 celui à l'instant de date t0 = 0 s.
En utilisant la loi de décroissance radioactive, démontrer la relation entre la demi-vie t1/2 et la constante radioactive \[\lambda : t_{1/2} = \frac {ln 2} {\lambda}\]
Exercice 7 : Regarder dans l'espace

Document 1 : Points de Lagrange
Dès 1923, Hermann Oberth mentionne l'intérêt d'un télescope spatial. En effet, un télescope terrestre reçoit des radiations filtrées par l'atmosphère terrestre qui absorbe des radiations électromagnétiques dans le domaine de l'infrarouge notamment. Par ailleurs un télescope spatial n'est pas sensible aux turbulences atmosphériques.
Le télescope spatial Hubble, du nom de l'astronome américain Edwin Hubble, a été lancé en 1990. Celui-ci souffrait au départ d'un défaut de courbure du miroir, non détecté avant la mise en orbite, qui provoquait des images floues. Après modification grâce à une mission spatiale, Hubble put enfin fournir ses premières images de l'Univers dans le domaine du spectre ultraviolet, visible et proche infrarouge. Le télescope Hubble, d'une masse m = 11 tonnes, est positionné sur une « orbite basse » à une altitude quasi constante h = 600 km de la surface de la Terre.
Le télescope spatial James Webb, du nom d'un administrateur de la NASA, doit succéder au télescope Hubble en 2018. Il sera lancé par une fusée Ariane 5. Le télescope spatial James Webb, d'une masse de 6200 kg, sera en orbite à une distance proche de 1,5 millions de kilomètres de la Terre en un point dénommé « point de Lagrange L2 » (voir documents 1 à 3).
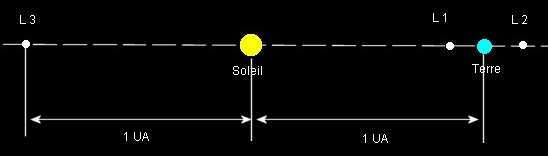
Document 2 : Positions des points de Lagrange sur l'axe Soleil-Terre
En mécanique céleste, il est un sujet qui a passionné de nombreux mathématiciens : c'est le problème dit « des trois corps ». Joseph-Louis Lagrange étudia le cas d'un petit corps, de masse négligeable, soumis à l'attraction de deux plus gros : le Soleil et, par exemple, une planète. II découvrit qu'il existait des positions d'équilibre pour le petit corps.
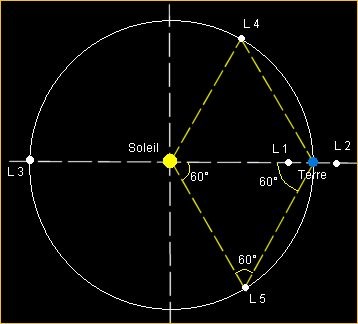
Un point de Lagrange (il en existe 5, notés L1 à L5) est une position de l'espace où les champs de gravité de deux corps très massifs en orbite l'un autour de l'autre fournissent exactement la force centripète requise pour que ce point de l'espace accompagne simultanément la rotation des deux corps.
Dans le cas où les deux corps sont en orbite circulaire, ces points représentent les endroits où un troisième corps de masse négligeable resterait immobile par rapport aux deux autres : il accompagnerait à la même vitesse angulaire leur rotation autour de leur centre de gravité commun sans que sa position par rapport à eux n'évolue. La sonde d'observation SoHO, destinée à observer le Soleil, a par exemple été placée au point L1.
Données :
- Constante de gravitation universelle : G = 6,67 x 10–11 m3.kg–1.s–2 ;
- Masse du Soleil : MS = 1,99 x 1030 kg ;
- Masse de la Terre : MT = 5,97 x 1024 kg ;
- Distance moyenne Soleil-Terre : d = 149,6 x 106 km équivaut à 1 UA (unité astronomique) ;
- Rayon de la Terre : RT = 6370 km ;
- Durée d'une année terrestre : 365,25 jours.
1. Première partie : étude de l'orbite du télescope spatial Hubble
On étudie le système {télescope spatial Hubble} dans le référentiel géocentrique en négligeant l'interaction gravitationnelle du Soleil avec le télescope.
1.1. Quelle est la trajectoire du télescope Hubble dans ce référentiel ?
1.2. À partir de la deuxième loi de Newton, montrer que, dans l'approximation d'une trajectoire circulaire, le mouvement du télescope Hubble est uniforme.
1.3. Montrer que l'expression de la valeur de la vitesse v du satellite dans le référentiel géocentrique est : \[v = \sqrt {\frac{G \cdot M_{T}}{R_{T} + h}}\]
1.4. Établir l'expression de sa période de révolution T en fonction de RT, h et v.
1.5. Rappeler la troisième loi de Kepler.
Montrer que dans le cas du télescope spatial Hubble on a la relation : \[\frac{T^{2}}{r^{3}} = \frac{4 \pi ^{2}}{G \cdot M \cdot _{T}} \]
où r = RT + h représente la distance entre le centre de la Terre et le télescope spatial.
1.6. Calculer la période de révolution T du télescope spatial Hubble, exprimée en minutes.
2. Deuxième partie : étude de la mise en orbite du télescope spatial James Webb
Le télescope spatial James Webb sera mis en orbite par le lanceur européen Ariane 5 depuis la base de lancement située à Kourou en Guyane. Dans cette partie on étudie tout d'abord le système {Ariane 5} (incluant tout son équipement y compris le télescope) dans le référentiel terrestre que l'on suppose galiléen pendant la durée de l'étude. Initialement le système {Ariane 5} est situé sur sa base de lancement. Le repère d'espace choisi est un axe vertical Oz orienté vers le haut. L'origine O est initialement confondue avec le centre d'inertie de la fusée de sorte que z(0) = z0 = 0.
2.1. Lors de son décollage, la fusée Ariane 5 et son équipement possèdent une masse totale proche de M = 780 tonnes. La valeur F de la force de poussée générée par ses propulseurs est de l'ordre de 14,0 x 106 N.
2.1.1 Déterminer la valeur P du poids de la fusée Ariane 5 au moment de son décollage. Donnée : g = 9,8 m.s -2(intensité de la pesanteur).
2.1.2 Déduire de la deuxième loi de Newton l'expression de la coordonnée aZ du vecteur accélération du lanceur Ariane 5 au moment de son décollage en fonction de M, F et g.
2.1.3 L'accélération reste constante si l'on peut négliger les forces de frottement fluide et si le champ de gravitation reste constant. On montre que l'altitude z(t) du lanceur Ariane 5 est alors donnée par la relation :\[z (t) = \frac{1}{2} \cdot (\frac{F}{M} - g ) t^{2}\]
Calculer la valeur de l'altitude z du lanceur Ariane 5 au bout de 10 s dans ces conditions.
2.1.4 En réalité, l'altitude d'Ariane 5 est nettement plus faible au bout de 10 s. Proposer une explication énergétique.
On envisage à présent le cas où le télescope James Webb aura atteint le point de Lagrange L2.
2.2. Pourquoi le point L2 a-t-il été choisi pour l'orbite du télescope James Webb plutôt que le point L1, alors qu'il est envisageable de placer plusieurs satellites au même point de Lagrange ?
Résumer avec l'IA :






















Si vous désirez une aide personnalisée, contactez dès maintenant l’un de nos professeurs !