Chapitres
- 01. Les différents champs
- 02. Le théorème de superposition
- 03. Théorème de Gauss
- 04. Équation de Maxwell-Gauss
- 05. Équation de Poisson
- 06. Problématique
- 07. Analyse
- 08. Réalisation
- 09. Validation
- 10. Exercice pour s'entraîner

Les différents champs
Champ électrique
En physique, on appelle champ électrique tout champ vectoriel créé par des particules électriquement chargées. Plus exactement, lorsque nous sommes en présence d'une particule chargée, les propriétés locale de l'espace défini sont alors modifié ce qui permet de définir la notion de champ. En effet, si une autre charge se trouve être dans le dit champ, elle subira ce qu'on appelle l'action de la force électrique qui est exercée par la particule malgré la distance. On dit alors du champ électrique qu'il est le médiateur de la dite action à distance. Si on se veut plus précis, on peut définir dans un référentiel galiléen défini, une charge q définie de vecteur vitesse v qui subit de la part des autres charges présentes, qu'elles soient fixes ou mobiles, une force qu'on définira de force de Lorentz.

On appelle référentiel galiléen tout référentiel au sein duquel le principe d'inertie est vérifié.
Cette force se décompose ainsi : 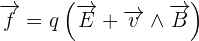 avec :
avec :
 le champ électrique. Celui-ci décrit dans ce cas la partie de la force de Lorentz qui est indépendante de la vitesse de la charge
le champ électrique. Celui-ci décrit dans ce cas la partie de la force de Lorentz qui est indépendante de la vitesse de la charge le champ magnétique. Celui-ci décrit ainsi la partie de la force exercée sur la charge qui dépend du déplacement de cette même charge dans le référentiel choisi.
le champ magnétique. Celui-ci décrit ainsi la partie de la force exercée sur la charge qui dépend du déplacement de cette même charge dans le référentiel choisi.
De plus, il est important de noter que les deux champs, électrique et magnétique, dépendent du référentiel d'étude. Avec cette formule, on peut alors définir le champ électrique comme étant le champ traduisant l'action à distance subie par une charge électrique fixe dans un référentiel défini de la part de toutes les autres charges, qu'elles soient mobiles ou fixes. Mais on peut également définir le champ électrique comme étant toute région de l'espace dans laquelle une charge est soumise à une force dite de Coulomb. On commence à parler de champ électrostatique lorsque, dans un référentiel d'étude, les charges sont fixes. Notons d'ailleurs que le champ électrostatique ne correspond pas au champ électrique comme décrit plus haut dans cet article puisqu'en effet, lorsque les charges sont en mouvement dans un référentiel, il faut ajouter à ce référentiel un champ électrique qui est induit par les déplacement des charges afin d'obtenir un champ électrique complet. Mais, le champ électrique reste dans la réalité un caractère relatif puisqu'il ne peut exister indépendamment du champ magnétique. En effet, si on observe la description correcte d'un champ électromagnétique, celui-ci fait intervenir un tenseur quadridimensionnel de champ électromagnétique dont les composantes temporelles correspondent alors à celle d'un champ électrique. Seul ce tenseur possède un sens physique. Alors, dans le cas d'un changement de référentiel, il est tout à fait possible de transformer un champ magnétique en champ électrique et inversement.
Champ électromagnétique
En physique, on appelle champ électromagnétique la représentation dans l'espace d'une force électromagnétique exercée par des particules chargées. Ce champ représente alors l'ensemble des composantes de la force électromagnétique qui s'appliquent à une particule chargée qui se déplace alors dans un référentiel galiléen. On peut alors définir la force subit par une particule de charge q et de vecteur vitesse par l'expression suivante : 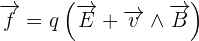 avec :
avec :  le champ électrique. Celui-ci décrit dans ce cas la partie de la force de Lorentz qui est indépendante de la vitesse de la charge
le champ électrique. Celui-ci décrit dans ce cas la partie de la force de Lorentz qui est indépendante de la vitesse de la charge  le champ magnétique. Celui-ci décrit ainsi la partie de la force exercée sur la charge qui dépend du déplacement de cette même charge dans le référentiel choisi. En effet la séparation de la partie magnétique et de la partie électrique de dépend que du point de vue pris selon le référentiel d'étude. De plus, il peut être intéressant de savoir que les équations de Maxwell régissent les deux composantes couplées, c'est à dire électrique et magnétique, de sorte que toute variation d'une composante induira la variation de l'autre composante. D'ailleurs, le comportement des champs électromagnétiques se trouve décrit de façon classique par les équations de Maxwell et de manière plus générale par l'électrodynamique quantique. La façon la plus utilisée afin de définir le champ électromagnétique est celle du tenseur électromagnétique de la relativité restreinte.
le champ magnétique. Celui-ci décrit ainsi la partie de la force exercée sur la charge qui dépend du déplacement de cette même charge dans le référentiel choisi. En effet la séparation de la partie magnétique et de la partie électrique de dépend que du point de vue pris selon le référentiel d'étude. De plus, il peut être intéressant de savoir que les équations de Maxwell régissent les deux composantes couplées, c'est à dire électrique et magnétique, de sorte que toute variation d'une composante induira la variation de l'autre composante. D'ailleurs, le comportement des champs électromagnétiques se trouve décrit de façon classique par les équations de Maxwell et de manière plus générale par l'électrodynamique quantique. La façon la plus utilisée afin de définir le champ électromagnétique est celle du tenseur électromagnétique de la relativité restreinte.
Le théorème de superposition
Ce théorème est permis par la linéarité des équations de Maxwell. Il est possible d'appliquer le principe de superposition à un système de type entrée-sortie si :
- La somme de deux entrées quelconque correspond à la somme des deux sorties correspondantes ;
- Un multiple d'une entrée quelconque correspond le même multiple de la sortie correspondante.
Dans ce cas, c'est-à-dire celui d'un système physique, on peut appeler l'entrée excitation et la sortie réponse. On obtient alors, en notant les excitations ƒ et les réponses x (donc les mouvements généré par les forces mécaniques ƒ) :
- Lorsque l'on sollicite le système par une entrée, donc une excitation notée ƒ1, une réponse, donc un déplacement, qui sera noté x1 ;
- Lorsque l'on sollicite le système par une entrée, donc une excitation notée ƒ2, une réponse, donc un déplacement, qui sera noté x2.
Théorème de Gauss
Le théorème de Gauss permet, en électromagnétisme, de calculer le flux d'un champ électrique à travers une surface qui est fermée et ce grâce à la connaissance des charges électriques que cette surface renferme. Il s'énonce ainsi :
Le flux du champ électrique à travers une surface S fermée est égal à la somme des charges électriques contenues dans le volume V délimité par cette surface, divisée par la permittivité du vide.

Équation de Maxwell-Gauss
Les équations de Maxwell-Gauss, aussi connues sous le noms d'équations de Maxwell-Lorenz sont des équations fondamentales de la physique. En effet, ces sont elles qui régissent l'électromagnétisme. Elles tiennent leur nom du physicien James Clerk Maxwell d'origine écossaise. Toute sa vie il a travaillé sur les champs électriques et magnétiques et il a également contribué à l'élaboration de nombreuses lois physiques dans son domaine. Il est considéré comme l'un des scientifiques les plus influents du IXXème siècle. Elle réunit sous la forme d'équations intégrales des lois déjà connues telles que celles de théorèmes de Gauss, Ampère et Faraday. Les équation de Maxwell sont essentielles puisqu'elles démontrent qu'en régime stationnaire, les champs électrique et magnétiques sont indépendants l'un de l'autre, ce qui n'est pas nécessairement le cas lorsque l'on se trouve en régime variable. En effet, dans le cas le plus général, il faut alors parler du champ électromagnétique puisque la séparation entre l'électrique et le magnétique n'est qu'un aspect visualisé par l'Homme.
Équation de Poisson
L'équation de Poisson est une équation aux dérivées partielles de cette forme : 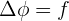 Appliqué à l'électrostatique, elle donne le potentiel électrique appelé V en présence d'une d'une distribution de charges p :
Appliqué à l'électrostatique, elle donne le potentiel électrique appelé V en présence d'une d'une distribution de charges p : 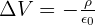 Cette équation est nommé ainsi en hommage au physicien et mathématicien Siméon Denis Poisson. D'origine française, il est célèbre pour ces nombreux travaux dans plusieurs matières scientifiques. Il a marqué l'histoire de la physique avec ses recherches sur l'électricité et les potentiels. Il a aussi participé aux travaux mathématiques concernant les intégrales et notamment les intégrales de Fourier.
Cette équation est nommé ainsi en hommage au physicien et mathématicien Siméon Denis Poisson. D'origine française, il est célèbre pour ces nombreux travaux dans plusieurs matières scientifiques. Il a marqué l'histoire de la physique avec ses recherches sur l'électricité et les potentiels. Il a aussi participé aux travaux mathématiques concernant les intégrales et notamment les intégrales de Fourier.
Problématique
But de l'électromagnétisme : décrire les interactions entre distributions de charges.
Pas d’interaction à distance, le champ électromagnétique (E, B) est l'intermédiaire de l’interaction : -> savoir décrire le champ créé par une distribution de charges -> savoir décrire l'action de ce champ sur l'autre distribution de charges Question : quel lien géométrique entre le champ électromagnétique (E, B) et ses sources ?

Analyse
E et B n'ont pas le même statut : E est un "vrai" vecteur, indépendant d'une convention mathématique, les symétries des sources se retrouvent dans les symétries du champ, B est un "pseudo-vecteur", dépendant d'une convention mathématique, les symétries des sources ne se retrouvent pas dans les symétries du champ.
Réalisation
1 - Caractère polaire polaire de E, caractère axial de B
2 - Plans de symétrie et d'antisymétrie des sources
3 - Conséquence sur les champs a - en un point appartenant à un plan de symétrie ou antisymétrie des sources b- en des points symétriques par un plan de symétrie ou d'antisymétrie des sources.

Validation
Analyse par symétries et par superposition de champs élémentaires :
- Spectre d'une charge ;
- Spectre d'un dipôle ;
- Spectre d'une spire.
Exercice pour s'entraîner
1. Étude comparative des dipôles RL, RC et RLC série.
On réalise successivement les circuits correspondant aux montages 1, 2 et 3.
Dans le montage 1, le condensateur est initialement déchargé, alors que dans le montage 3, il est initialement chargé. Le sens positif de l’intensité du courant i est indiqué sur les schémas.
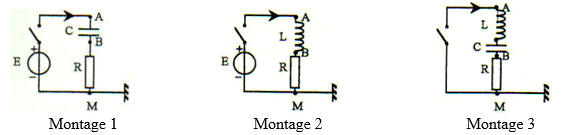
1.1. On visualise à l’aide d’un système approprié la tension uR aux bornes du conducteur ohmique.
1.1.1. Préciser entre quels points on doit réaliser le branchement.
1.1.2. Expliquer pourquoi on visualise alors les variations de l’intensité du courant.
1.2.On ferme l’interrupteur et on observe, à partir des montages précédents, les oscillogrammes a, b et c.
Le trait pointillé correspond à la trace du spot en l’absence de tension sur les deux voies.
Affecter à chaque montage l’oscillogramme correspondant. Justifier brièvement les réponses.

2. Exemple d’application : flash d’appareil photographique jetable.
Certains appareils photographiques sont équipés d’un flash dont le principe de fonctionnement est expliqué ci-dessous.

1ère phase
A la fermeture de l’interrupteur K1, la pile alimente l’oscillateur qui délivre alors une tension alternative ; celle-ci peut être élevée
grâce au transformateur ; le redresseur permet d’obtenir une tension continue de l’ordre de quelques centaines de volts entre les points P et N. Le condensateur se charge et emmagasine alors de l’énergie.
2nde phase
Au moment où le photographe appuie sur le déclencheur, l’interrupteur K2 se ferme et le condensateur libère alors quasi instantanément l’énergie emmagasinée dans la lampe, ce qui produit un flash lumineux.
Le schéma équivalent au schéma de principe de la page précédente est représenté ci-contre.

Données :
- C = 100 mF ;
- uC : tension aux bornes du condensateur ;
- + : sens positif du courant dans la branche AB.
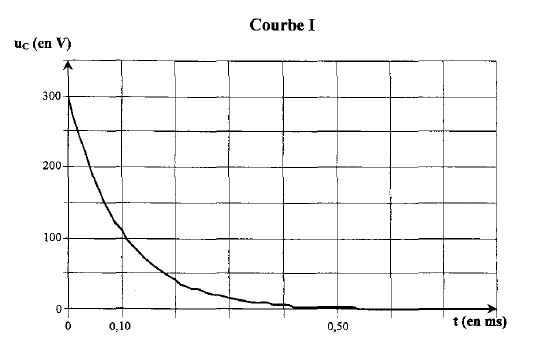
Une étude expérimentale du dispositif a permis d’obtenir les courbes I et II de l’annexe, à rendre avec la copie.
2.1. Identification des courbes.
2.1.1. Associer à chaque phase de fonctionnement du flash décrite page précédente, les phénomènes de charge et de décharge du condensateur.
2.1.2. Affecter à chacune des courbes (I et II) la phase correspondante.
2.2. Évolution temporelle du système lors des deux phases.
Les courbes I et II de l’annexe permettent d’évaluer graphiquement la constante de temps t lors de chacune des phases.
Expliquer et utiliser une méthode au choix permettant de déterminer τ.
Vérifier sur l’annexe qu’on obtient : τ (courbe I) = 0,1 ms et τ (courbe II) = 3 s.
En déduire les valeurs approchées de R et de r.
2.3. Puissances mises en jeu lors des deux phases.
La puissance moyenne P, mise en jeu lors d’un échange d’énergie DE pendant la durée Dt, est donnée par : 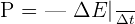
Avec ΔE en joules, Δt en secondes et P en watts.
2.3.1. Quelle est la tension maximale aux bornes du condensateur ?
2.3.2. En déduire l’énergie maximale emmagasinée dans le condensateur.
2.3.3. On considère que la charge ou la décharge est complète à t = 5τ.
Utiliser les valeurs indiquées au paragraphe 2.2.2. pour calculer la puissance moyenne mise en jeu lors de chaque phase. Quel est l’intérêt pratique de la différence constatée ?
En déduire pourquoi la résistance r du tube éclair doit être petite.
2.4. Étude théorique du dispositif utilisé.
2.4.1. Préciser le signe des charges portées par chacune des armatures du condensateur lorsqu’il est chargé. Indiquer, lors de chaque phase, si le courant circule dans la branche AB dans le sens positif choisi en justifiant brièvement.
2.4.2. Établir l’équation différentielle vérifiée par uC c’est-à-dire la relation entre la fonction uC(t) et sa dérivée par rapport au temps lors de chacune des phases de fonctionnement.
Annexe à rendre avec la copie
Résumer avec l'IA :






















Si vous désirez une aide personnalisée, contactez dès maintenant l’un de nos professeurs !
Bonjour ;
il est sympa ; votre site ! Beaucoup de choses à voir et à savoir… je le mets dans mes favoris, et je reviendrais sûrement.
Bonne continuation et longue vie à votre blog !
[url=http://www.ysalis-voyance.com]voyance gratuite par email[/url]