Chapitres
- 01. La résistance
- 02. La Loi d'Ohm
- 03. La Loi de Joule
- 04. Analyse
- 05. L'énergie potentielle électrique
- 06. Loi de Coulomb
- 07. Exercice d'application

La résistance
La résistance désigne la capacité physique d'un matériau à s'opposer au passage d'un courant électrique sous une certaine tension. C'est de là que sont nés les composants électriques appelés les résistances.

La Loi d'Ohm
La tension électrique entre les bornes d'une résistance électrique est égale au produit de la valeur de sa résistance par l'intensité du courant qui la traverse d'où la relation U = R x I.
Avec :
- U : intensité en Volts ;
- R : résistance en Ohms ;
- I : intensité en Ampères.
On a alors ceci :
[ upsilon _ { R } = R times i ] [ L C \frac { text{ d} ^ { 2 } U c } { text{ d} t ^ { 2 } } + R C \frac { text{ d} ^ { 2 } U c } { text{ d} t ^ { 2 } } + upsilon _ { c } = 0 ] [ \frac { text{ d} ^ { 2 } U c } { text{ d} t ^ { 2 } } + \frac { R } { L } \frac { text{ d} U c } { text{ d} t } + \frac { 1 } { LC } upsilon _ { c } = 0 ]
Ce qui signifie que la tension aux bornes du conducteur ohmique est égale au produit de la valeur du résistance par l'intensité du courant qui le traverse. La caractéristique intensité tension (U en fonction de I) est une droite qui passe par l'origine des axes. Son coefficient directeur est égal à la valeur de la résistance. Un fil électrique est un conducteur ohmique, il doit avoir la plus petite résistance possible. Matériaux avec une résistance faible : métaux (surtout le cuivre, ensuite l'aluminium et enfin le fer). Matériaux avec une résistance très élevée : isolants. Plus la résistance est élevée, plus il est difficile de faire passer un courant.

La Loi de Joule
La loi de Joule correspond à une loi qui permet de définir le dégagement d'énergie, dissipée sous forme de chaleur, d'un résistor ou résistance qui se trouve parcouru par un courant électrique. Ainsi, pour une résistance de résistivité R traversée par un courant d'intensité i, on obtient les relations suivantes : [ P = R times i ^ { 2 } = P _ { J } ] Et donc : [ E = R times i ^ { 2 } times t ] Où :
- E, représentant l'énergie, est exprimé en joules ;
- R, représentant la résistivité de la résistance, est exprimée en ohms ;
- i, représentant l'intensité du courant, est exprimée en ampères ;
- Et t, représentant le temps, est exprimé en secondes.
La Joule
La Joule est une unité du Système International qui sert à définir l'énergie.
Le système international d'unités, abrégé en SI, est le système décimal des unités de mesures le plus utilisé au monde. L’ensemble des unités associées aux dimensions fondamentales constitue le système international d’unités. Il s’agit du système MksA (mètre, kilogramme, seconde, Ampère), mais le Kelvin, la mole et le candela font aussi partie de ce système. Ces unités sont appelées unités légales. Elles sont universelles et connues de par le monde entier.

Analyse
- L'existence d'une différence de potentiel aux bornes d'un conducteur est le signe de l'existence d'un champ électrique dans le conducteur, l'existence d'un courant est le signe d'un déplacement des charges libres du conducteur ;
- La loi d'ohm pour un conducteur ohmique traduit la linéarité macroscopique du matériau : la cause est la tension appliquée, la conséquence est le courant qui circule ;
- Microscopiquement, la cause est le champ électrique dans le conducteur, la conséquence est le déplacement des charges libres ;
- Mésoscopiquement, la linéarité du matériau s'exprime donc par la proportionnalité entre le champ électrique local (la cause) et le vecteur densité de courant (la conséquence) ;
- La puissance électrique absorbée par une portion de circuit est en fait la puissance fournie aux porteurs de charges par le champ électrique. Mésoscopiquement elle fait donc intervenir le vecteur densité de courant et le champ électrique ;
- La puissance électrique absorbée par une conducteur est quadratique, on doit retrouver cet aspect quadratique dans la loi locale.
L'énergie potentielle électrique
L'énergie potentielle électrique, encore appelée énergie électrostatique, correspond à une énergie potentielle mesurée en joules qui résulte alors des forces de Coulomb. On y associe également la configuration d'un ensemble particulier de charges électriques ponctuelles dans un système défini : on peut parler de champ électrostatique. L'énergie potentielle électrique d'un objet dépendra alors de deux paramètres bien définis qui sont : l'énergie de l'objet et sa position par rapport à d'autres objets qui peuvent être chargés électriquement. Ce type d'énergie, c'est-à-dire l'énergie potentielle électrique, correspond à l'énergie qui est utilisée au sein des condensateurs.
Loi de Coulomb
Coulomb, un physicien français, a établi en 1758 que le champ doit varier comme le carré inverse de la distance entre les charges à une précision de 0,02 sur l'exposant avec l'aide d'un dispositif appelé balance de Coulomb. Cette balance est constituée d'un fil de torsion en argent sur lequel est fixé des matériaux chargés. Ainsi, la loi d'attraction entre deux charges ponctuelles notées q1 et q2 , fixes dans le référentiel défini et séparées par une distance r, se définit ainsi :
- La force est dirigée selon la droite reliant les deux charges ;
- Elle est attractive si les charges sont de signes opposée et répulsive sinon ;
- Son intensité est proportionnelle aux valeurs de q1 et q2 et varie en raison inverse du carré de la distance r.
Ce qui peut rendre la compréhension de cette formule compliquée est la notion de force à distance. En effet, comment une charge peut savoir qu'une autre charge ponctuelle se trouve à une certaine distance d'elle et alors exercer sur force sur cette charge en fonction de la distance qui les sépare. Dans ce cas, tout comme pour un champ gravitationnel, il peut être utile de séparer dans la loi de force ce qui dépend de la charge subissant la force.
Ainsi, avec cette relation, il est plus aisé d'interpréter l’existence d'une force à distance. En effet, la charge considérée comme "source", c'est-à-dire q1, crée en tout point de l'espace un champ électrique dont la forme est donnée par la relation exprimée ci-dessus, et une charge quelconque considérée comme "test" subira l'effet de ce champ sous la forme d'une force égale au produit de cette charge par le champ électrostatique. Dans ce cas, ce champ électrostatique apparaîtra comme la force entre deux particules ponctuelles fixes par unité de charge.
Exercice d'application
Cet exercice est un Questionnaire à Réponses Ouvertes et Courtes. A chaque affirmation, vous répondrez par VRAI ou FAUX. Toute réponse doit être accompagnée de justifications ou de commentaires brefs (définitions, calculs, exemples ou contre-exemples ...).

Question 1
On a réalisé le montage ci-dessous avec les composants suivants : un conducteur ohmique de résistance
R = 4,0 x 102 W, une bobine d’inductance L = 0,40 H (résistance interne de la bobine négligée) et un condensateur de capacité C = 1,0. 10-6 F.
On charge le condensateur, commutateur basculé en position 1, puis, à l’instant de date t0 = 0, le commutateur est basculé en position 2.
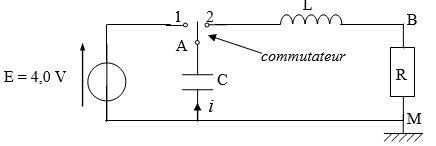
Les points A, B et M sont reliés à un ordinateur ou à un système d’acquisition. Grâce à un logiciel adapté on observe l’évolution des tensions au cours du temps (schéma ci-après).
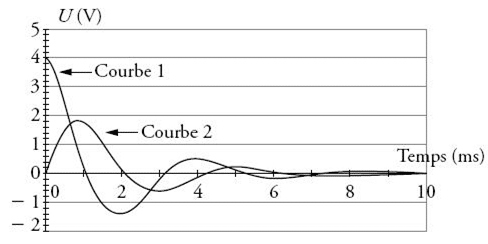
1. A propos des courbes
La courbe 1 visualisée est :
- La tension aux bornes du condensateur ;
- La tension aux bornes du conducteur ohmique ;
- La tension aux bornes de la bobine.
La courbe 2 visualisée est :
- La tension aux bornes de la bobine ;
- La tension aux bornes du conducteur ohmique ;
- A propos des énergies.
A l’instant initial le circuit RLC a emmagasiné une énergie E1 de :
- 8,0 mJ ;
- 8,0. 10-6 J ;
- 2,0. 10-6 J.
Lorsque les deux courbes se coupent pour la première fois, la valeur de l’intensité du courant vaut :
- 5,0 mA ;
- 7,7 mA ;
- 4,2 mA.
4. Lorsque les deux courbes se coupent pour la première fois, la somme des énergies emmagasinée dans la bobine et dans le condensateur notée E2 est :
- 7,0. 10-6 J ;
- 5,0. 10-6 J ;
- 2,0. 10-6 J.
5. Lorsque les deux courbes se coupent pour la première fois, l’énergie qui a été dissipée dans la résistance vaut :
- 3,0. 10-6 J ;
- 1,0. 10-3 J ;
- 10 mJ.
Question 2
On donne le graphe représentant en fonction du temps l’énergie cinétique et l’énergie potentielle élastique d’un système solide–ressort horizontal, écarté de sa position d’équilibre, lâché sans vitesse initiale à l’instant t = 0 s et à l’abscisse x0.
L’origine des abscisses correspond à la position d’équilibre du système.
1. La courbe correspondant à l’énergie cinétique est représentée en trait plein.
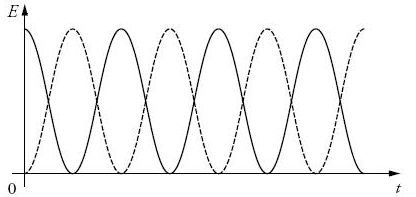
2. On suppose que l’énergie potentielle de pesanteur est nulle au niveau horizontal où se situe le système. Le système de masse m, comporte un ressort de raideur k.
L’expression de l’énergie mécanique du système est donnée par l’expression :
[ E _ {m} = \frac {1} {2} k ^{2} _ {0} ]
3. L’allure des courbes permet d’affirmer qu’il n’y a pas de frottements.
Question 3 :
On dispose d’une solution de nitrate d’argent Ag+(aq) + NO3-(aq) de concentration 0,10 mol.L-1, d’une solution de sulfate de cuivre de concentration 0,50 mol.L-1, d’un fil d’argent, d’une lame de cuivre et d’un pont salin au nitrate de potassium.
On peut former une pile par l’association des couples Ag+(aq) / Ag(s) et Cu2+(aq) / Cu(s).
Soit l’équation de réaction : 2 Ag+(aq) + Cu(s) = 2 Ag(s) + Cu2+(aq)
La constante d’équilibre est K = 2,0.1015.
1. On relie les deux métaux constituant les bornes de la pile par une chaîne conductrice, le quotient de réaction initial de ce système, pour l’équation donnée est :
- Qr, i = 50, alors la réaction est spontanée dans le sens direct.
- Qr, i = 50, alors la réaction est spontanée dans le sens inverse.
- Qr, i = 0,02, alors la réaction est spontanée dans le sens direct.
- Qr, i = 0,02, alors la réaction est spontanée dans le sens inverse.
2. Lorsque cette pile fonctionne (ou débite) son quotient de réaction :
- Augmente ;
- Diminue ;
- Ne varie pas.
3. Quel est le pôle négatif de la pile :
- L’électrode d’argent ?
- L’électrode de cuivre ?
Question 4 :
Une pile de ce type a une f.é.m. E = 2,0 V ; elle est prévue pour fonctionner pendant 10 h si elle débite de manière constante un courant d’intensité 320 mA.
Données :
- 1 F = 9,65.104 C.mol-1.
4. L’énergie maximale disponible de cette pile est égale à :
- 11,5 J ;
- 1,15.104 J ;
- 2,30.104
5. La quantité d’électrons qui circulent pendant la durée totale du fonctionnement est égale à :
- 0,12 mol ;
- 1,0 mol ;
- 2,0 mol.
Résumer avec l'IA :






















Si vous désirez une aide personnalisée, contactez dès maintenant l’un de nos professeurs !
Relations entre vitesse débit intensité temps conducteur ohmique