Chapitres

Présentation
Le théorème de Bernoulli est une théorème physique qui a été énoncé en 1738 par Daniel Bernoulli. Il parle des mouvements des fluides, d'hydrostatique et de dynamique des fluides. On en retire notamment que la vitesse augmente en cas de baisse de pression sur un fluide homogène et incompressible. Aujourd'hui, ce théorème est fortement utilisé dans l'aérodynamique afin de régler des problèmes de portance.
Daniel Bernoulli

Daniel Bernoulli est un médecin suisse ayant vécu entre 1700 et 1782. En parallèle de l'exercice de son métier de médecin, il était aussi physicien et mathématicien. On lui de nombreuses lois et théorèmes dans ces deux domaines. Il sera même récompensé par l'Académie des sciences de Paris pour ses travaux. Il a expliqué des phénomènes comme les marées et il a laissé derrière lui le théorème de Bernoulli qui traite de la mécanique des fluides ainsi que la théorie cinétique des gaz. Durant toute sa vie, il a enseigné dans de nombreuses académies, notamment l'Académie royale des sciences de Paris le 24 juin 1748, l'Académie royale des sciences de Prusse, la Royal Society de Londres, l'Académie des sciences de l'institut de Bologne, l'Académie des sciences de Saint-Pétersbourg, l'Académie des sciences de Mannheim, l'Académie des sciences de Turin ainsi que la société économique de Berne.
Analyse
- Les théorèmes de la mécanique et de la thermodynamique sont énoncés en PCSI pour des systèmes fermés. Dans le cas d'un système ouvert, il faudra veiller à appliquer ces théorèmes à une partie fermée du système ouvert : on obtient alors une nouvelle formulation des théorèmes de la mécanique et de la thermodynamique pour les systèmes ouverts.
- Dans le cas du théorème de Bernoulli, on utilise le théorème de l'énergie cinétique, ou plus exactement le théorème de l'énergie mécanique, dans le cas d'un écoulement parfait, incompressible et stationnaire.
La mécanique des fluides : les notions à comprendre
La mécanique des fluide est une matière de la physique qui consiste en l'étude des différents fluides qui peuvent être sous forme liquide, gazeuse ou de plasma.
Le plasma est un état de la matière, au même titre que l’état gazeux, l’état liquide ou encore l’état solide. Il se constitue en grandes parties de particules ionisées. Il a été introduit comme quatrième état de la matière en 1928 par le physicien américain Irving Langmuir. On peut le rencontrer sur Terre sous de très hautes températures. Le cœur des flammes, la foudre ou encore les étoiles sont sous l’état de plasma
La mécanique des fluides s'articule autour de deux grandes études : l'étude de l'hydrostatique et celle de la dynamique des fluides.

L'hydrostatique est l’étude des fluides immobiles. Elle est également nommée statique des fluides. C'est le savant Archimède qui l'a mise au point. Elle définit l'étude de nombreux phénomènes physiques de la mécanique des fluides avec notamment les notions de pression dans un fluide, du cas particulier où ce dernier serait incompressible également. C'est grâce à cette discipline qu'on a pu mettre au point le baromètre qui permet de mesurer la pression atmosphérique. Aujourd'hui, on utilise l'hydrostatique pour de nombreuses applications :
- Mesure de la pression de l'air et de l'eau ;
- Mesure de la masse volumique ;
- Météorologie et climatologie.
La dynamique des fluides est l'étude des fluides en mouvement. Cette dernière caractérise les fluides qu'ils soient liquides ou gazeux en leur donnant diverses propriétés :
- Vitesse d'un fluide ;
- Viscosité d'un fluide ;
- Densité d'un fluide ;
- Pression d'un fluide ;
- Température d'un fluide.
Propriétés d'un fluide

On appelle viscosité l'ensemble des phénomènes de résistance à l'écoulement qui peuvent se produire dans la masse d'une matière dans le cas d'un écoulement que l'on considère comme étant uniforme et sans turbulence. De façon logique, plus le viscosité sera élevée, plus la capacité que possède le fluide à s'écouler facilement va diminuer. De plus, lorsque la viscosité est élevée, l'énergie qui sera dissipée par l'écoulement sera importante. La viscosité de cisaillement, qui peut être comprise comme une résistance à l'écoulement des différentes couches d'un fluide les unes sure les autres, englobe plusieurs grandeurs physiques qui permettent de la caractériser :
- La viscosité dynamique qui est la grandeur la plus utilisée. En effet, on se réfère généralement à cette grandeur lorsque l'on parle de viscosité sans précision. Elle permet de faire le lien entre la contrainte de cisaillement et le gradient transversal de la vitesse d'écoulement dans la matière. C'est donc pour cela que l'on appelle cette grandeur vitesse dynamique.
- La viscosité cinématique, cette grandeur peut être déduise de la vitesse dynamique ;
- La seconde viscosité qui caractérise la résistance du fluide à des variations de volume ;
- Et pour finir, la viscosité de volume qui correspond à la combinaison de la viscosité dynamique et la seconde viscosité.
De ce fait, on peut considérer la viscosité comme correspondant à une quantité tensorielle bien qu'il reste possible que, selon les cas, on puisse exprimer cette grandeur sous la forme d'une grandeur scalaire. La viscosité (de cisaillement) peut être vue comme la résistance à l'écoulement des différentes couches d'un fluide les unes sur les autres. Plusieurs grandeurs physiques caractérisent la viscosité: En ce qui concerne les liquides, alors que l'inverse est vrai pour les gaz, la viscosité va tendre, de façon générale, à diminuer lorsque la température va augmenter. De plus, croire que la viscosité d'un fluide donné augmente avec la densité est faux car ce n'est pas nécessairement vrai. On peut en effet prendre l'exemple de l'huile qui, pourtant moins dense que l'eau (0,92 pour l'huile de Colza à 20°C et 1 pour l'eau à 20°C) alors que l'huile est, de façon très nette, plus visqueuse que l'eau. Pour ce qui est des huiles de mécaniques, elles seront classer selon leur viscosité puisque l'huile utilisée dans les moteurs va varier selon les besoin de lubrifications de celui-ci mais aussi selon les température auxquelles l'huile mécanique sera soumise lorsque le moteur sera en marche.
La viscosité dynamique
La viscosité dynamique peut alors être définie en considérant deux couches d'un fluide que l'on nommera abcd et a'b'c'd' en sachant que la couche abcd est animée d'une vitesse relative à a'b'c'd' que l'on notera dv qui sera dirigée selon x. On considère également une force de frottement notée F comme s'exerçant sur la couche a'b'c'd' séparée de dz. Ainsi, la viscosité dynamique, que l'on note η ou µ, est présente au sein de la relation entre la norme de la force de frottement F et le taux de cisaillement dv/dz. On à obtient alors : 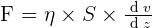 avec S correspondant à la surface de chaque couche de liquide. L'analyse dimensionnelle de la viscosité dynamique donne donc, de façon logique :
avec S correspondant à la surface de chaque couche de liquide. L'analyse dimensionnelle de la viscosité dynamique donne donc, de façon logique : 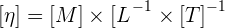 Si on souhaite utiliser les unités du système international d'unité, la viscosité dynamique possède la pascals secondes, noté Pa.s, en unité. Auparavant, on utilisé le poiseuille, noté Pl, qui présentait la même valeur que le pascals secondes. Une ancienne unité du système CGS pour la viscosité dynamique était la poise, notée Po, donc la correspondance était :
Si on souhaite utiliser les unités du système international d'unité, la viscosité dynamique possède la pascals secondes, noté Pa.s, en unité. Auparavant, on utilisé le poiseuille, noté Pl, qui présentait la même valeur que le pascals secondes. Une ancienne unité du système CGS pour la viscosité dynamique était la poise, notée Po, donc la correspondance était : 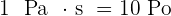 Ainsi, la viscosité de l'eau à 20°C correspond à 1 centipoise, noté cPo, ce qui correspond à 1 mPa.s.
Ainsi, la viscosité de l'eau à 20°C correspond à 1 centipoise, noté cPo, ce qui correspond à 1 mPa.s.
La fluidité
La fluidité correspond à l'inverse de la viscosité dynamique
La viscosité cinématique
Il est possible d'obtenir la viscosité cinématique, noté ν, en divisant la discosité dynamique par la masse volumique, notée ρ, du fluide. On obtient alors la relation suivante :  Son unité, le mètre carré par seconde, noté n².s-1, correspondant, dans l'ancien système CGS comme étant le stokes ou centistokes notés respectivement St et cSt. La conversion est très rapide car :
Son unité, le mètre carré par seconde, noté n².s-1, correspondant, dans l'ancien système CGS comme étant le stokes ou centistokes notés respectivement St et cSt. La conversion est très rapide car : 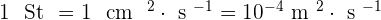 et
et 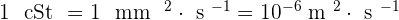
La seconde viscosité
La seconde viscosité correspond au second paramètre scalaire qui permet de caractériser de façon complète un fluide considéré comme étant newtonien. Elle est cependant omise dans la littérature puisque, pour la plupart des fluides usuels, il manque la caractérisation des fluides en ce qui concerne leur approximation newtonienne.
La viscosité de volume
La viscosité de volume correspond à une fonction linéaire des viscosités principale et seconde viscosité. On a ainsi : 
La viscosité élongationnelle
On considère la viscosité élongationnelle comme étant une viscosité qui apparaît lorsqu'une contrainte élongationnelle s'applique au fluide étudié.
Le théorème de Bernoulli : formulation et utilisation

Le théorème de Bernoulli s'applique uniquement à un écoulement incompressible dont la masse volumique reste constante et à un fluide dit parfait dont on néglige les pertes de charge ainsi que les effets visqueux. La quantité de Bernoulli vérifie cette égalité : 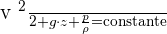 Avec :
Avec :
- v la vitesse du fluide en un point en m/s ;
- g accélération de la pesanteur en N/kg ou m/s² ;
- z l'altitude du point considéré en m ;
- p la pression en un point en Pa ou N/m² ;
- ρ la masse volumique en un point en kg/m³.
Sur une même ligne du courant, la quantité de Bernoulli se conserve et de plus, si l'écoulement est irrotationnel, alors la quantité de Bernoulli se conserve dans tout le fluide.
Applications
Le théorème de Bernoulli a permis l'énonciation d'autres lois et effets :
- La loi de l'hydrostatique ;
- L'effet Magnus ;
- L'effet Venturi ;
- Le Tube de Pitot.
La loi de l'hydrostatique
Quand la vitesse est nulle dans l'équation du théorème de Bernoulli, alors on retrouve la loi de l'hydrostatique.
L'effet Magnus
Si la canalisation a une section constante, et qu'elle ne présente pas d'obstacle, alors la vitesse est constante. Si l'altitude varie, alors l'équation de Bernoulli nous indique que la pression varie à l'opposé de l'altitude.
L'effet Venturi
Si un liquide s'écoule dans une canalisation, alors comme il est incompressible, son débit (volume transitant à travers une surface par unité de temps) est constant. Si la canalisation s'élargit, alors la vitesse diminue (puisque le débit est le produit de la vitesse par la section, les deux varient à l'inverse). Le théorème de Bernoulli nous indique alors que la pression augmente. À l'inverse, si la canalisation se rétrécit, le fluide accélère et sa pression diminue. C'est ce que l'on appelle le tube de Venturi.
Le Tube de Pitot
Le tube de Pitot est une sonde très simple mais essentielle à la sécurité de tous les avions puisqu'elle donne une mesure de la vitesse v de l'air par rapport à l'avion.
Résumer avec l'IA :























Si vous désirez une aide personnalisée, contactez dès maintenant l’un de nos professeurs !
C’est vraiment interressant de voir ça!