Chapitres

L’infiniment grand
Depuis l ‘Antiquité, les hommes ont observé le ciel. Ils se sont intéressés aux étoiles, aux planètes.
Le système Solaire
Le Soleil et l’ensemble des objets en révolution autour de lui constituent le système Solaire.
La terre fait partie du système solaire avec huit autres planètes qui sont :
Mercure, Vénus, la Terre, Mars, Jupiter, Saturne, Uranus, Neptune, "Pluton".
La Terre tourne autour du Soleil sur une orbite quasi circulaire de 150 millions de kilomètres de rayon.
Cette distance est appelée unité astronomique, notée UA.
1 UA = 1,5 x 10 11 m.
Les planètes et leurs satellites, les astéroïdes, les comètes font partie du système Solaire.

Le Système solaire est composé de plusieurs corps , ici classés des plus proches au plus éloignés du centre :
- Le Soleil ;
- 4 planètes telluriques : Mercure, Vénus, la Terre, Mars ;
- Une ceinture d'astéroïdes ;
- 4 planètes géantes :
- Deux géantes de gaz : Jupiter et Saturne ;
- Deux géantes de glace : Uranus et Neptune.
- La ceinture de Kuiper.
Le Système solaire est le système planétaire dans lequel nous vivons et dans lequel se trouve notre Terre. Il est intégré dans la galaxie de la Voie Lactée.
Un système planétaire est un système dans lequel on retrouve des planètes avec des corps inertes tels que des astéroïdes ou des comètes. Le tout gravite autour d'une étoile.
L' adjectif solaire est relatif au Soleil. Le système solaire est donc constitué du Soleil et d ' astres qui orbitent autour de lui tels que des planètes, comètes, astéroïdes, etc. Le système solaire est né il y a environ 4,6 milliards d' années, dans un énorme nuage de gaz et de poussières. Au centre du nuage, une boule lumineuse s' est formée : le Soleil. Des grains de poussières qui tournaient autour du Soleil se sont regroupés pour devenir de grosses boules de tailles différentes: les planètes.
Notre galaxie
Toutes les étoiles que nous voyons à l’œil nu font partie de notre Galaxie.
Elle comporte environ 200 milliards d’étoiles. Elle a la forme d’un disque renflé au centre.
La bande lumineuse, d’apparence laiteuse que l’on observe dans le ciel, est notre Galaxie vue suivant un diamètre de ce disque.
On l’appelle la Voie Lactée.
Notre Galaxie s’étend sur 10 21 m.
À cette échelle, le mètre et l’Unité Astronomique sont des unités mal adaptés.
On utilise l’année de lumière de symbole a.l.
1 a.l = 9,46 x 10 15m
Exemple : Proxima du centaure est l’étoile la plus proche du Soleil.
Elle est située à 40 mille milliards de kilomètres.
Cette grandeur s’exprime avec un nombre plus simple en utilisant l’année de lumière : 4,3 a.l.
L’univers
Il contient des milliards de Galaxies. La Galaxie d’Andromède, qui est la plus proche de la Terre, est située à 2 millions d’années de lumière.
Les Galaxies sont regroupées en amas qui s’éloignent les uns des autres. L’Univers est en expansion.
À l’aide des derniers télescopes, on peut observer l’Univers jusqu’à des distances de 15 milliards d’années de lumière.
L’espace entre les étoiles et les Galaxies est surtout constitué de vide. À l’échelle cosmique, la matière est essentiellement lacunaire.
Comment progresser grâce aux cours de physique en ligne ?
L’infiniment petit
Les atomes : Ils peuvent être assimilés à des sphères dont le rayon atomique est de l’ordre de 0,1 nanomètre (1 nm = 10 –9m).

Un atome est constitué :
D’un noyau central, chargé positivementet d’électrons, chargés négativement en mouvement rapide autour du noyau.
Le noyau est assimilé à une sphère de rayon 100 000 fois plus petit que celui de l’atome.
L’atome est essentiellement fait de vide. Il a une structure lacunaire.
Les molécules : les plus petites molécules ont des dimensions de l’ordre du nanomètre.
Certaines grosses molécules organiques peuvent dépasser le millimètre (1 mm = 10–3m).
L'atome
En 400 av JC, un philosophe grecque nommée Démocrite est le premier homme à penser que la matière est constitué de minuscules particules tellement petite que l'on ne peut les diviser d'où leur nom de atomos qui signifie indivisible en grec.
La première approche des électrons date de l'époque de la Grèce Antique. Ceux-ci avaient pris conscience qu'une certaine oléorésine, l'ambre était capable d'attirée des objets si elle était frottée avec de la fourrure. Sans le savoir, ils venait de découvrir l'électricité statique. Il s'agit du deuxième phénomène électrique dont l'Homme a pris conscience, juste après la foudre.
En 1269, un ingénieur militaire qui servait auprès du prince Charles Premier de Sicile, se mit à étudier le phénomène d'attirance ente des petits objets après qu'ils aient été frottés.
La découvert de l'atome est imputable à Ernest Rutherford. Durant le début des années 1910, il s'est attelé à comprendre la composition de l'atome. Il a alors déterminé que l'atome était constitué d'un noyau qui concentrait toute la charge positive et aussi presque toute la masse de l'atome. Ce noyau est entouré d'un nuage électronique composé d'électrons.
L'un de ses collègues de laboratoire, Niels Bohr, a quant à lui démontré que les états de l'électrons dépendaient de l'énergie déterminée par le nombre n de l'atome. C'est à lui qu'on doit la compréhension de l'émission d'un photon lors d'un passage à un état inférieur.
La masse des électrons est négligeable devant celle du noyau.
On dit que la masse d'un atome est concentrée dans son noyau
La charge électrique d'un atome est la somme de la charge électrique + des particules du noyau et celle – des électrons.
Cette somme est nulle : On dit que l'atome est électriquement neutre.
Les charges électriques étant les même, il y a autant d'électrons qui gravitent autour du noyau que de particules le constituant.
Exemple : L'atome de fer a 26 électrons et 26 particules + dans son noyau.
La taille d'un atome est infiniment petite.
Le diamètre d'un atome vaut en moyenne 10-1nm ( 1nm = 10 -9 m ).
Le diamètre du noyau vaut en moyenne 10-6 nm.
Le noyau est 100 000 fois plus petit que l'atome.
Entre les électrons et le noyau, il n'y a que du vide... Beaucoup de vide !
On parle de la structure lacunaire de l'atome.
Les Ions
La formation d'ions
Un ion est un atome, qui à perdu ou gagné un ou plusieurs électrons (3 max). Exemple, le lithium (Li) perd un électron il devient l'ion de lithium (Li+ ). Un autre exemple, le fluor (F) gagne un électron, il devient l'ion de fluor (F- ). Si un atome perd 2 électrons, imaginons que cette atome soit l'hydrogène (H), il devient l'ion d'hydrogène (H +2 ).
Définitions

Un atome (ou groupe d'atomes) qui perd un ou plusieurs électrons devient une espèce chimiquement chargée appelée ion. La charge du noyau reste inchangée.
Un ion négatif est un atome (ou groupe d'atome) qui à gagné un ou plusieurs électrons.
Un ion positif est un atome (ou groupe d'atome) qui à perdu un ou plusieurs électrons.
Les électrons
L'électron est donc l'un des composants de l'atome au même titre que les neutrons et protons. C'est une particule élémentaire que l'on note petit e et dont la charge élémentaire est de signe négatif. Ils s'organisent autour du noyau de l'atome dans ce que l'on appelle un nuage électronique.
Les électrons et leurs propriétés ont aidé à la compréhension d'une multitude de phénomènes physiques, notamment en termes de conductivité.
Des outils de description de l’Univers.
Les puissances de 10
En Sciences Physiques, un nombre est souvent écrit sous la forme a x 10 n ou a . 10 n: appelée notation scientifique ou écriture scientifique.
Complément : a est un nombre décimal tel que :
1 £ a £ 10
n est un nombre entier relatif : n Î Z.
Exemples :
- Distance Terre – Soleil : 150 millions de kilomètres 150 x 10 6 = 1,50 x 10 8
- Taille d’une bactérie un millième de mm : 1 / 1000 mm ou 10–3 x 10–3= 10–6 m
Formules :
Opérations
10n x 10m = 10n+m
(10n)m = 10n.m
Multiples et sous multiples d’une unité
| Facteur multiplicatif | Préfixe | Symbole | Etymologie |
|---|---|---|---|
| 10-18 | Atto | a | Danois : atten : dix-huit |
| 10-15 | Femto | f | Danois : femten : quinze |
| 10-12 | Pico | p | Italien : picolo : petit |
| 10-9 | Nano | n | Latin : nanus : nain |
| 10-6 | Micro | µ | Grec : mikros : petit |
| 10-3 | Milli | m | Latin : mille : millième |
| 1 | Unité | ||
| 103 | Kilo | k | Grec : khilioi : mille |
| 106 | Méga | M | Grec : mégas : grand |
| 109 | Giga | G | Grec : gigas : géant |
| 1012 | Téra | T | Grec : téras : monstre |
| 1015 | Peta | P | Grec : pente : cinq (mille à la puissance 5) |
| 1018 | Exa | E | Grec : hex : six (mille à la puissance 6) |
Exemples : le kilomètre : km ; le kilowatt : kW ; le millimètre : mm.
Comparaison de longueurs et ordre de grandeur.
Comparaison de longueurs
On donne : l’épaisseur d’une feuille d’or e1 = 7 mm et on donne l’épaisseur d’un cheveu : e2 = 0,06 mm.
Quelle est la longueur la plus grande ?
N Pour comparer deux longueurs, il faut les exprimer à l’aide du même multiple ou sous-multiple du mètre.
Dans le cas qui nous intéresse, on peut utiliser le m comme sous-multiple.
e1 = 7 mm et e2 = 0,06 x 10 3 = 60 mm, en conséquence e1 < e2.
Ordre de grandeur
L’ordre de grandeur d’un nombre très grand ou très petit est la puissance de 10 la plus proche de ce nombre.
Exemple 1 :
L’atome de Germanium est représenté par une sphère de rayon Ra = 123 pm et son noyau a un rayon Rn = 4,99 fm.
On dit que les longueurs de deux objets sont du même ordre de grandeur si le rapport de la longueur du plus grand sur la longueur du plus petit est voisin de 1.
La connaissance de l’ordre de grandeur permet de comparer rapidement les grandeurs étudiées.
L’ordre de grandeur constitue un outil d’approximation fondamental dans le travail du physicien.
Il peut savoir tout de suite s’il peut négliger une grandeur devant une autre et simplifier le problème posé.
L’ordre de grandeur est un outil de contrôle permanent. Il permet d’éviter les erreurs grossières.
Donner un ordre de grandeur du rapport entre le rayon de l’atome et celui du noyau.
Ordre de grandeur du rapport :
En conséquence, le rayon de l’atome est environ 20 mille fois plus grand que celui du noyau.
On dit que la taille de l’atome est très grande devant celle du noyau.
Combien d’atomes de Germanium faut-il aligner pour obtenir une longueur de 1 mm ?
Nombre d’atomes de Germanium nécessaires.
Il faut aligner environ 4 millions d’atomes de Germanium.
Exemples 2 :
Le nombre de secondes dans une année est-il de l’ordre :
- De la dizaine de milliards ?
- De la dizaine de millions ?
- Ou de la dizaine de milliers ? Justifier la réponse.
Nombre de seconde dans une année :
N = 365,25 x 24 x 3600
N» 400
Quelques exercices
Exercice 1 : Des atomes froids pour mesurer le temps

Les horloges à fontaine atomique de césium sont des horloges parmi les plus précises à ce jour. Elles utilisent une radiation dont la fréquence correspond à la transition hyperfine entre deux niveaux d’énergie atomique de l’atome de césium. Quand les atomes sont « lents » ou « froids », on peut mesurer avec grande précision la fréquence correspondant à cette transition d‘énergie atomique. La précision et la stabilité des horloges atomiques sont telles qu’elles constituent aujourd'hui les étalons de temps. Une horloge de ce type, construite à l’observatoire de Paris, atteint une précision relative de 10–15.
Dans cet exercice, on s’intéresse au principe de fonctionnement d’une horloge à fontaine atomique.
Dans une enceinte sous vide, un nuage d’atomes de césium est d’abord piégé et refroidi a quelques microkelvins dans un piège magnéto-optique (PMO) à l’aide de six faisceaux laser (figure 1) ; ainsi le nuage d’atomes ne s’éparpille pas trop vite sous l’effet de l'agitation thermique.
Après extinction des faisceaux laser, le nuage est lancé vers le haut (figure 2). Les atomes de césium passent alors dans une cavité à micro-ondes où ils interagissent avec une radiation électromagnétique.
Puis ils poursuivent leur mouvement vers le haut en ralentissant sous l’effet de la pesanteur et retombent en traversant une deuxième fois la cavité à micro-ondes.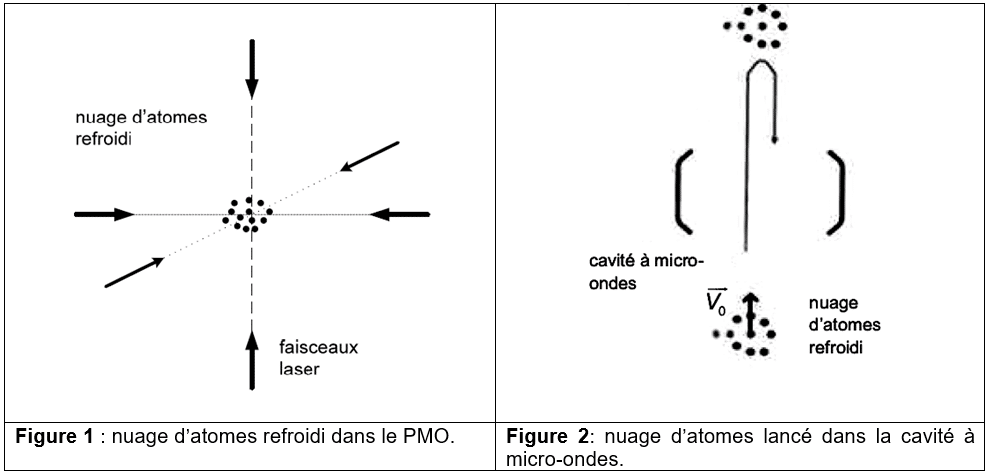
La précision de ce type d‘horloge est d’autant plus grande que le temps séparant les deux passages par la cavité à micro-ondes est grand.
Avec une fontaine haute de un mètre, ce temps est de l’ordre de la seconde, ce qui est cent fois plus qu‘avec un jet atomique conventionnel.
Données :
- Constante de Planck : h = 6,63 x 10–34s ;
- Accélération de la pesanteur terrestre : g = 9,8 m.s–2 ;
- Masse d‘un atome de césium : M = 2,207 x 10–25 kg ;
- Longueur d’onde du rayonnement émis par chaque laser : l = 852 nm ;
- Fréquence de la transition hyperfine de l’atome de césium : 9193 MHz ;
- Domaines du spectre électromagnétique en fonction de la longueur d’onde :

1. Quelques principes mis en œuvre dans le refroidissement d’un nuage d’atomes
1.1. Interaction laser - atome de césium au repos
On s’intéresse à un atome initialement immobile dans le référentiel du laboratoire. La quantité de mouvement du système {atome + photon} se conserve. Après absorption d’un photon de quantité de mouvement [ p = \frac {h} {lambda} ] (figure 3.a), l'atome est animé d’une vitesse de « recul » , de même direction et de même sens que le photon incident (figure 3.b).

Dans la situation décrite par les figures 3.a et 3.b, montrer que la valeur de la vitesse de « recul » Vrec dans le référentiel du laboratoire, a pour expression : [ V_{rec} = \frac {h} {lambda M} ]
avec h la constante de Planck, l la longueur d’onde du laser, et M la masse de l'atome de césium. Calculer la valeur de la vitesse Vrec.
1.2. Interaction laser - atome de césium en mouvement dans le référentiel du laboratoire
On restreint l’étude au cas particulier où l’atome de césium est en mouvement dans le référentiel du laboratoire décrit par la figure 4.

La conservation de la quantité de mouvement pour le système {atome+photon} permet d‘écrire la relation : [ \frac {h} {lambda} = - M V = -M V' ]
avec V et V ’ les vitesses de l'atome respectivement avant et après absorption d‘un photon.
1.2.1. Interpréter cette relation en justifiant chacun de ses termes et de ses signes.
Exprimer V ’ en fonction de V et de Vrec et conclure dans ce cas sur l’effet produit par l’absorption d’un photon sur la vitesse de l’atome de césium.
L’absorption d’un photon se fait sur une durée de l’ordre de Dt = 30 ns pour l’atome de césium.
1.2.2. Calculer l’ordre de grandeur de l’accélération subie par cet atome lors de l’absorption d'un photon. Le comparer à l’accélération de cet atome en chute libre.
1.3. Le piège magnéto-optique (PMO)
Dans le PMO, les six faisceaux laser sont disposés par paire selon trois directions orthogonales de |’espace.
Par paire, selon une direction, ils se propagent dans des sens opposes (figure 1).
On considère un atome de césium de vitesse dans le référentiel du laboratoire en interaction avec une paire de faisceaux laser de fréquence n. On se place dans le cas où l’atome de césium se rapproche du laser de gauche, tandis qu’il s'éloigne du laser de droite comme illustré sur la figure 5.

Dans le référentiel lié à l’atome, les fréquences des deux faisceaux laser perçues par l'atome de césium sont différentes.
1.3.1. Quel est le phénomène mis en jeu ? Comparer chacune des deux fréquences perçues par rapport à la fréquence n.
1.3.2. Pour obtenir un ralentissement de l’atome de césium dans la situation de la figure 5, indiquer le photon (gauche ou droite) qui doit être absorbé par l’atome en mouvement.
Les atomes de césium sont ralentis au centre de six faisceaux laser. On définit la fréquence de résonance atomique par [ nu_{12} = \frac{E_{2} - E_{1}} {h} ]
où E1 et E2 sont les énergies des deux niveaux d’énergie de l’atome de césium mis en jeu. La probabilité pour un atome de césium d‘absorber un photon d'un faisceau laser est d’autant plus grande que la fréquence du faisceau perçue par l’atome est proche de la fréquence de résonance atomique.
1.3.3. Parmi les propositions ci-dessous choisir celle qui convient et la justifier.
Pour obtenir un ralentissement efficace des atomes de césium, la fréquence n des lasers est réglée de sorte que :
- n est égale à n12.
- n est légèrement inférieure à n12.
- n est légèrement supérieure à n12.
Principe de la fontaine de césium
Lorsqu’un atome de césium passe dans la cavité à micro-ondes, il est excité par le rayonnement produit dans la cavité. Ce rayonnement a la même fréquence que celle associée à la transition hyperfine de l’atome de césium.
2.1. Justifier le terme « micro-ondes » attribué à la cavité.
On suppose qu’à l’instant t = 0, le nuage atomique dans l’enceinte sous vide est à l’altitude z = 0. Il est lancé vers le haut avec une vitesse initiale V0 = 5,0 m.s-1 (figure 6).
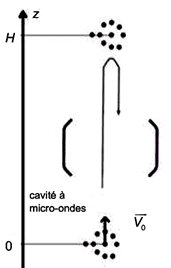
2.2. Montrer que la date tmax à laquelle le nuage d’atomes atteint le sommet de la fontaine a pour expression : [ t _ { text {max} } = \frac {V _ {0}} {g}] . En déduire l‘expression de la hauteur H de la fontaine : [ H = \frac {V _ {0}^{2}} {2g}].
2.3. Calculer les valeurs de tmax et de H puis vérifier la cohérence de ces valeurs avec le texte introductif.
2.4. Des expériences de refroidissement ont été conduites en 1992 par les physiciens de l’ENS (École normale supérieure) en collaboration avec le CNES (Centre national d’études spatiales), lors d’une série de vols paraboliques en avion permettant de se placer dans les conditions de gravité réduite. Dans quel but ces expériences ont-elles été menées ? Justifier votre réponse.





















Si vous désirez une aide personnalisée, contactez dès maintenant l’un de nos professeurs !