Chapitres
- 01. Le poids, unité de mesure internationale
- 02. La pesanteur : intensité et réalité ?
- 03. Déterminer le poids d’un objet ?
- 04. Relation entre le poids et la gravitation ?
- 05. Définir le champ de gravitation ?
- 06. Applications concrètes ⚡️
- 07. Les lois physiques qui s'appliquent à la gravitation ainsi qu'au champ gravitationnel ??
? Le poids et la gravitation sont deux concepts étroitement liés mais distincts en physique.
- Le poids désigne la force exercée sur un objet en raison de la gravité
- La gravitation est l'interaction mutuelle d'attraction entre les objets massifs
Le poids dépend de la masse de l'objet et de l'intensité de la gravité
La gravitation suit la loi universelle de Newton
Bien qu'ils partagent une relation avec la masse et influencent les mouvements des objets, le poids est une mesure spécifique liée à la Terre, tandis que la gravitation est une force fondamentale qui régit l'ensemble de l'univers.
? Comprendre ces différences et points communs est essentiel pour approfondir notre compréhension de la physique et de l'astronomie.

Le poids, unité de mesure internationale

⚠️ Poids et masse sont deux choses différentes et souvent confondues
Un objet A sphérique possédant une masse mA (comme une planète par exemple) va créer autour de lui un champ de gravitation.
Si on place un second objet B possédant une masse mB à proximité de l’objet B, donc dans le champ de gravitation, une force va s’exercer sur l’objet B, l’entrainant vers le centre de l’objet A.
? C’est la force gravitationnelle
Dans le cas où l’objet B se trouve très proche de l’astre (pratiquement à la surface), cette force est assimilable au poids.
Le poids, noté P, correspond à la force de gravitation exercée par une planète ou un astre sur tout corps se trouvant à proximité de sa surface et possédant une masse.
La valeur du poids dépend de la pesanteur et de la masse. Sa direction est verticale, et elle est dirigée vers le bas.
? Sur Terre (et sur la majeure partie des astres), elle sera dirigée vers le centre de la Terre
Le poids est une force exprimée en newtons (N). Le poids d’un objet est lié à sa masse.
La masse est une grandeur positive liée à la quantité de matière contenue dans un objet. Son unité, dans le système international, est le kilogramme (kg).
? La masse est égale à la masse des atomes et particules contenues dans l’objet, et sera identique quel que soit l’endroit de l’univers où cette masse sera mesurée.
On note : 
Lorsque l’on mesure la masse d’un objet ou d’une personne, on parle souvent d’une « pesée », mot dérivant de « poids »
Or, c’est un abus de langage. En effet, les balances classiques ne mesurent pas le poids de l’objet, mais sa masse. Il est donc très important de distinguer le poids d’un objet, qui correspond à la force d’attraction exercée par l’astre sur lequel il se trouve (et qui varie selon l’astre et l’altitude), et sa masse, invariante selon ces mêmes conditions.
? Dans les textes scientifiques et les exercices notamment, on prendra soin de prêter attention au contexte d’utilisation du mot « poids », qui n’aura pas la même signification selon qu’il soit utilisé par un particulier (utilisant le langage courant) ou par un scientifique ou professeur.
La pesanteur : intensité et réalité ?

? L’intensité de pesanteur, notée g, est une force attractive dirigée vers le sol verticalement, ayant pour unité le N.kg-1
On peut également l’exprimer en m.s-2, en référence au champ d’accélération de la pesanteur. Elle s’exerce sur tout corps possédant une masse à proximité d’un astre ou planète. Sa valeur est dépendante de l’altitude et de la planète sur laquelle l’objet se trouve.
?️ La pesanteur a été, pendant un temps, mesurée à l’aide d’un pendule. Galilée s’est intéressé à la période des pendules au XVIIe siècle, et a émis l’hypothèse que cette dernière était uniquement dépendante de la longueur du pendule.
Quelques années plus tard, Huygens complète cette hypothèse en prouvant que cette période est également dépendante d’un paramètre terrestre, qu’il appelle g : la pesanteur.
? Il parvient alors à mesurer cette pesanteur à Paris, avec une valeur estimée à 9,812 m.s-2
Il est cependant nécessaire de prendre en compte l’aspect général de la Terre, ainsi que le lieu de mesure, lorsque l’on tente de mesurer la pesanteur. En effet, la Terre n’étant pas une sphère homogène et fixe (à cause de sa rotation autour du Soleil et sur elle-même), la pesanteur sera différente à différents points de sa surface.
? La pesanteur est donc dépendante de la rotation terrestre, de l’altitude, mais également de paramètres plus surprenants comme les écarts de densité du sous-sol ou la force des marées. Sur Terre, au niveau de la mer (soit à une altitude de 0 m), g a une valeur de 9,80665 N.kg-1.
Déterminer le poids d’un objet ?

Par un calcul simple
Si un objet possède une masse m, alors son poids P peut être calculé grâce à la relation suivante :

Dans cette formule, les unités sont les suivantes :
- m est en kilogramme (kg)
- P est en newton (N)
- g est en newton par kilogramme (N.kg-1)
Bien que la masse soit invariable quel que soit le système d’étude, le poids est variable car la valeur de la pesanteur est variable.
En effet, cette valeur est dépendante de l’astre à proximité de l’objet étudié, ainsi que de l’altitude à laquelle se trouve cet objet par rapport à l’astre.
? Par exemple, un objet ayant une masse égale à 1 kg n’aura pas le même poids à la surface de la Lune ou à la surface de la Terre. En effet, la pesanteur est beaucoup plus faible sur la Lune que sur la Terre : sa valeur est d’environ 1,6 N.kg-1 sur la Lune, alors qu’elle est de 9,8 N.kg-1 sur la Terre.
❌ Une telle différence (la pesanteur lunaire étant pratiquement 6 fois inférieure à la pesanteur terrestre) s’explique par le fait que la masse et le rayon lunaire sont fortement inférieurs à la masse et le rayon terrestre
C’est ce phénomène qui permet d’expliquer les images des astronautes « flottant » au-dessus du sol lunaire : la force nécessaire pour s’élever du sol est faible car la force « ré-attirant » l’astronaute vers le sol (son poids) l’est également.
Par une mesure ou une machine

Le poids peut être mesuré à l’aide d’un dynamomètre. Ce système est, dans sa version simplifiée, basé sur un ressort dont la raideur est connue.
Le poids sera alors calculé selon une formule simple de type « force = raideur x allongement », qui découle de la loi de Hooke.
Relation entre le poids et la gravitation ?

D'après la loi de la gravitation, la force s'exerçant entre deux corps A et B de masse mA et mB, dont les centres de gravité sont séparés par une distance d, vaut : 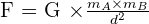
On rappelle que G est la constante de gravitation, calculée comme la force entre deux masses d’un kilogramme chacune, séparée par une distance d’un mètre.
✅ Elle est toujours égale à G = 6,67 x 10-11 N.m2.kg-2, quel que soit l’altitude ou l’astre sur lequel on se trouve.
- Si un corps B est situé à proximité de la surface terrestre, qui correspond au corps A, alors la distance entre le centre de la Terre et ce corps correspond au rayon terrestre rT, qui est égal à 6371 km
- Si le corps A correspond à la Terre, alors mA correspond à la masse de la Terre mT, qui est égale à 5,97 x 1024 kg. On note alors la masse du corps B simplement m
- Dans ces conditions, la valeur de la force de gravitation calculée correspond au poids p de l'objet : il y a alors équivalence entre la loi de gravitation et l’expression du poids
- Le poids correspond donc à la force gravitationnelle exercée par la Terre sur l’objet
- La relation devient alors :

- Si, au contraire, l’objet se trouve à une altitude h par rapport au niveau de la mer, la relation devient alors :
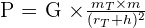
- Cela nous permet donc d’affirmer que le poids est dépendant de l’altitude à laquelle se trouve l’objet
Valeur de l’intensité de la pesanteur
Si l'on compare cette relation à celle que l'on utilise d'habitude pour exprimer le poids, alors on peut en tirer une expression de l'intensité de la pesanteur :
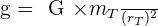
On peut donc calculer l'intensité de la pesanteur terrestre :
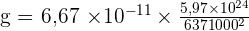 g = 9,81 N.kg-1
g = 9,81 N.kg-1
On retrouve donc bien la valeur moyenne généralement admise pour l'intensité de la pesanteur terrestre. Cette valeur est valable lorsque l’altitude de l’objet est négligeable par rapport au rayon de la Terre.
Définir le champ de gravitation ?
En physique classique, on appelle champ gravitationnel, ou encore champ de gravitation, un champ qui est réparti dans l'espace et dû à la présence d'une masse qui est alors susceptible d'exercer une influence gravitationnelle sur tous les autres corps pouvant être présent à proximité immédiate ou non.
On peut démontrer que le champ gravitationnel créé en un point quelconque par un corps ponctuel dérive d'un potentiel scalaire dit newtonien.

L'introduction de cette grandeur permet de s'affranchir du problème de la médiation de l'action à distance apparaissant dans l'expression de la force de gravitation universelle.
⏳ On peut interpréter le champ gravitationnel comme étant la modification de la métrique de l'espace-temps
L'approximation newtonienne est alors valable uniquement dans le cas où les corps présentent une vitesse faible par rapport à celle de la lumière dans le vide et si le potentiel gravitationnel qu'ils créent est tel que le quotient du potentiel gravitationnel sur le carré de la vitesse de la lumière dans le vide est négligeable.
On peut approcher le champ électrique et le champ gravitationnel.
En effet, l'expression du champ et du potentiel ne sont différents que d'une constante. De plus, les principaux théorèmes de calculs, celui de la superposition ou de Gauss par exemple, peuvent s'appliquer dans les deux cas. Ce qui les différencie alors est le caractère attractif, donc entre deux charges de signe opposé, ou répulsif, donc entre deux charges de même signe, du champ électrique tandis que le champ gravitationnel ne peut être qu'attractif.
Le principe de l'analogie
- L'analogie repose sur la similitude des lois de Coulomb (électromagnétisme) et loi de Newton (gravitation)
- Il est souvent inutile de faire les calculs de champs gravitationnels à partir de répartitions de masses, on procède plutôt par analogie avec les résultats connus de l'électrostatique
- La force d'interaction gravitationnelle, tout comme la force d'interaction électrostatique, est une force conservative. Ainsi, elles représentent toutes les deux le gradient d'une énergie potentielle
- Dans ce cas, il est alors possible d'adapter absolument tous les calculs de champ et de potentiel étudiés dans le cadre du cours sur la distribution de masses dans le but de calculer le champ et le potentiel gravitationnels en un point défini de l'espace. Il en va de même avec le théorème de Gauss
Il peut être intéressant de mentionner que la force électrique fondamentale, également appelée force de Coulomb, peut être utilisée comme fondement de l'électrostatique. Ainsi, on peut déduire de ce fondement le théorème de Gauss.
? C'est donc pour cela que l'on peut dire que la ressemblance formelle, c'est-à-dire les similarités des formules mathématiques, entre la force de Coulomb et la force gravitationnelle est une base solide permettant de fonder l'analogie entre les deux classes de phénomènes énoncés dans ce cours.
Ainsi, à partir de la force de Coulomb et par superposition, on peut être capable d'établir des expressions intégrales du champ électrique en fonction de la distribution de charge. Bien que ces calculs soient trop complexes pour être utiles dans les calculs analytiques, ils peuvent être très utiles afin de déterminer un champ électrique par résolution numérique, c'est-à-dire par ordinateur.
? Notons qu'il est possible de démontrer ces formules en utilisant le théorème de superposition.
Applications concrètes ⚡️

Le champ électrique
? En physique, on appelle champ électrique tout champ vectoriel créé par des particules électriquement chargées. Plus exactement, lorsque nous sommes en présence d'une particule chargée, les propriétés locales de l'espace défini sont alors modifiés, ce qui permet de définir la notion de champ.
En effet, si une autre charge se trouve être dans le dit champ, elle subira ce qu'on appelle l'action de la force électrique qui est exercée par la particule malgré la distance. On dit alors du champ électrique qu'il est le médiateur de ladite action à distance.
Si on se veut plus précis, on peut définir dans un référentiel galiléen défini, une charge q définie de vecteur vitesse v qui subit de la part des autres charges présentes, qu'elles soient fixes ou mobiles, une force qu'on définira de force de Lorentz.
Cette force se décompose ainsi :
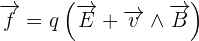 avec :
avec :
 le champ électrique. Celui-ci décrit dans ce cas la partie de la force de Lorentz qui est indépendante de la vitesse de la charge
le champ électrique. Celui-ci décrit dans ce cas la partie de la force de Lorentz qui est indépendante de la vitesse de la charge le champ magnétique. Celui-ci décrit ainsi la partie de la force exercée sur la charge qui dépend du déplacements de cette même charge dans le référentiel choisi.
le champ magnétique. Celui-ci décrit ainsi la partie de la force exercée sur la charge qui dépend du déplacements de cette même charge dans le référentiel choisi.
⚡️ De plus, il est important de noter que les deux champs, électrique et magnétique, dépendent du référentiel d'étude :
- Avec cette formule, on peut alors définir le champ électrique comme étant le champ traduisant l'action à distance subie par une charge électrique fixe dans un référentiel défini de la part de toutes les autres charges, qu'elles soient mobiles ou fixes.
- Mais on peut également définir le champ électrique comme étant toute région de l'espace dans laquelle une charge est soumise à une force dite de Coulomb. On commence à parler de champ électrostatique lorsque, dans un référentiel d'étude, les charges sont fixes.
- Notons d'ailleurs que le champ électrostatique ne correspond pas au champ électrique comme décrit plus haut dans cet article puisqu'en effet, lorsque les charges sont en mouvement dans un référentiel, il faut ajouter à ce référentiel un champ électrique qui est induit par les déplacement des charges afin d'obtenir un champ électrique complet.
Mais, le champ électrique reste dans la réalité un caractère relatif puisqu'il ne peut exister indépendamment du champ magnétique. En effet, si on observe la description correcte d'un champ électromagnétique, celui-ci fait intervenir un tenseur quadridimensionnel de champ électromagnétique dont les composantes temporelles correspondent alors à celle d'un champ électrique. Seul ce tenseur possède un sens physique. Alors, dans le cas d'un changement de référentiel, il est tout à fait possible de transformer un champ magnétique en champ électrique et inversement.
Le champ électrostatique
?? On parle de champ électrostatique lors que les charges qui constitue le champ sont au repos dans le référentiel d'étude. Ce champ est donc déduit de l'expression de la loi de Coulomb, aussi appelée interaction électrostatique. En physique, on appelle champ électromagnétique la représentation dans l'espace d'une force électromagnétique exercée par des particules chargées. Ce champ représente alors l'ensemble des composantes de la force électromagnétique qui s'appliquent à une particule chargée qui se déplace alors dans un référentiel galiléen.
On peut alors définir la force subie par une particule de charge q et de vecteur vitesse par l'expression suivante :
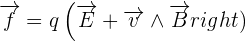
Avec :
 le champ électrique. Celui-ci décrit dans ce cas la partie de la force de Lorentz qui est indépendante de la vitesse de la charge
le champ électrique. Celui-ci décrit dans ce cas la partie de la force de Lorentz qui est indépendante de la vitesse de la charge le champ magnétique.
le champ magnétique.
? Celui-ci décrit ainsi la partie de la force exercée sur la charge qui dépend du déplacement de cette même charge dans le référentiel choisi :
- En effet la séparation de la partie magnétique et de la partie électrique de dépend que du point de vue pris selon le référentiel d'étude
- De plus, il peut être intéressant de savoir que les équations de Maxwell régissent les deux composantes couplées, c'est à dire électrique et magnétique, de sorte que toute variation d'une composante induira la variation de l'autre composante
D'ailleurs, le comportement des champs électromagnétiques se trouve décrit de façon classique par les équations de Maxwell et de manière plus générale par l'électrodynamique quantique. La façon la plus utilisée afin de définir le champ électromagnétique est celle du tenseur électromagnétique de la relativité restreinte.
Les lois physiques qui s'appliquent à la gravitation ainsi qu'au champ gravitationnel ??

Le théorème de Gauss
Le théorème de Gauss permet, en électromagnétisme, de calculer le flux d'un champ électrique à travers une surface qui est fermée et ce grâce à la connaissance des charges électriques que cette surface renferme. Il s'énonce ainsi :
Le flux du champ électrique à travers une surface S fermée est égal à la somme des charges électriques contenues dans le volume V délimité par cette surface, divisée par la permittivité du vide.
Loi de Coulomb
⚖️ Coulomb, un physicien français, a établi en 1758 que le champ doit varier comme le carré inverse de la distance entre les charges à une précision de 0,02 sur l'exposant avec l'aide d'un dispositif appelé balance de Coulomb. Cette balance est constituée d'un fil de torsion en argent sur lequel est fixé des matériaux chargés.
Ainsi, la loi d'attraction entre deux charges ponctuelles notées q1 et q2 , fixes dans le référentiel défini et séparées par une distance r, se définit ainsi :
- La force est dirigée selon la droite reliant les deux charges ;
- Elle est attractive si les charges sont de signes opposés et répulsifs sinon ;
- Son intensité est proportionnelle aux valeurs de q1 et q2 et varie en raison inverse du carré de la distance r.
Il est alors possible de traduire ces caractéristiques en une formule exprimant la force exercée par q1 sur q2 :
 avec :
avec :
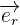 le vecteur unitaire de la droite reliant q1 et q2 qui est dirigée dans le sens 1 vers 2
le vecteur unitaire de la droite reliant q1 et q2 qui est dirigée dans le sens 1 vers 2 la permittivité diélectrique du vide
la permittivité diélectrique du vide
? Ce qui peut rendre la compréhension de cette formule compliquée est la notion de force à distance
En effet, comment une charge peut savoir qu'une autre charge ponctuelle se trouve à une certaine distance d'elle et alors exercer sur force sur cette charge en fonction de la distance qui les sépare. Dans ce cas, tout comme pour un champ gravitationnel, il peut être utile de séparer dans la loi de force ce qui dépend de la charge subissant la force et donc d'obtenir la relation suivante :
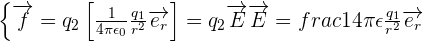 avec :
avec :
 un champ électrique électrostatique créé à partie de la charge q1 au point où se trouve la seconde charge q2
un champ électrique électrostatique créé à partie de la charge q1 au point où se trouve la seconde charge q2
Ainsi, avec cette relation, il est plus aisé d'interpréter l’existence d'une force à distance :
- En effet, la charge considérée comme "source", c'est-à-dire q1, crée en tout point de l'espace un champ électrique dont la forme est donnée par la relation exprimée ci-dessus, et une charge quelconque considérée comme "test" subira l'effet de ce champ sous la forme d'une force égale au produit de cette charge par le champ électrostatique
- Dans ce cas, ce champ électrostatique apparaîtra comme la force entre deux particules ponctuelles fixes par unité de charge.
Principe de superposition
Il est possible d'appliquer le principe de superposition à un système de type entrée-sortie si :
- La somme de deux entrées quelconque correspond à la somme des deux sorties correspondantes ;
- Un multiple d'une entrée quelconque correspond le même multiple de la sortie correspondante.
Dans ce cas, c'est-à-dire celui d'un système physique, on peut appeler l'entrée excitation et la sortie réponse. On obtient alors, en notant les excitations ƒ et les réponses x (donc les mouvements générés par les forces mécaniques ƒ) :
- Lorsque l'on sollicite le système par une entrée, donc une excitation notée ƒ1, une réponse, donc un déplacement, qui sera noté x1 ;
- Lorsque l'on sollicite le système par une entrée, donc une excitation notée ƒ2, une réponse, donc un déplacement, qui sera noté x2 .





















Si vous désirez une aide personnalisée, contactez dès maintenant l’un de nos professeurs !
Sachant que l’intensité de pesanteur sur terre est d’environ 10/m2 , calculer la valeur de la masse d’un dynamomètre 2 N merci
Bonjour Pagès, avez-vous essayé de contacter l’un de nos professeurs pour recevoir une aide personnalisée ? Excellente journée ! 🙂
mon moteur TOURNE par gravitation apres quelques tours il deviens AUTONOME il est dans ma cave on peut le voir
J’aimerais en savoir plus si possible
Bonjour,
Pour une aide personnalisée, vous pouvez contacter nos professeurs :)
Si la Constante gravitationnelle est identique peu importe la planète je ne comprends pas pourquoi une même masse est différente en poids sur 2 planètes ? Merci d’ avance pour votre aide.
bonjour . Comment varie l’intensité du corps lorsque celui-ci s’éloigne de la terre?
montrer que l’intensite gravitationnelle d’une planete ne depent que de son rayon de sa masse volumique