Chapitres

La puissance : une notion physique à étudier

La puissance, en physique, permet d'indiquer la vitesse à laquelle un travail est fourni. Cela correspond alors à la quantité d'énergie par unité de temps fournie par un système à un autre système. On peut donc conclure que la puissance correspond à une grandeur scalaire et à un débit d'énergie. Ainsi, si deux systèmes de puissances différentes fournissent le même travail, et donc la même énergie, ce sera le plus puissant des deux systèmes qui sera donc le plus rapide. On peut exprimer la capacité d'un système à fournir un travail en un temps donné à l'aide du rapport suivant : [ P = \frac { W } { t } ] On peut déduire de cette formule, que l'intégrale de la puissance fournie par rapport au temps représente alors le travail fourni par le système. En ce qui concerne la notation est les unités, dans le SIU, le système international d'unité, une puissance s'exprime en watts, en joules par seconde ou encore en kg.m2.s-3. Autrefois, on utilisait encore le cheval-vapeur. Cette unité comparait alors la traction d'une machine à vapeur à celle d'un cheval de trait.
La puissance correspond à une variable d'effort
En général, on considère la puissance comme étant le produit d'une variable d'effort -qui peut correspondre à une force, un couple, une pression ou encore à une tension- qui est alors nécessaire à la mise en mouvement contre la résistance exercé par le système, par une variable de flux -qui peut correspondre à une vitesse, une vitesse angulaire, un débit ou encore à l'intensité du courant- qui sera entretenue malgré l'existence de cette résistance. Afin d'illustrer ce propos, on peut prendre l'exemple de la puissance nécessaire afin d'imposer un déplacement à un véhicule. En effet, cette puissance correspond alors au produit de la force de traction exercée par la vitesse de déplacement. De ce fait, la puissance d'un moteur rotatif correspond au produit du couple qu'il transmet au travers de la vitesse de rotation qu'il est capable d'entretenir malgré la résistance. Autre exemple, l'ampoule électrique est capable de convertir l'énergie électrique en lumière et en chaleur. Ainsi, la puissance consommée correspond au produit de la tension électrique par l'intensité du courant qui traverse cette ampoule. On peut définir la puissance moyenne Pm avec le quotient l'énergie E par la durée τ de ce phénomène : [ P_m = \frac { E } { tau } ] La puissance instantanée correspond quant à elle à la dérivée de l'énergie fournie par rapport au temps : [ P_m = \frac{ text { d } E } { text { d } tau } ] On obtient donc : [ P_m = \frac{ 1 } { tau } int _ { 0 }^{ tau } P left( t right) d t].
Le cas de la puissance électrique

La puissance électrique, très souvent notée P, possède pour unité le watt, de symbole W. Elle correspond au produit de la tension électrique, donc en volts, aux bornes de laquelle on branche l'appareil avec l'intensité du courant électrique, donc en ampères, qui va donc traverser l'appareil. Notez que ceci est vrai pour les appareils qui sont purement résistifs.
La puissance au sein d'un régime continu
Lorsque la tension et le courant sont continu, on définit la puissance avec la formule suivante : [ P = U times I ] Avec U et I des valeurs constantes de la tension aux bornes du dipôle et de l'intensité du courant à travers le dipôle. Notons que si l'on considère R comme étant la résistance du dipôle, on a : [ U = R times I ] On obtient donc en définitive la formule de calcul de la puissance suivante : [ P = R times I ^ 2 = \frac { U ^ 2 } { R } ] Il est possible de modéliser un dipôle actif linéaire, donc un électromoteur, avec un modèle équivalent de Thévenin même si ce modèle, très sommaire, ne permet pas de rendre compte des éventuelles chutes de tension en charge ou encore des puissances électriques mises en jeu dans un domaine de validité qu'il faut nécessairement préciser. Ainsi, convention générateur, la puissance fournie par le dipôle à l'extérieur peut s'exprimer de la façon suivante : [ P _ text{ fournie } = U times I = left( E - R times I right) times I ] [ P _ text{ fournie } = E times I - R times I ^2 ] La puissance fournie par le dipôle actif correspond alors à la puissance fournie par un générateur idéal de tension, noté E, qui va donc délivrer un courant, noté I, dont une partie est dissipée par effet Joule, représenté par -RxI2 . Si on se concentre sur le cas des moteurs électriques, ExI est un terme représentant la puissance électromécanique que l'on note Pem.
La puissance au sein d'un régime alternatif
Le régime alternatif
Si la tension et le courant varient, on considère que la puissance instantanée consommée par un dipôle est représenté par le produit des valeurs instantanées du courant qui le traverse et de la tension à ses bornes. On obtient alors la formule suivante : [ p left(t right) = u left( t right) times i left( t right) ] Si on se considère en régime sinusoïdal, on peut exprimer la tension et l'intensité de la façon suivante : [\begin{cases} i left( t right) = i _ 0 times cos left( omega t right) = I \sqrt { 2 } times cos left( omega t right) u left( t right) = u _ 0 times cos left( omega t + phi right) = U \sqrt { 2 } times cos left( omega t + phi right) \end{cases} ] Avec :
- U et I sont les valeurs efficaces de la tension et du courant
- Et Φ est le déphasage de la tension par rapport au courant.
On obtient alors l'expression de la puissance suivante : [p left( t right) = Utimes I times cos left( phi right) + U times I times cos left( 2 times omega t + phi right) ] Il peut alors être intéressant de noter que le premier terme de la somme ci-dessus correspond à la puissance active alors que le second terme correspond à la puissance sinusoïdale de fréquence qui est double de celle du courant et de la tension. La position moyenne de cette puissance sinusoïdale est d'ailleurs égale à la puissance active. De plus, la valeur de cos(Φ) correspond quant à lui au facteur de puissance en régime sinusoïdal. On appelle ainsi puissance fluctuante une puissance sinusoïdale de fréquence double de celle du courant et de la tension. Cette puissance n'a, pour les convertisseurs électrothermique, aucun effet puisque l'inertie thermique du système permet de lisser et ce de façon totale les variations de puissance. Cependant, cela n'est pas vrai pour les conversion électromécanique puisque la machine électrique, qu'elle soit moteur ou génératrice, tourne avec une vitesse presque constante grâce à son inertie. De ce fait, à chaque instant elle consomme ou fournir, modulo des pertes, une puissance mécanique identique. Ainsi, la puissance fluctuante est responsable d'oscillations de couples qui sont, pour la majeure partie, absorbée par l'élasticité de l'arbre de transmission. C'est pour cela que, pour une machine de forte puissance, ces oscillations sont à éviter puisqu'elles risque de provoquer la destruction de cette machine. Ceci étant la raison par laquelle les alternateurs de centrales électrique ou encore les très gros moteurs se doivent d'être polyphasés. Dans les fait, ils sont généralement triphasés.
Le travail électrique

Un dipôle parcouru par un courant d'intensité I échange de l'énergie avec le reste du circuit. Le mode de transfert est le travail des forces électriques.
Pendant la durée t, les forces électriques s'exerçant sur les charges qui traversent un dipôle AB, parcouru par un courant d'intensité I circulant de A vers B effectuent le travail : [ W _ { AB } = U _ { AB } times I times t ]
De par la définition de la puissance , il est possible de savoir que la puissance des forces électriques correspond à : [ P _ { AB } = U _ { AB } times I ]
Ainsi, on sait que :
- Si la puissance est positive, alors le dipôle AB a reçu cette puissance.
- Si la puissance est négative, alors le dipôle AB a cédé cette puissance.
Avec :
- La tension U qui s'exprime en volt (V) ;
- L'intensité I qui s'exprime en ampère (A) ;
- Le temps t qui s'exprime en seconde (s) ;
- Le travail W qui s'exprime en joule (J) ;
- Et la puissance P qui s'exprime en watt (W).
On sait que, lorsqu'un dipôle est traversé par un courant, il y a transfert d'énergie entre le dipôle et le milieu ambiant.
De ce fait, lorsque le circuit est traversé par un courant d'intensité I, alors peu importe le dipôle présent au sein de ce circuit, celui-ci va s'échauffer. On appelle cela l'effet Joule. De ce fait, le dipôle qui sera ainsi échauffé va céder de l'énergie par chaleur au milieu ambiant.
On sait également que lorsqu'il le dipôle est traversé par un courant, alors celui-ci est capable d'effectuer un travail (on le considère alors comme un moteur électrique). Il cède alors de l'énergie au milieu ambiant par travail.
Par la même façon, lorsque le dipôle est traversé par un courant, alors celui-ci est capable d'émettre de la lumière (on le considère alors comme lampe électrique). Il cède alors de l'énergie au milieu ambiant.
La loi d'ohm s'écrit, pour un courant traversant le conducteur ohmique de A vers B : [ U _ { AB } = R times I ] où R est la résistance du conducteur ohmique.
Tandis que la loi de Joule s'exprime ainsi : [ P _ { AB } = R times I ^ 2 ]
Cette puissance est toujours positive. Un conducteur ohmique reçoit de l'énergie du reste du circuit. Le dipôle s'échauffe. Puis sa température reste constante : à chaque instant, l'énergie reçue du reste du circuit par travail des forces électriques est cédée au milieu ambiant par chaleur. La puissance [ P _ { AB } = R times I ^ 2 ] correspond à l'effet Joule.
Exercice : la force de l'outil éolien

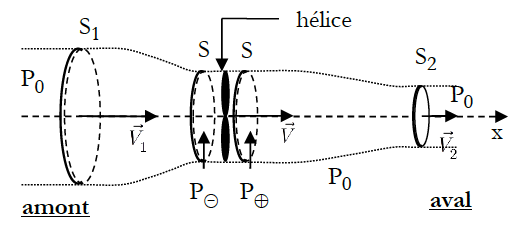
- Déterminer p- - p+ en fonction de μ, V1 et V2 .
- Établir par deux bilans de quantité de mouvement sur des systèmes bien choisis deux expressions de la force exercée par le fluide sur l'hélice : Fh.
- En déduire que V=(V1+V2)/2.
- Déterminer la puissance Ph recue par l'hélice et montrer que Ph= Fh.V
- On pose V=λV1. On définit le rendement r de l'éolienne comme le rapport de la puissance qu’elle reçoit avec la puissance que recevrait l’aire S, sous forme cinétique, en l’absence de l’hélice.
- Montrer que r=4λ2(1-λ) et déterminer sa valeur maximale, λ variant de 0 à 1.
Résumer avec l'IA :























Si vous désirez une aide personnalisée, contactez dès maintenant l’un de nos professeurs !