A partir de l'equation normale on retrouve la formule des MCO: On sait que la matrice X (les variables explicatives) et les résidus (epsilon) sont orthogonaux donc (c'est l'equation normale)
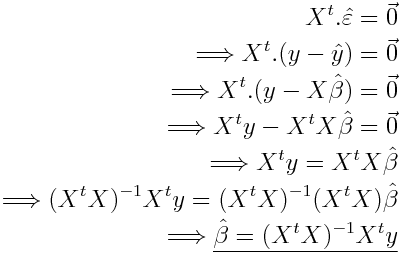
Avec la formule suivant on retrouve la matrice P et on en déduit qu'elle est idempotente:
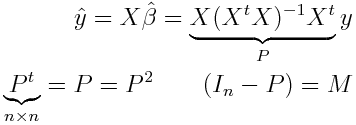
On sait aussi que le rang de P est le même que celui de X et donc on a:
rang P= k ; rang M = rang I - rang P= n-k
Avec ces formules on remarque que les résidus sont égaux à la matrice M.y
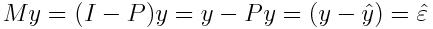
Calculons la distance entre le vecteur y c'est à dire les variables à expliquer et sa valeur moyenne ( y barre):
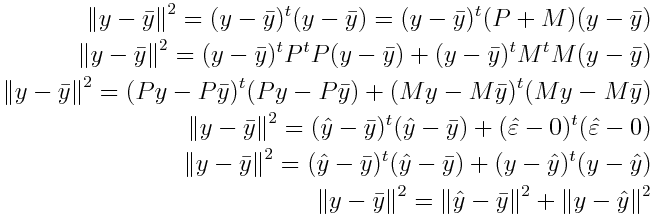
Or cette écart quand on la divise par le nombre de variables explicatives est la variance. On a donc:
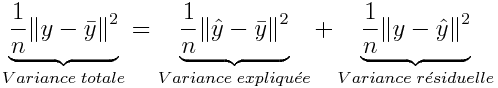
Avec cela on calcule le coefficient de détérmination: la variance expliquée divisée par la variance totale. C'est le pourcentage de variance que notre modèle exiplique par rapport au modèle véritable ( le PGD vrai):
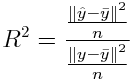
Résumer avec l'IA :










Si vous désirez une aide personnalisée, contactez dès maintenant l’un de nos professeurs !