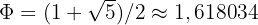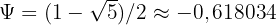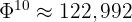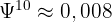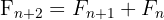
avec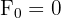 
, 
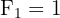, et pour tout 
, 
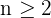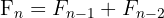
0, 1, 1, 2, 3, 5, 8, 13… Cette suite de nombres cache l'une des formules mathématiques les plus fascinantes et utiles de l'histoire : la suite de Fibonacci !
La suite de Fibonacci fonctionne selon un principe élémentaire : chaque nombre est la somme des deux précédents, en partant de 0 et 1. Introduite en Europe au XIIIe siècle par le mathématicien italien Leonardo Fibonacci dans son Liber Abaci (1202), cette suite a révolutionné notre compréhension des mathématiques.
Huit siècles plus tard, elle continue d'émerveiller : des spirales de tournesols aux algorithmes informatiques, des proportions du Parthénon aux compositions de Debussy, elle révèle une harmonie universelle entre nombres et réalité.
Dans cet article, nous vous présentons :
- L'histoire de la suite de Fibonacci (où il est question de lapins !)
- Le fonctionnement de la suite pour savoir comment calculer les premiers termes (et les suivants)
- Ainsi que quelques propriétés de la suite de Fibonacci (dont le lien avec le fameux nombre d'or).
Les origines historiques et mathématiques de la suite de Fibonacci
Découverte au XIIIe siècle, la suite de Fibonacci s'est progressivement imposée comme l'un des objets mathématiques les plus étudiés et les plus riches en applications.
Dans cette partie, nous revenons sur le rôle de Leonardo Fibonacci dans la démocratisation de l'utilisation des chiffres indo-arabes, sur le livre fondateur Liber Abaci et sur le célèbre problème des lapins.
Leonardo Fibonacci, le marchand révolutionnaire (des mathématiques)
Leonardo Fibonacci, de son vrai nom Leonardo Pisano (ce qui signifie "Léonard de Pise"), naît vers 1170 dans la République maritime de Pise1.
C'est dans un contexte cosmopolite, au carrefour des civilisations européenne, arabe et byzantine, que le jeune Leonardo reçoit une éducation exceptionnelle pour son époque. Son père l'emmène dans ses voyages commerciaux à travers le bassin méditerranéen : Égypte, Syrie, Grèce, Sicile et Provence.
Au contact des savants arabes et des marchands orientaux, Fibonacci découvre un système de numération révolutionnaire : les chiffres indo-arabes (0, 1, 2, 3, 4, 5, 6, 7, 8, 9) et le concept du zéro, qui facilitent considérablement les calculs par rapport aux chiffres romains (I, V, X, L, C, D, M) encore utilisés en Europe.
Le Liber Abaci : le livre qui a bouleversé l'Europe
De retour à Pise vers 1200, Fibonacci rédige en 1202 son œuvre majeure : le Liber Abaci (littéralement "Le Livre du calcul" ou "Le Livre de l'abaque"). Contrairement à ce que suggère son titre, cet ouvrage ne traite pas de l'abaque (boulier), mais bien du calcul avec les nouveaux chiffres indo-arabes.
Le Liber Abaci est une véritable encyclopédie commerciale et mathématique qui présente :
- Le système de numération décimale et positionnel
- Les quatre opérations arithmétiques de base
- Le calcul des fractions
- Les conversions de monnaies et de mesures
- Des problèmes de partage et de proportions
- Des applications commerciales (calcul d'intérêts, règles d'alliage, etc.)
L'influence arabe et indienne est manifeste : Fibonacci cite explicitement les mathématiciens arabes et reconnaît que leur système est la méthode des Indiens.
Les chiffres que nous utilisons aujourd'hui ont été inventés en Inde vers le Ve siècle, perfectionnés par les mathématiciens persans et arabes (notamment Al-Khwarizmi au IXe siècle).
Le passage des chiffres romains aux indo-arabes ne s'est évidemment pas fait du jour au lendemain. Il a fallu près de trois siècles pour que le nouveau système s'impose dans les universités, les commerces et les administrations européennes.
Mais l'efficacité du système décimal était telle que son adoption était inéluctable : là où il fallait des lignes de calcul avec les chiffres romains, quelques opérations suffisaient désormais.
Le célèbre problème des lapins
C'est au chapitre 12 du Liber Abaci2, dans une section consacrée aux problèmes récréatifs, que Fibonacci introduit le problème qui va immortaliser son nom.
Combien de couples de lapins obtiendra-t-on en un an si, commençant avec un seul couple, chaque couple engendre tous les mois un nouveau couple, lequel devient productif au bout d'un mois ?
Leonardo Fibonacci
Mois 1
1 couple
Vous commencez avec 1 couple de lapins nouveau-nés (appelons-les couple A). Ce couple est encore immature et ne peut pas se reproduire.
Mois 2
1 couple (le couple A)
Le couple A a grandi, mais il vient tout juste d'atteindre la maturité. Il va pouvoir se reproduire le mois suivant.
Mois 3
2 couples (A adulte, B immature)
Le couple A donne naissance à un nouveau couple (couple B). Le couple B est nouveau-né, donc immature.
Mois 4
3 couples (A adulte, B mature, C immature)
Le couple A donne naissance à un nouveau couple (couple C). Le couple B atteint la maturité mais ne se reproduit pas encore.
Mois 5
5 couples (A et B adultes, C mature, D et E immatures)
Le couple A donne naissance au couple D. Le couple B, désormais mature, donne naissance au couple E. Le couple C atteint la maturité.
Mois 6
8 couples (A, B et C adultes, D et E matures, F, G et H immatures)
Les couples A, B et C se reproduisent (3 nouveaux couples). Les couples D et E atteignent la maturité.
Le schéma se poursuit ainsi, et voici la progression complète sur 12 mois :
| Mois | Couple adulte (en âge de se reproduire) | Couple mature (pas encore l'âge de se reproduire) | Couple immature (nouveau-né) | Total |
|---|---|---|---|---|
| 1 | 0 | 0 | 1 | 1 |
| 2 | 0 | 1 | 0 | 1 |
| 3 | 1 | 0 | 1 | 2 |
| 4 | 1 | 1 | 1 | 3 |
| 5 | 2 | 1 | 2 | 5 |
| 6 | 3 | 2 | 3 | 8 |
| 7 | 5 | 3 | 5 | 13 |
| 8 | 8 | 5 | 8 | 21 |
| 9 | 13 | 8 | 13 | 34 |
| 10 | 21 | 13 | 21 | 55 |
| 11 | 34 | 21 | 34 | 89 |
| 12 | 55 | 34 | 44 | 144 |
Chaque mois, le nombre total de couples est égal à la somme du mois précédent (tous les couples survivent) et du mois d'avant-avant (ce sont les couples qui étaient déjà adultes à ce moment-là et qui donnent naissance).
Couples(mois n) = Couples(mois n-1) + Couples(mois n-2)
C'est exactement la définition de la suite de Fibonacci ! Même si le modèle biologique est évidemment irréaliste (pas de mortalité, reproduction régulière comme une horloge, cycle de maturation fixe), il illustre parfaitement le principe de récurrence au cœur de cette suite.
Fibonacci lui-même n'a jamais appelé cette suite par son nom. Ce n'est qu'au XIXe siècle que le mathématicien français Édouard Lucas (1842-1891) a baptisé cette séquence "suite de Fibonacci" en hommage à son découvreur. Fibonacci est également connu pour d'autres contributions : la barre de fraction (pour écrire les fractions), des travaux sur les nombres premiers, et une approximation du nombre π.
Savez-vous que le nombre d'or est aussi lié à la spiritualité ?
Comment fonctionne la suite de Fibonacci ?
Intéressons-nous de plus près au fonctionnement de la suite de Fibonacci.
La relation de récurrence au cœur du système
La beauté de la suite de Fibonacci réside dans sa simplicité déconcertante. Voici sa définition formelle :
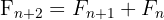avec ,
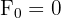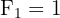
Pour obtenir un terme de la suite, il suffit d'additionner les deux termes qui le précèdent. C'est ce qu'on appelle une relation de récurrence d'ordre 2 (car elle fait intervenir les deux termes précédents).
Cette définition récursive est fondamentale en mathématiques et en informatique : elle permet de décrire une infinité de valeurs avec seulement deux informations initiales et une règle simple.
Le calcul des premiers termes de la suite de Fibonacci pas à pas
Mettons en pratique cette règle pour construire les premiers termes de la suite3 :
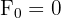(par définition) 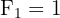(par définition)
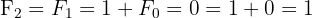(on additionne les deux termes précédents).
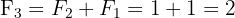(chaque nouveau terme utilise les deux précédents)
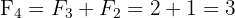
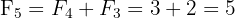
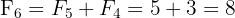
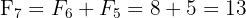
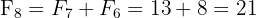
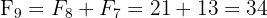
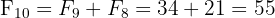
En étudiant ce tableau, deux propriétés remarquables émergent :
- La suite augmente très rapidement. Entre
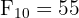et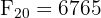 
, le terme a été multiplié par plus de 120 ! - On observe la parité (pair/impair) des termes : impair (1), impair (1), pair (2), impair (3), impair (5), pair (8), impair (13), impair (21), pair (34)... Le motif se répète : impair, impair, pair, impair, impair, pair... avec un cycle de période 3.
La formule de Binet : calculer directement n'importe quel terme
Le calcul itératif (additionner les termes un par un comme on vient de le faire) est simple mais fastidieux pour les grands rangs. Imaginez calculer F₁₀₀ à la main : il faudrait faire 99 additions successives !
Heureusement, la formule de Binet4 permet de calculer directement n'importe quel terme de Fibonacci sans passer par tous les précédents :
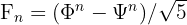
où :
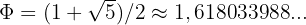(le nombre d'or)
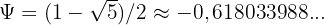(le "conjugué" du nombre d'or)
Calculons F₁₀ avec la formule de Binet :
Étape 1 : Calculer φ et ψ
Étape 2 : Calculer φ¹⁰ et ψ¹⁰
Étape 3 : Appliquer la formule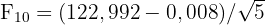 
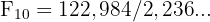
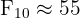
Le résultat est bien F₁₀ = 55, comme nous l'avions calculé manuellement !
Les propriétés de la suite Fibonacci
Au-delà de sa définition simple, la suite de Fibonacci recèle des propriétés mathématiques extraordinaires. Deux aspects retiennent particulièrement l'attention : leur convergence mystérieuse vers le nombre d'or et leurs propriétés arithmétiques surprenantes.
Le lien avec le nombre d'or
Calculons les rapports entre termes consécutifs de la suite :
- F₂/F₁ = 1/1 = 1
- F₃/F₂ = 2/1 = 2
- F₄/F₃ = 3/2 = 1,5
- F₅/F₄ = 5/3 ≈ 1,667
- F₆/F₅ = 8/5 = 1,6
- F₁₀/F₉ = 55/34 ≈ 1,617647
- F₂₀/F₁₉ = 6765/4181 ≈ 1,618034
- F₅₀/F₄₉ ≈ 1,618033988749...
Ce rapport converge vers une valeur précise appelée nombre d'or (φ, prononcé "phi")
Mathématiquement, on note :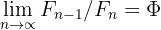 
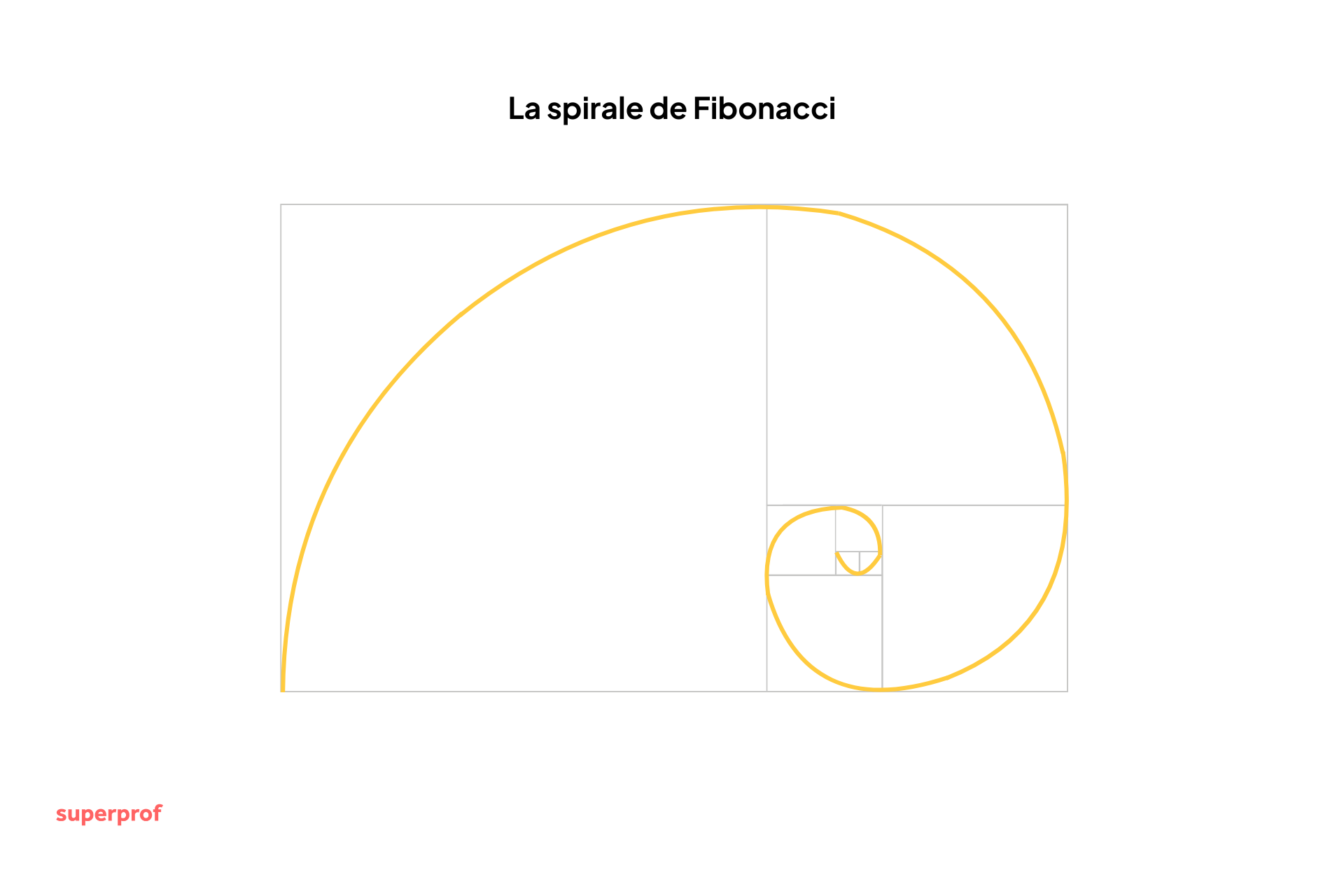
Le nombre d'or possède une propriété géométrique remarquable : un rectangle dont les côtés sont dans le rapport φ (le "rectangle d'or") peut être décomposé en un carré et un rectangle plus petit... également d'or ! En répétant cette opération et en traçant des arcs de cercle dans chaque carré, on obtient la célèbre spirale de Fibonacci, qu'on retrouve dans les coquillages nautiles, les galaxies spirales et les compositions artistiques.
Les propriétés mathématiques avancées
La suite de Fibonacci possède des propriétés de divisibilité étonnantes :
- Règle de divisibilité : Si n divise m, alors Fₙ divise Fₘ. Par exemple, F₃ = 2 divise F₆ = 8, F₉ = 34, F₁₂ = 144...
- Parité cyclique : La suite suit un motif impair-impair-pair qui se répète tous les 3 termes
- PGCD remarquable : PGCD(Fₙ, Fₘ) = F_PGCD(n,m)
En mathématiques avancées, les nombres de Fibonacci apparaissent dans des contextes surprenants :
- Dénombrement : Fₙ compte le nombre de façons de paver un rectangle 1×(n-1) avec des dominos 1×1 et 1×2
- Théorie des graphes : Fₙ représente le nombre de sous-ensembles indépendants dans un graphe en chemin de longueur n
- Suites modulo : La suite de Fibonacci modulo m (appelée suite de Pisano) est toujours périodique, avec des périodes fascinantes
Ces propriétés font de la suite de Fibonacci un objet mathématique fondamental qui continue d'alimenter la recherche contemporaine.
La suite de Fibonacci est partout autour de nous et dans différentes disciplines :
🧮 En mathématiques et en informatique : dans les algorithmes récursifs, les structures de données...
🌸 Dans la nature : structure d'un tournesol, pommes de pin, galaxies, coquillages...
🖼 En art : dans le design et les proportions de certains tableaux (comme la Joconde)
🏛 En architecture : notamment chez Le Corbusier mais aussi le Parthénon
🎶 En musique : chez Debussy notamment
Mais aussi dans le code génétique, dans certains jeux (comme au casino) ou encore sur les marchés financiers.
Avez-vous déjà repéré la suite de Fibonacci autour de vous ?
De l'énigme médiévale des lapins de Fibonacci aux algorithmes qui régissent nos smartphones, cette suite millénaire n'a cessé de tisser des liens entre mathématiques et réalité (présence du nombre d'or dans de nombreux domaines comme l'art).
Mais Fibonacci n'est qu'une porte d'entrée vers un univers mathématique encore plus vaste : suites récurrentes, programmation dynamique, théorie des nombres... Chaque niveau de compréhension révèle de nouvelles profondeurs.
Définition : Chaque terme = somme des deux précédents (0, 1, 1, 2, 3, 5, 8, 13...)
Formule récursive : F(n) = F(n-1) + F(n-2), avec F(0)=0 et F(1)=1
Nombre d'or φ : Limite du rapport F(n+1)/F(n) ≈ 1,618...
Formule de Binet : Calcul direct sans récursion : F(n) = [φⁿ - (-φ)⁻ⁿ] / √5
Sources
- Devlin, Keith. The Man of Numbers: Fibonacci's Arithmetic Revolution. Walker & Company, 2011. Disponible à https://archive.org/details/B-001-001-284 Consulté le 19 novembre 2025
- Fibonacci, Leonardo. Liber Abaci [1202]. Translated by Laurence E. Sigler, Springer, 2002. Disponible à https://www.mifami.org/eLibrary/Fibonacci-LiberAbaci-QuadClass-2pp.pdf Consulté le 19 novembre 2025
- Koshy, Thomas. Fibonacci and Lucas Numbers with Applications. Vol. 1, John Wiley & Sons, 2001. Disponible à https://onlinelibrary.wiley.com/doi/book/10.1002/9781118033067 Consulté le 19 novembre 2025
- Delahaye, Jean-Paul. "La suite de Fibonacci et ses suites." Pour la Science, 26 juillet 2017. Disponible à https://www.pourlascience.fr/sd/logique/la-suite-de-fibonacci-et-ses-suites-9757.php Consulté le 19 novembre 2025
Vous avez aimé cet article ? Notez-le !
Loading...
