Depuis l'Antiquité, le nombre d'or fascine par sa présence dans les structures naturelles.
Des spirales des coquillages aux pétales de fleurs, en passant par certaines proportions animales, ce rapport mathématique semble tisser un lien mystérieux entre géométrie et biologie.
Mais cette omniprésence est-elle réelle ou relève-t-elle d'une projection humaine ?
Entre tournesols mathématiquement organisés, mythes tenaces sur les coquilles de nautile et proportions corporelles fantasmées, explorons ce que la science confirme (ou réfute) sur le nombre d'or dans la nature.
Qu'est-ce que le nombre d'or dans la nature ?
Le nombre d'or (φ, phi) est défini mathématiquement comme :
φ = (1 + √5) / 2 ≈ 1,618
Ce nombre irrationnel possède une propriété unique : φ² = φ + 1. Cette relation crée une harmonie proportionnelle auto-similaire visible dans les rectangles d'or et les spirales logarithmiques.
Le nombre d'or entretient un lien étroit avec la suite de Fibonacci (0, 1, 1, 2, 3, 5, 8, 13, 21, 34...), où chaque nombre est la somme des deux précédents. Plus on avance dans cette suite, plus le rapport entre deux nombres consécutifs (21/13, 34/21...) se rapproche de φ.
Parce qu'elle apparaît spontanément dans des processus de croissance optimisée : disposition de feuilles maximisant la captation de lumière, spirales minimisant l'espace perdu... La nature ne "calcule" pas φ, mais l'évolution a sélectionné des configurations qui, par hasard mathématique, s'en approchent.
Où se trouve le nombre d'or dans la nature ?
Le nombre d'or chez les plantes
La phyllotaxie (du grec phyllon, feuille, et taxis, arrangement) désigne la disposition géométrique des feuilles, graines ou pétales sur une tige. C'est ici que le nombre d'or trouve ses manifestations les plus spectaculaires et scientifiquement validées.
Le tournesol : une perfection mathématique
Quand on observe attentivement le cœur d'un tournesol mature, on distingue deux familles de spirales qui s'entrecroisent :
spirales
spirales
Ces nombres appartiennent à la suite de Fibonacci ! Leur rapport (89/55 ≈ 1,618) approche φ avec une précision remarquable.
En 1979, le biologiste Helmut Vogel a démontré mathématiquement que cette disposition permet de maximiser le nombre de graines dans un espace circulaire limité1. Le modèle repose sur un angle de divergence entre graines successives de 137,5° (appelé "angle d'or"), directement lié à φ par la formule :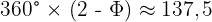 
. Cette configuration évite les alignements radiaux qui créeraient des zones vides.
Les pommes de pin et le chou romanesco
Quand on compte les spirales formées par les écailles d'une pomme de pin, on trouve généralement d'autres nombres de Fibonacci :
spirales.
spirales.
Parfois, selon l'espèce, vous observerez les paires 5/8 ou 13/21. Faites le test : prenez une pomme de pin et regardez-la d'en haut (le haut étant l'endroit où les écailles sont le plus fermées). Vous verrez des écailles (les petites protubérances ligneuses) disposées en lignes courbes qui semblent tourner autour de l'axe central.
Mais il y a bien deux familles de spirales qui s'entrecroisent. Comptez le nombre de spirales qui tournent dans un sens et comptez ensuite le nombre de spirales qui tournent dans l'autre sens.
Le chou romanesco offre un spectacle : chaque bourgeon forme une spirale logarithmique composée elle-même de spirales plus petites. On compte typiquement 5 spirales dans un sens, 8 dans l'autre au premier niveau, puis 8 et 13 au niveau suivant.
Cette structure fractale découle du même principe d'auto-organisation que le tournesol. Des simulations de Douady et Couder (1996) ont reproduit ces motifs en modélisant simplement la répulsion physique entre bourgeons émergents et l'angle d'or2.
Parce que 137,5° est un nombre irrationnel : les feuilles ne s'alignent jamais verticalement, garantissant une répartition équitable de lumière et de pluie. C'est un mécanisme d'optimisation évolutive3.
Le nombre d'or chez les animaux
Si la présence de φ chez les plantes repose sur des bases scientifiques solides, le monde animal présente un tableau bien plus nuancé, où mythes et réalités s'entremêlent.
L'étoile de mer commune présente une symétrie pentaradiale : cinq bras disposés régulièrement autour d'un centre. Cette géométrie n'est pas anodine : dans tout pentagone régulier, le rapport entre la longueur de la diagonale et celle du côté égale exactement φ.
Mathématiquement, cela découle de l'équation :
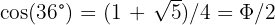
Le pentagone "contient" intrinsèquement le nombre d'or. Cette symétrie n'est pas une "recherche de beauté", mais une contrainte embryologique ancestrale chez les échinodermes, héritée de leurs ancêtres du Cambrien (il y a 540 millions d'années)4.
Les coquilles d'escargot et les ammonites par exemple présentent des spirales logarithmiques avec des ratios variables selon l'espèce et le nombre d'or n'est qu'une possibilité parmi d'autres5. Pour les plumes de paon, aucune étude scientifique ne valide un lien entre les motifs du paon et le nombre d'or ou Fibonacci6.
La fascination du nombre d'or se retrouve aussi en architecture.
Le nombre d'or, beauté naturelle ou projection humaine ?
Même si le nombre d'or est présent naturellement dans la nature, on peut se demander pourquoi on le perçoit comme beau et harmonieux et s'il a une vraie fonction.
Pourquoi associe-t-on le nombre d'or à la beauté ?
Depuis la Renaissance, artistes et architectes ont cherché à codifier l'harmonie par des proportions mathématiques. Le nombre d'or, surnommé "divine proportion" par Luca Pacioli (1509), semblait incarner cette quête.
Des études psychologiques ont testé si les humains préfèrent spontanément les rectangles d'or. Une méta-analyse de McManus et al. (2010)7 montre que les préférences varient énormément d'un individu à l'autre, et qu'aucun ratio (y compris le nombre d'or) ne se détache comme "universellement préféré".
Quand on "cherche" φ dans la nature ou l'art, on finit toujours par le trouver. C'est le paradoxe de la rétrospection : sur un objet complexe, on peut tracer des dizaines de rapports. Si l'un approche 1,6, on crie au nombre d'or en ignorant les 50 autres qui ne correspondent pas.
Les théories biologiques : quand le nombre d'or est vraiment utile
Contrairement aux mythes esthétiques, certaines manifestations naturelles de φ répondent à des pressions évolutives documentées.
C'est le cas pour l'optimisation de l'espace chez les plantes.
L'angle d'or (137,5°) ne peut être approximé par une fraction simple. Si les feuilles étaient espacées de 120° (1/3 de tour), elles s'aligneraient en 3 colonnes verticales, créant des zones d'ombre. Mais 137,5° étant irrationnel, les feuilles ne s'alignent jamais, garantissant une répartition optimale de lumière3.
Le nombre d'or dans la nature : réalité ou mythe ?
Au final, il est légitime de se demander si la présence du nombre d'or dans la nature est bien réelle ou si elle est mystifiée.
Le cas d'exagérations célèbres
Le nautile est probablement l'exemple le plus cité... et le plus erroné concernant le nombre d'or !
En s'appuyant sur la réalité scientifique, il n'en est rien. En 1988, Christopher Bartlett a mesuré précisément les spirales de nautiles8. La coquille suit bien une spirale logarithmique, mais avec un facteur de croissance ≈ 1,33 par quart de tour, et non 1,618.
Parce que toutes les spirales logarithmiques "se ressemblent visuellement" et que l'œil humain n'est pas assez précis pour distinguer un ratio de 1,33 d'un ratio de 1,618 sans mesure. Le nautile reste une merveille géométrique, mais pas un exemple de nombre d'or.
L'autre erreur la plus célèbre : les proportions du corps humain !
L'idée que le corps humain incarnerait des "proportions dorées" remonte à Vitruve et fut popularisée par Léonard de Vinci avec son Homme de Vitruve (1490).
En 1992, le mathématicien George Markowsky a mesuré ce ratio sur une douzaine de personnes9. Résultat : une moyenne d'environ 1,60, mais avec une large variation individuelle allant de 1,53 à 1,71. Ces données invalident l'idée d'une proportion φ universelle.
Le biologiste Mario Livio confirme dans The Golden Ratio (2002) : l'association φ/corps humain relève due la "pensée magique" et de la "rétrospection sélective"10. On choisit les mesures qui "fonctionnent" en ignorant les dizaines d'autres qui ne correspondent pas.
Ce que disent les études scientifiques
| Phénomène | Validation | Source |
|---|---|---|
| Phyllotaxie (tournesol, pomme de pin) | ✅ | Vogel (1979), Douady & Couder (1996) |
| Fractales végétales (romanesco) | ✅ | Douady & Couder (1996) |
| Pentagone régulier et étoiles de mer | ✅ | Géométrie classique + embryologie |
| Paon = spirales Fibonacci | ❌ | Aucune source scientifique |
| Nautile = spirale φ | ❌ | Ratio ≈ 1,33 (Bartlett 1988) |
| Corps humain = proportions φ | ❌ | Moyenne d'environ 1,60, (large variation individuelle) Markowsky (1992) |
Le nombre d'or existe réellement dans certains systèmes naturels, principalement végétaux, où il résulte de processus d'optimisation bien compris. Cependant, il n'est ni universel, ni magique : c'est un optimum parmi d'autres. Dans de nombreux cas célébrés (nautile, corps humain), sa "présence" relève de la projection humaine ou du mythe culturel.
✅ φ existe vraiment dans la phyllotaxie : tournesols, pommes de pin, choux romanesco présentent des spirales de Fibonacci (55/89, 8/13...) documentées scientifiquement.
✅ Le pentagone et l'étoile de mer : lien mathématique exact entre symétrie pentagonale et nombre d'or (diagonale/côté = φ).
❌ Le nautile n'est PAS une spirale d'or : son ratio de croissance (~1,33) diffère de φ. C'est le mythe le plus répandu.
❌ Le corps humain ne suit PAS des proportions φ universelles : les études anthropométriques montrent un ratio moyen de 1,60 avec forte variabilité individuelle.
⚠️ Beaucoup de "détections" de φ sont des projections a posteriori : biais de mesure, sélection des données, coïncidences amplifiées par répétition culturelle.
La nature utilise φ quand c'est optimal (phyllotaxie, fractales), mais pas comme "loi universelle". L'évolution favorise l'efficacité, pas la conformité mathématique !
Sources
- Vogel, Helmut. "A Better Way to Construct the Sunflower Head." Mathematical Biosciences, vol. 44, no. 3-4, 1979, pp. 179-189. Disponible à https://www.sciencedirect.com/science/article/abs/pii/0025556479900804 Consulté le 26 novembre 2025
- Douady, Stéphane, et Yves Couder. "Phyllotaxis as a Dynamical Self-Organizing Process." Journal of Theoretical Biology, vol. 178, no. 3, 1996, pp. 255-274. Disponible à https://comptes-rendus.academie-sciences.fr/mecanique/item/CRMECA_2020__348_6-7.pdf Consulté le 26 novembre 2025
- Jean, Roger V. Phyllotaxis: A Systemic Study in Plant Morphogenesis. Cambridge University Press, 1994. Disponible à https://archive.org/details/phyllotaxissyste0000jean/page/n5/mode/2up Consulté le 26 novembre 2025
- Hotchkiss, Frederick H. C. "A 'Rays-as-Appendages' Model for the Origin of Pentamerism in Echinoderms." Paleobiology, vol. 24, no. 2, 1998, pp. 200-214. Disponible à https://www.cambridge.org/core/journals/paleobiology/article/abs/raysasappendages-model-for-the-origin-of-pentamerism-in-echinoderms/D6BE57FA4F7EEACE5511B172C2B02827 Consulté le 25 novembre 2025
- Raup, David M. "Geometric Analysis of Shell Coiling: General Problems." Journal of Paleontology, vol. 40, no. 5, 1966, pp. 1178-1190. Disponible à https://www.jstor.org/stable/1301992 Consulté le 26 novembre 2025
- Prum, Richard O., et Rodolfo H. Torres. "Structural Colouration of Avian Skin: Convergent Evolution of Coherently Scattering Dermal Collagen Arrays." Journal of Experimental Biology, vol. 206, no. 14, 2003, pp. 2409-2429. Disponible à https://journals.biologists.com/jeb/article-abstract/206/14/2409/13691/Structural-colouration-of-avian-skin-convergent?redirectedFrom=fulltext Consulté le 26 novembre 2025
- McManus, I. C., et al. "Beyond the Golden Section and Normative Aesthetics: Why Do Individuals Differ So Much in Their Aesthetic Preferences for Rectangles?" Psychology of Aesthetics, Creativity, and the Arts, vol. 4, no. 2, 2010, pp. 113-126. Disponible à https://www.researchgate.net/publication/232577760_Beyond_the_Golden_Section_and_Normative_Aesthetics_Why_Do_Individuals_Differ_so_Much_in_Their_Aesthetic_Preferences_for_Rectangles Consulté le 25 novembre 2025
- Bartlett, Christopher. "The Nautilus Shell Spiral as a Golden Spiral." Fibonacci Quarterly, vol. 26, no. 4, 1988, pp. 388-389. Disponible à https://www.researchgate.net/publication/329606393_Nautilus_Spirals_and_the_Meta-Golden_Ratio_Chi Consulté le 25 novembre 2025
- Markowsky, George. "Misconceptions about the Golden Ratio." The College Mathematics Journal, vol. 23, no. 1, 1992, pp. 2-19. Disponible à https://www.researchgate.net/publication/322814290_Misconceptions_about_the_Golden_Ratio Consulté le 26 novembre 2025
- Livio, Mario. The Golden Ratio: The Story of Phi, the World's Most Astonishing Number. Broadway Books, 2002. Disponible à https://www.researchgate.net/publication/305268297_Mario_Livio-The_Golden_Ratio_The_Story_of_PHI_the_World's_Most_Astonishing_Number-Broadway_Books_2003 Consulté le 26 novembre 2025
Vous avez aimé cet article ? Notez-le !
Loading...
