Depuis l'Antiquité, architectes et bâtisseurs cherchent la formule de l'harmonie parfaite. Parmi les outils mathématiques utilisés, le nombre d'or occupe une place mythique.
et se retrouve un peu partout dans la nature.
Ce rapport, que l'on retrouve dans les pétales de tournesol fascine par son apparente universalité esthétique.
Mais au-delà du mythe, quelle est la réalité de son utilisation architecturale ?
Du Parthénon grec au Modulor de Le Corbusier, en passant par les créations contemporaines, explorons comment ce nombre influence (ou non) la conception des espaces qui nous entourent. Entre vérités historiques, légendes tenaces et applications modernes, nous dévoilons les secrets du nombre d'or en architecture.

Qu'est-ce que le nombre d'or en architecture ?
Le nombre d'or φ (phi) se définit mathématiquement comme la solution positive de l'équation x² = x + 1, soit :
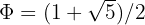
En architecture, ce rapport s'applique principalement au rectangle d'or : un rectangle dont le rapport longueur/largeur égale φ. Si on enlève un carré à ce rectangle, le rectangle restant conserve les mêmes proportions : une propriété unique qui crée une harmonie visuelle auto-similaire1.
Ce qui rend φ fascinant, c'est sa présence dans la nature notamment dans la disposition des feuilles sur une tige (phyllotaxie)2... Cela a conduit philosophes et architectes à y voir un "nombre divin", censé incarner la beauté universelle.
Si la nature "se sert" spontanément de ces proportions pour optimiser l'espace (captation de lumière, résistance structurelle...), les humains ont cherché à reproduire consciemment cette harmonie dans leurs constructions.
Mais cette intention était-elle toujours délibérée ? Là commence le débat...
Le nombre d'or dans l'histoire de l'architecture
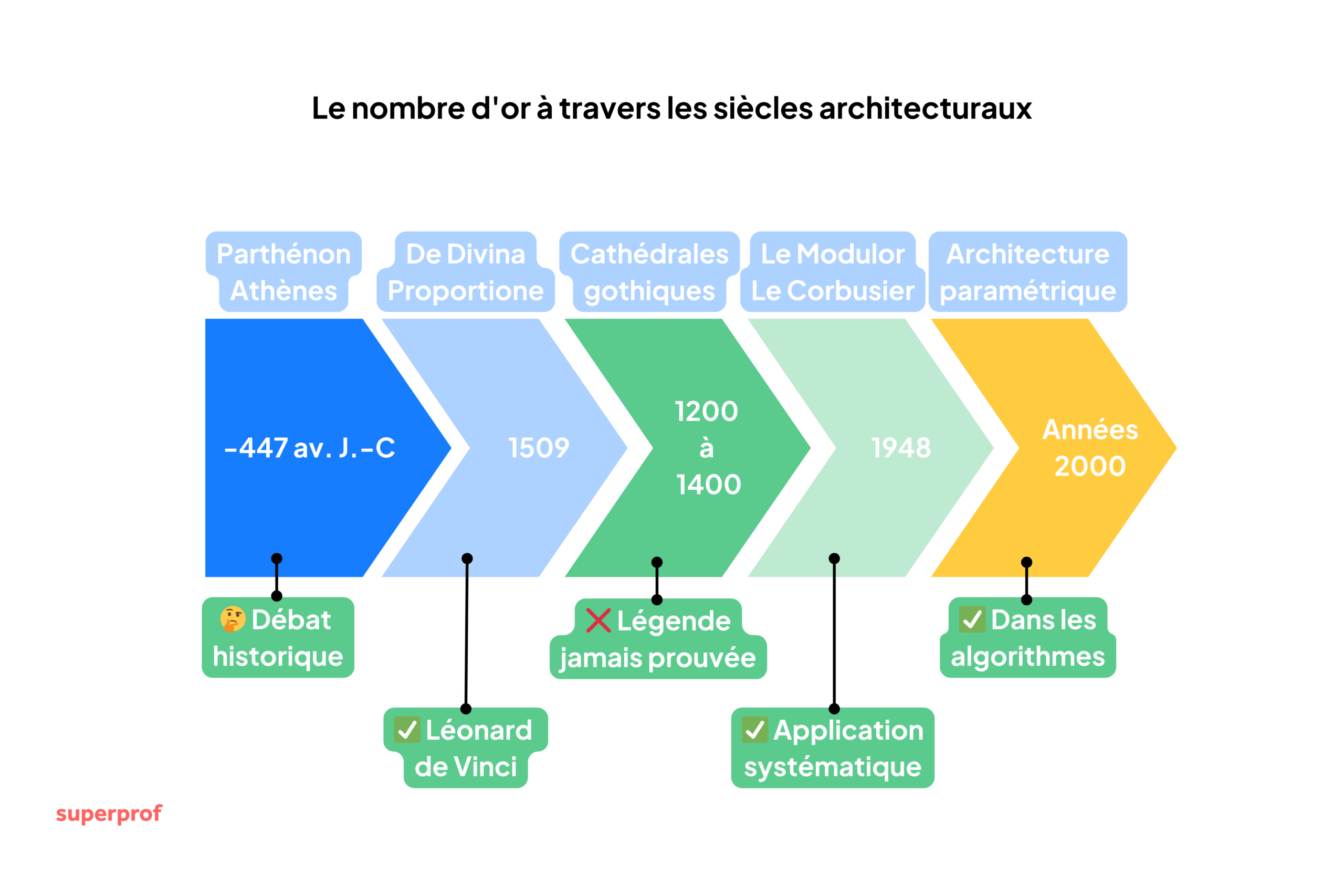
L'Antiquité : le mythe du Parthénon et des pyramides
Le Parthénon d'Athènes (447-432 av. J.-C.) est souvent cité comme exemple parfait du nombre d'or. En réalité, les historiens sont plutôt très divisés3 :
✅ Argument pour :
Le rapport hauteur/largeur de la façade approche 1,618.
❌ Argument contre :
Les Grecs utilisaient des fractions simples (3:2, 4:3) documentées dans les traités, pas φ qui nécessite √5
Encore plus contesté4 ! Roger Herz-Fischler a démontré que les proportions s'expliquent par des coudées égyptiennes (unité de mesure), pas par une intention mathématique sophistiquée. Le "mythe des pyramides d'or" date du XIXe siècle.
Le nombre d'or à la Renaissance : Pacioli et Léonard de Vinci
C'est véritablement à la Renaissance que φ entre dans la théorie architecturale.
En 1509, le moine mathématicien Luca Pacioli publie De Divina Proportione, illustré par Léonard de Vinci5. L'ouvrage codifie les proportions harmoniques, mais paradoxalement, De Vinci n'a jamais conçu de bâtiment utilisant systématiquement φ.

Beaucoup affirment que l'Homme de Vitruve "prouve" la présence du nombre d'or (φ ≈ 1,618) dans le corps humain. C'est majoritairement faux.
- De Vinci n'a jamais mentionné φ dans ses notes sur ce dessin
- Les proportions ne correspondent pas précisément à φ (par exemple, nombril/hauteur totale ≈ 0,618 est une approximation moderne forcée)
- Le cercle et le carré ne sont pas en rapport doré (le rapport côté carré/rayon cercle ≈ 1,414, soit √2, pas φ)
En revanche, on sait que De Vinci connaissait le nombre d'or (il a illustré De Divina Proportione de Pacioli en 1509, soit 19 ans après l'Homme de Vitruve). Certaines proportions s'approchent de φ (rapport main/avant-bras ≈ 1,6) mais c'est approximatif. Le dessin explore les rapports harmonieux (concept dont φ fait partie, mais n'est pas l'unique référence).
Selon l'analyse pixel par pixel de George Markowsky (mathématicien, université du Maine) et Mario Livio (astrophysicien) : aucune mesure ne donne exactement φ.
Quant aux cathédrales gothiques (Notre-Dame de Paris, Chartres...), aucun traité médiéval ne mentionne φ. Il s'agirait d'une légende urbaine (peut-être lié à la présence du nombre d'or dans la spiritualité). Les bâtisseurs utilisaient des techniques géométriques empiriques (triangulation, carrés tournés) sans référence explicite au nombre d'or6.
L'architecture moderne : Le Corbusier et le Modulor
Le véritable tournant arrive au XXe siècle avec Le Corbusier (1887-1965). En 1948, il développe le Modulor, système de proportions basé sur :
La taille humaine (1,83 m pour un homme le bras levé)
La suite de Fibonacci (qui converge vers φ)
Le nombre d'or comme générateur d'harmonie7
Voici deux applications concrètes :

L'Unité d'Habitation de Marseille (aussi appelée la Cité Radieuse), bâtie en 1952. Le Modulor a été utilisé pour les dimensions des appartements, des fenêtres et des balcons.
Architecte : Le Corbusier / Crédit photo : A.Savin
Le Couvent Sainte-Marie de La Tourette, construit entre 1953 et 1960. Les proportions des façades correspondent au Modulor.
Architecte : Le Corbusier / Crédit photo : Olivier Martin-Gambier, 2004

Le Modulor est un outil de mesure issu de la stature humaine et des mathématiques.
affirmait Le Corbusier (7)
Contrairement aux mythes antiques, ici l'usage de φ est documenté et intentionnel.

Comment le nombre d’or est-il utilisé aujourd’hui en architecture ?
Aujourd'hui, le nombre d'or se retrouve (ou non) dans l'architecture de certains bâtiments contemporains.
La conception de bâtiments contemporains à l'aide du nombre d'or
Aujourd'hui, le nombre d'or reste un outil parmi d'autres pour créer des proportions équilibrées. Il est couramment employé pour :
Les proportions de façades : rapport hauteur/largeur des bâtiments publics (musées, bibliothèques)
Les dimensions d'ouvertures : fenêtres, portes dont les proportions suivent φ
Les plans d'agencement : division d'espaces intérieurs selon le rectangle d'or
Car le cerveau humain perçoit les rapports proches de 1,6 comme "naturellement équilibrés" – ni trop carrés (1:1), ni trop étirés (3:1)8. Cette zone de confort visuel explique le succès persistant du nombre d'or (mais il n'est pas le seul).
Des exemples modernes analysés : attention aux idées reçues tenaces !
Le Siège de l'ONU est souvent cité comme exemple dans l'architecture avec le nombre d'or. Pourtant, il n'en est rien... Même si Le Corbusier a bien présenté un plan avec le Modulor, la version finale retenue (Harrison & Abramovitz) n'utilise PAS le nombre d'or. Le bâtiment suit des proportions fonctionnelles (étages de 3m, structure en béton...).
Contrairement à une idée répandue, Zaha Hadid n'a pas utilisé le nombre d'or comme principe directeur de sa conception architecturale. Elle s'appuyait sur des logiciels paramétriques, des algorithmes génératifs et sur la géométrie topologique.
Les limites et les controverses autour du nombre d'or en architecture
A trop chercher le nombre d'or, on le trouve ! C'est un biais qu'il est important de prendre en compte lorsqu'on analyse l'architecture : ne laissez pas de côté votre esprit critique et appuyez-vous sur des preuves formelles.
Le nombre d'or en architecture : mythe ou réalité ?
Il existe un problème méthodologique majeur : on retrouve φ... parce qu'on le cherche9.
Le mathématicien Mario Livio a démontré que :
- Les mesures du Parthénon varient selon les points de référence choisis
- On peut "trouver" φ dans n'importe quel bâtiment en sélectionnant les bonnes dimensions
- Aucun papyrus égyptien, aucun traité grec n'évoque explicitement φ en architecture3
Pour l'Antiquité et le Moyen Âge, l'utilisation de φ relève de la projection rétrospective. Seule l'architecture du XXe siècle (Le Corbusier notamment) l'a appliqué consciemment.
Les alternatives au nombre d'or et les approches contemporaines
Le nombre d'or n'est pas l'unique système proportionnel :
Le nombre plastique (ψ ≈ 1,3247)
Développé par l'architecte Dom Hans van der Laan, ce rapport offre des proportions plus "sobres" que φ10.
La règle des tiers
Plus connue en photographie, la règle des tiers consiste à diviser l'espace en 3×3 sections égales (rapport 1:2) pour créer un équilibre visuel efficace sans φ.
L'architecture algorithmique
Les logiciels modernes (Grasshopper, Rhino) permettent de générer des formes selon n'importe quel rapport mathématique. φ devient une option parmi des centaines de paramètres.11
Comment intégrer le nombre d'or dans un projet architectural ?
Aujourd'hui, il est facile d'intégrer le nombre dans un projet architectural.
Les outils et méthodes pratiques
Vous pouvez utiliser des logiciels CAO/DAO comme SketchUp et le plugin "Golden Ratio Calculator pour tracer des rectangles φ automatiquement. Rhino et Grasshopper permettent de créer des scripts paramétriques générant des spirales d'or pour des façades organiques. AutoCAD vous permet de créer des gabarits pré-configurés avec des grilles φ.

Vous pouvez aussi utiliser la méthode "à l'ancienne" pour tracer une spirale d'or à la main :
- Dessiner un carré
- Ajouter un rectangle dont la largeur est égale au côté du carré et la longueur est égale au côté × φ
- Répéter en créant un carré dans chaque nouveau rectangle
- Tracer des arcs de cercle dans chaque carré pour obtenir la spirale dorée.
Il existe aussi des applications mobiles comme "Phi Matrix" qui permet de superposer une grille φ sur des photos de bâtiments pour analyser leurs proportions.
Un cas pratique concret d'architecture avec le nombre d'or
Si vous voulez réaliser le plan d'une maison individuelle en utilisant environ le nombre d'or, voici quelques repères :
- Pour une pièce comme le salon : longueur = 6,48 m si largeur = 4 m (rapport 1,62)
- Pour vos fenêtres : hauteur 1,30 m pour largeur 0,80 m
Vous créez ainsi une sensation d'espace équilibré sans "effet couloir".
Attention : ce sont des dimensions inhabituelles en France. 6,48 m est une dimension très atypique (pas un multiple de 0,10 m ou 0,125 m comme dans les standards constructifs). Pour info, un salon standard français fait environ 20-30 m² donc 4×5 m ou 4×6 m.
Le nombre d'or a été utilisé en architecture principalement au XXe siècle :
❌ Antiquité/Moyen Âge : mythe largement infirmé (Parthénon, pyramides, cathédrales)
✅ XXe siècle : application documentée par Le Corbusier avec Le Modulor
🔄 Aujourd'hui : le nombre d'or est un outil parmi tant d'autres dans la conception
Sources
La plupart des sources académiques citées sont accessibles gratuitement via les bibliothèques universitaires françaises (Université Paris-Sorbonne, Lyon, Toulouse...) ou le portail Bibliothèque Nationale de France (https://www.bnf.fr).
- Livio, Mario. The Golden Ratio: The Story of Phi, the World's Most Astonishing Number. Broadway Books, 2002. Disponible à https://www.researchgate.net/publication/305268297_Mario_Livio-The_Golden_Ratio_The_Story_of_PHI_the_World's_Most_Astonishing_Number-Broadway_Books_2003 Consulté le 20 novembre 2025
- Dunlap, Richard A. The Golden Ratio and Fibonacci Numbers. World Scientific, 1997. Disponible à https://pdfcoffee.com/golden-ratio-and-fibonacci-numbers-pdf-free.html Consulté le 20 novembre 2025
- Markowsky, George. "Misconceptions about the Golden Ratio." The College Mathematics Journal, vol. 23, no. 1, 1992, pp. 2-19. Disponible à https://www.researchgate.net/publication/322814290_Misconceptions_about_the_Golden_Ratio Consulté le 20 novembre 2025
- Herz-Fischler, Roger. The Shape of the Great Pyramid. Wilfrid Laurier University Press, 2000. Disponible en version papier pour prêt à https://ccbmn.culture.gouv.fr/doc/SYRACUSE/784997/the-shape-of-the-great-pyramid-roger-herz-fischler Consulté le 25 novembre 2025
- Pacioli, Luca. De Divina Proportione. Venise, Paganini, 1509. (Réédition : Silvana Editoriale, 1982). Disponible à https://journals.openedition.org/sourcesarche/797 Consulté le 25 novembre 2025
- Bork, Robert. The Geometry of Creation: Architectural Drawing and the Dynamics of Gothic Design. Routledge, 2011. Extrait disponible à https://api.pageplace.de/preview/DT0400.9781351888981_A30906672/preview-9781351888981_A30906672.pdf Consulté le 25 novembre 2025
- Le Corbusier. Le Modulor: Essai sur une mesure harmonique à l'échelle humaine applicable universellement à l'architecture et à la mécanique. Éditions de l'Architecture d'Aujourd'hui, 1950. Disponible en version papier dans les bibliothèques universitaires
- McManus, I. C., et al. "Beyond the Golden Section and Normative Aesthetics: Why Do Individuals Differ So Much in Their Aesthetic Preferences for Rectangles?" Psychology of Aesthetics, Creativity, and the Arts, vol. 4, no. 2, 2010, pp. 113-126. Disponible à https://www.researchgate.net/publication/232577760_Beyond_the_Golden_Section_and_Normative_Aesthetics_Why_Do_Individuals_Differ_so_Much_in_Their_Aesthetic_Preferences_for_Rectangles Consulté le 25 novembre 2025
- Falbo, Clement. "The Golden Ratio—A Contrary Viewpoint." The College Mathematics Journal, vol. 36, no. 2, 2005, pp. 123-134. Disponible à https://www.researchgate.net/publication/247892441_The_Golden_Ratio-A_Contrary_Viewpoint Consulté le 25 novembre 2025
- Delahaye, Jean-Paul. "Le nombre plastique et ses cousins." Pour la Science, no. 428, juin 2013, pp. 78-83. Disponible en bibliothèque universitaire ou sur abonnement
- Migayrou, Frédéric (dir.). Architectures non standard. Éditions du Centre Pompidou, 2003. Disponible en version papier dans des bibliothèques françaises.
Résumer via IA :















