Chapitres
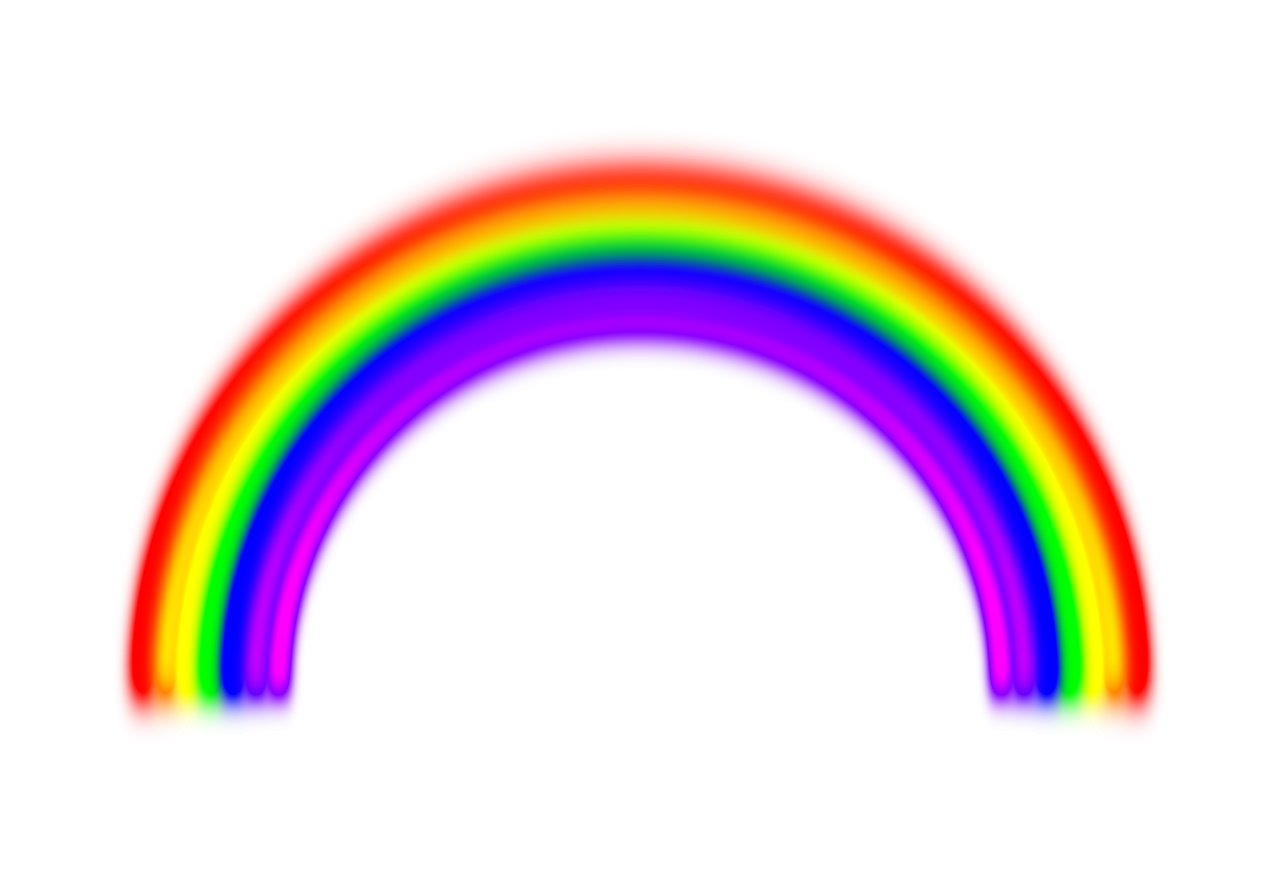
Un arc-en-ciel est un phénomène optique et météorologique qui rend visible le spectre continu de la lumière du ciel quand le soleil brille pendant la pluie. C'est un arc coloré avec le rouge à l'extérieur et le violet à l'intérieur.

La description physique de l'arc-en-ciel
On peut observer l'effet d'arc-en-ciel toutes les fois où il y a de l'eau en suspension dans l'air et qu'une source lumineuse (en général le Soleil) brille derrière l'observateur.
Les arcs-en-ciel les plus spectaculaires ont lieu lorsque la moitié du ciel opposée au Soleil est obscurcie par les nuages mais que l'observateur est à un endroit où le ciel est clair.
Un autre endroit commun où l'on peut voir cet effet est à proximité de chutes d'eau.
Sa position est toujours dans la direction opposée au soleil par rapport à l'observateur. Le centre de l'arc est toujours dans la direction de l'ombre de l'observateur ; l'arc lui-même apparaissant sous un angle approximatif de 40-42° au-dessus de cette
ligne soleil -observateur-centre de l'arc.
On peut aussi créer artificiellement cet effet un jour ensoleillé en se tournant dos au soleil puis dispersant des gouttelettes d'eau dans l'air devant soi (lors d'un arrosage par exemple) l'arc est alors d'autant plus visible que le fond est sombre.
Dans de rares cas, un arc-en-ciel peut être vu de nuit. Dans ce cas, c'est la Lune qui sert de source lumineuse. En pratique, la lumière de l'arc ainsi produit est faible et peut ne pas exciter suffisamment les cellules de la rétine responsables de la
perception de la couleur (les cônes). L'arc apparaît ainsi d'une lueur grisâtre sans couleur apparente. Les couleurs peuvent cependant apparaître sur une photo.
Le spectre de la lumière visible

Les couleurs de l'arc en ciel apparaissent dans un ordre bien précis. Voici un tableau qui les récapitule :
| Couleur | Rouge | Orange | Jaune | Vert | Bleu | Indigo | Violet |
|---|---|---|---|---|---|---|---|
| Longueur d'onde associée (en nm) | 650 | 590 | 570 | 510 | 475 | 445 | 400 |
Le spectre continu est un spectre lumineux composé de rayonnements électromagnétiques dont les longueurs d’onde varient de manière continue : cela implique qu’il ne s’achève pas de manière brutale à ses extrémités, mais qu’à ces dernières l’intensité des radiations décroit progressivement jusqu’à être nulle.
Cela suppose aussi que le spectre ne comporte pas de discontinuité et qu’il ne lui manque aucune longueur d’onde ou intervalle de longueur d’onde. Un spectre continu n’appartient pas forcément au domaine du visible, il peut appartenir à un autre intervalle de longueur d’onde comme ultraviolet ou infrarouge.
Les spectres continus sont des spectres d’origine thermique, cela signifie qu’ils sont obtenus à partir de sources (dans un état solide, liquide ou gazeux) portées à température suffisamment haute pour émettre de la lumière.
Une lumière à spectre continu est donc émise par tout corps incandescent, tel que du magma en fusion, des braises, le métal travaillé dans une forge ou le filament d’une lampe chauffé par effet Joule lors du passage du courant.
La lumière blanche est le seul spectre continu visible par l’homme. En effet, si la lumière a une couleur, le spectre n’est plus continu puisqu’il manque au moins une longueur d’onde.
Le soleil est effectivement une source chaude. En effet, la température à la surface du soleil est de plusieurs milliers de degrés, avoisinant les 6000 °C et la lumière qu’émet cette surface a bien un spectre continu.
Néanmoins, avant de nous parvenir, cette lumière doit traverser deux couches de gaz : tout d’abord celle qui entoure le soleil (la chromosphère), puis celle qui entoure la terre (l’atmosphère terrestre). Ces gaz absorbent certaines longueurs d’onde et font apparaître dans le spectre de la lumière solaire des raies noires : il ne s’agit plus d’un spectre continu, mais d’un spectre d’absorption.
Le spectre de la lumière du soleil est constitué de multiples raies noires, correspondant à l’absorption des éléments chimiques présents dans l’atmosphère terrestre et la chromosphère
Les discontinuités sombres qui y sont présentes sont également appelées les raies de Fraunhofer et correspondent chacune à l’interaction entre le rayonnement électromagnétique et un atome ou une molécule présents dans un état gazeux dans l’atmosphère terrestre.
Ces raies ont été étudiées par plusieurs scientifiques après leur découverte, ce qui a permit d’avoir les désignations précises pour toutes les longueurs d’onde absorbées.
Par exemple, les séries F, C, G’ et h correspondent aux différentes transitions électroniques dans l’atome d’hydrogène.
Remarque : si l’on décompose la lumière à l’aide d’un prisme ou d’un réseau, les raies d’absorption sont si fines qu’il n’est pas possible de les voir.
Dans le cas d’un spectre solaire et de l’absorption atmosphérique, on parle également des bandes d’absorption, représentant non pas une longueur d’onde (ou énergie de transition) unique mais une série de longueurs d’onde ou un intervalle continu couvrant une certaine plage spectrale selon le type de molécule participant au processus d’absorption.
Les bandes d’absorption existent car les molécules et les atomes ne peuvent absorber qu’une certaine quantité d’énergie. Une fois cette énergie absorbée, la molécule ou l’atome en question passe de son état initial à son état final. C’est cette transition entre les deux état qui crée la bande d’absorption au sein du spectre.
La formation de l'arc-en-ciel
L'arc-en-ciel est provoqué par la dispersion de la lumière du soleil par des gouttes de pluie approximativement sphériques.
La lumière est d'abord réfractée en pénétrant la surface de la goutte, subit ensuite une réflexion partielle à l'arrière de cette goutte et est réfractée à nouveau en sortant.
L'effet global est que la lumière entrante est réfléchie vers l'arrière sous un angle d'environ 40-42°, indépendamment de la taille de la goutte.
La valeur précise de l'angle de réflexion dépend de la longueur d'onde (la couleur) des composantes de la lumière.
La lumière bleue est réfractée à un plus grand angle que la lumière rouge, mais en raison de la réflexion totale, la lumière rouge apparaît plus haut dans le ciel et forme la couleur externe de l'arc-en-ciel.
Un arc-en-ciel n'a donc pas réellement d'existence physique mais est une illusion optique dont la position apparente dépend de la position de l'observateur. Toutes les gouttes de pluie réfractent et reflètent la lumière du soleil de la même manière, mais seulement la lumière d'une petite partie des gouttes de pluie atteint l’œil de l'observateur. C'est l'image formée par la lumière de ces gouttes de pluie que nous voyons sous forme d'arc-en-ciel.
D'un avion on peut voir le cercle entier de l'arc-en-ciel avec l'ombre de l'avion (donnant la direction opposée au Soleil) en son centre.

Les phénomènes physiques au sein de l'arc en ciel
Lors de la formation d'un arc en ciel, plusieurs phénomènes physiques apparaissent. C'est le cas notamment du phénomène de réfraction.
Lorsque la lumière provient à notre œil, celle-ci passe du milieu extérieur à notre œil et est donc déviée de sa trajectoire initiale.
Un phénomène de réfraction a donc lieu. On note l'indice de réfraction n. Celui-ci mesure la capacité d'un milieu à ralentir la vitesse de la lumière. Voici son expression :
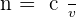
Avec :
- c la célérité de la lumière dans le vide : 299 792 458 m / s ;
- v vitesse de la lumière dans le milieu pris en considération.
La Loi de Snell-Descartes
Rappels
Le rayon lumineux est dit incident avant d'avoir rencontré la surface réfractante (appelée dioptre), il est dit réfracté après avoir rencontré cette dernière.
Le point de rencontre du rayon incident et du dioptre est appelé point d'incidence.
Le plan contenant le rayon incident et la normale au dioptre, au point d'incidence est dit plan d'incidence.
L'angle orienté i1 pris entre la normale au point d'incidence et le rayon incident est dit angle d'incidence.
L'angle orienté i2 pris entre la normale au point d'incidence et le rayon réfracté est dit angle de réfraction.
Les angles i1 et i2 sont positifs si ils sont orientés dans le sens trigonométrique (sens inverse des aiguilles d'une montre), négatifs sinon.

La loi
On prend n1 l'indice de réfraction du milieu dans lequel se propage le rayon incident et n2 celui du milieu dans lequel se propage le rayon réfracté.
Pour pouvoir énoncer la loi de la réfraction, il faut que le rayon réfracté, le rayon incident et la normale (au dioptre) soient dans un même plan qui est appelé le plan d'incidence et que le rayon incident et le rayon réfracté soient situés de part et d'autre de la normale.
Lorsque n1 > n2 (et respectivement n1 < n2) le rayon réfracté (et respectivement : incident) se rapproche plus rapidement du dioptre que le rayon incident (ou réfracté). Cependant, il existe un cas particulier où le rayon réfracté (ou incident) se retrouve mathématiquement sur le dioptre (sa limite) : il y a alors réflexion totale.
Il faut d'abord connaître la longueur des rayons réfléchis. On utilise alors le théorème de Pythagore pour connaître la longueur de l’hypoténuse et donc la longueur des rayons :
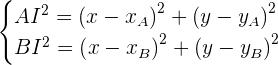
Rappel : D'après le théorème de Pythagore, le carré de la longueur de l’hypoténuse est égale à la somme des carrés des côtés adjacents à cette dernière.
Il faut ensuite poser les conditions de l'expérimentation :
Dans le milieu 1, l'onde se déplace à la vitesse c (vitesse de la lumière)
Dans le milieu 2, l'onde se déplace à la vitesse v avec : 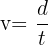
Il faut, dans un second temps, établir les temps de déplacement des ondes lumineuses avec :
t1 le temps de parcours dans l'air 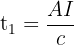
t2 le temps de parcours dans le milieu 2 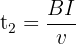
tAB le temps de parcours dans l'air mis l'onde pour aller de A à B
On a donc :

On doit maintenant déterminer l'abscisse x de telle sorte que tAB soit minimal.
On cherche donc à obtenir : 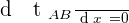

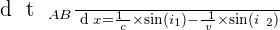
Or, pour obtenir ce que l'on cherche, il faut que :
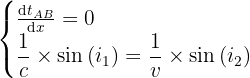
Ainsi, la formule de Snell-Descartes pour la réfraction est démontrée.
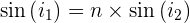
Les arcs en terre
Les arcs en terre, également appelés arc en ciel de rosée, correspondent à un phénomène optique très similaire à l'arc en ciel. Ceux-ci, très souvent de forme hyperbolique, sont formés grâce aux phénomènes de réfraction et de réflexion des rayons de soleil dans les gouttes de rosée.























Si vous désirez une aide personnalisée, contactez dès maintenant l’un de nos professeurs !
Merci pour cet article très complet :)