Sommaire :
- Que représente l'accélération ?
- Unité et notation
- Définition mathématique
- Vecteur accélération
- Déterminer l'accélération de la vitesse
- Déterminer l'accélération à partir d'un bilan de forces
- Déterminer l'accélération à partir d'un relevé de positions
- Accélération d'un corps en chute libre
- Expression d'une accélération en g
Que représente l'accélération ?
L'accélération indique comment évolue la vitesse d'un système au cour du temps.
- Si l'accélération est positive alors la vitesse augmente (le mouvement est dit accéléré) et cette augmentation est d'autant plus rapide que l'accélération est élevée.
- Si l'accélération est négative alors la vitesse diminue (le mouvement est dit ralenti ou déceléré) et cette diminution est d'autant plus rapide que l'accélération est en valeur absolue élevée.
- Si l'accélération est nulle alors la vitesse reste constante (le mouvement est dit uniforme)
Unité et notation
L'accélération se note en générale avec la lettre "a" (toujours en minuscule), elle s'exprime en mètre par seconde au carré dont le symbole est m/s 2 ou m.s -2 .
Définition mathématique
L'accélération instantanée d'un systéme est définie comme la dérivée de la vitesse par rapport au temps :
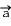 = = | d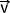 |
| ________________ | |
| dt |
Vecteur accélération
Tout comme la vitesse et la position, l'accélération peut être associée à un vecteur ayant même sens, même direction qu'elle et dont la norme correspond à sa valeur. Ce vecteur accélération est défini comme étant la dérivée du vecteur vitesse par rapport au temps:
| | d |
| ________________ | |
| dt |
Dans un repère orthonormé (O; 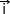
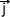
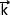
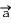
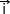
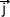
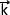
Etant donné que l'accélération correspond à la norme du vecteur accélération elle peut être calculée à l'aide de la relation:
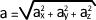
Ces composantes sont elles-même les dérivées des composantes la vitesses:
|
|
|
La vitesse étant elle une dérivée du vecteur position, les composantes du vecteur accélération peuvent s'exprimer sous forme de dérivées seconde des coordonnées du système:
|
|
|
Déterminer l'accélération d'un système à partir de sa vitesse
Si l'expression de la vitesse d'un système au cours du temps est connue alors il est possible d'en déduire la valeur de l'accélération.
Exemples simples:
- Si la vitesse est constante:
| a = | dv | or la dérivée d'une constante à une valeur nulle donc a = 0 m/s2 |
| ________________ | ||
| dt |
L'accélération est donc nulle
- Si la vitesse croit linéairement au cours du temps:
La vitesse peut alors s'exprimer sous la forme v = bt + c où b et c sont des constantes
| a = | dv |
| ________________ | |
| dt |
| a = | d(bt) | + | d(c) |
| ________________ | ________________ | ||
| dt | dt |
a = b + 0
a = b
Dans ce cas l'accélération est constante
Déterminer l'accélération d'un système à partir d'un bilan de forces
La seconde loi de Newton (aussi appelée relation fondamentale de la dynamique) établit une relation entre l'accélération d'un système et les forces externes auxquelles il est soumis:
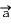
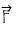
On en déduit la valeur de l'accélération:
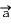
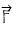
En général, pour exploiter cette relation, on utilise la méthode suivante:
- Effectuer un bilan des forces exercées sur le système
- Déterminer la valeur des différentes forces
- Déterminer la valeur des composantes des différentes forces suivant les axes du repère choisi.
- Utiliser la seconde loi de Newton pour exprimer la valeur de chacune des composantes:
a x = (1/m) x ΣF x ; a y = (1/m) x ΣF y ; a z = (1/m) x ΣF z
- La valeur de l'accélération totale peut enfin être calculée, elle correspond à la norme du vecteur accélération et peut donc être obtenue grâce à la relation 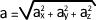
Déterminer l'accélération à partir d'un relevé de positions
Lorsque les positions d'un point sont relevées à intervalles de temps réguliers (notés ici τ ) sur alors il est possible de déterminer graphiquement le vecteur accélération en suivant la méthode suivante pour le point numéro "n" noté An:
- Déterminer le vecteur vitesse pour les deux points qui l'encadrent c'est à dire au point An-1 (point précédent) et An+1 (point suivant). Ces vecteurs vitesse sont alors notés respectivement Vn-1 et Vn+1.
- Tracer, en prenant comme origine le point An le vecteur Vecteur résultant 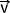
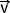
- Mesurer la norme du vecteur vecteur résultant 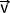
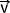
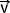
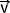
Exemple du tracé du vecteur accélération au point n°3 d'un relevé de positions d'un mobile par différence des vecteur vitesses des points 2 et 4
Accélération d'un corps en chute libre dans le champs de pesanteur terrestre
Un corps est dit en "chute libre" s'il chute sous l'effet de son poids en l'absence de tout autre force (en particulier en négligeant les frottements de l'air).
Dans ce cas la seconde loi de Newton permet d'obtenir la relation:
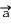 = = | 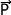 |
| ________________ | |
| m |
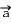 = = | m x 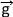 |
| _______________________ | |
| m |
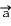
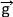
Si dans le repère choisi l'axe verticale est orienté vers le haut alors a = ay = -g
L'accélération du système possède une valeur égale en valeur absolue à l'intensité de la pesanteur.
Expression d'une accélération en g
Le paragraphe précédent montre que l'intensité de la pensanteur "g" correspond aussi à l'accélération d'un corps en chute libre , c'est pour cette raison que g est aussi appelé "accélération de la pesanteur" et qu'il est parfois utilisé comme référence pour exprimer d'autres accélérations. Ainsi une accélération de "deux g" est une accélération deux fois plus grande que celle possèdée par un corps en chute libre, "Trois g" est une accélération trois fois plus grande etc.












Si vous désirez une aide personnalisée, contactez dès maintenant l’un de nos professeurs !
C’est tres merveilleux ça
Salut j’aimerais faire une comparaison entre g et l’accélération suivant l’axe Y d’une machine sur une période T , j’ai utilisé un logiciel de simulation pour déterminer la courbe de cette accélération sur la période, mais je ne sais pas comment déterminer la valeur de l’accélération pour faire la comparaison avec g. quelle donnée utilisé pour faire cette comparaison ? Comparé en utilisant le RMS ? Ou avec la valeur moyenne ? Quelqu’un peut m’aider ?
C’est gentil
Je n’y comprends rien
C’est dur comme du pénis
Je suis vraiment satisfait de cet article. Je vous remercie beaucoup.
Salut s’il vous plait j’ai besoin de toutes les formules possible concernant la 3eme loi de kepler.