Chapitres
La diffraction est une modification de la direction de propagation d’une onde lors de sa rencontre avec un obstacle ou une ouverture de petite dimension.
? En 1801, le savant anglais Thomas Young explique la coloration des lames minces par un phénomène d’interférences, par analogie avec les interférences avec des ondes sonores. Il apporte la justification expérimentale de la nature ondulatoire de la lumière en 1807 en présentant l’expérience qui porte désormais son nom : “les trous d’Young”.
Cela a mené à étudier la diffraction lumineuse : on vous en dit plus ici !

Comprendre le lien entre lumière et reflet ?

La propagation de la lumière
? Voici quelques principes importants à retenir :
- Propagation possible dans le vide, c'est à dire sans support matériel.
- Vitesse c = 300 000 km/s dans le vide dans tous les référentiels. (En contradiction avec la loi de composition des vitesses de la mécanique classique.)
- Vitesse c/n dans un milieu transparent d'indice n.
- Attention : l'indice d'un milieu dépend de la longueur d'onde de l'onde qui se propage (milieu dispersif). En effet, c'est ce qui explique qu'un prisme en verre puisse décomposer un spectre lumineux.
- L'indice d'un milieu est supérieur à 1, donc la vitesse de propagation dans ce milieu inférieure à c.
- L'indice d'un verre est une fonction (légèrement) décroissante de la longueur d'onde : Le bleu est plus dévié que le rouge par un prisme.
- La propagation de la lumière émise par une source ponctuelle dans l'espace peut être décrite par les rayons lumineux ou les surfaces d'onde.
- L’utilisation des rayons lumineux est privilégiée en optique géométrique.
- L'utilisation des surfaces d'onde est privilégiée en optique ondulatoire.
- Les rayons lumineux sont les normales aux surfaces d'onde.
- Une surface d'onde est une surface dont les points ont été atteints par l'onde au même instant, par exemple :
- Une onde émise par une source ponctuelle dans un espace homogène est dite "sphérique" car les surfaces d'onde sont sphériques. Les rayons lumineux sont donc des droites passant par la source.
- Une onde plane à des surfaces d'onde planes, donc des rayons lumineux rectilignes tous parallèles entre eux.
- Une onde sphérique émise par une source ponctuelle a quasiment la structure d’une onde plane à grande distance de la source : on dit que localement l'onde est quasi-plane.
- La durée de propagation d'une onde de la source S à un point M dans un milieu homogène d'indice n est égale à SM/v = n.SM/c
- La durée de propagation d'une onde de la source S à un point M dans un milieu quelconque est égale à (SM)/c où (SM) est le chemin optique le long du rayon lumineux allant de S à M.
- On peut donc définir une surface d'onde relative à une source ponctuelle S comme une surface d'égal chemin optique depuis la source, c'est à dire l'ensemble des points M tels que (SM)=cte.
Une onde se propage dans un milieu qui le lui permet car la propagation résulte de la mise en mouvement d’une particule dans le temps mais aussi dans l’espace par rapport au milieu. Cela est possible uniquement si la source est dans un état vibratoire. On peut caractériser la propagation d’une onde par sa vitesse de propagation à l’aide la formule suivante :
\[ c = \lambda \times f \]
Avec :
- c la célérité de l’onde ;
- λ la longueur d’onde ;
- f la fréquence de l’onde.
⚡️ La vitesse de la lumière est de 300 000 km.s-1 et la célérité d’une onde sonore est de 344 m.s-1 La fréquence d'une onde ne dépend que de la fréquence de la source mais ne dépend pas de la fréquence de l'onde. La célérité d'une onde v dépend du milieu de propagation.
- Elle est toujours inférieure à celle de cette onde dans le vide c . v < c .
- n est toujours inférieur à 1 . n < 1
Dans le vide, la célérité de la lumière est c = 299 792 458 m.s-1 (on retiendra c = 3.108 m.s-1). La célérité de la lumière dans le vide ne dépend pas de la fréquence de l'onde. La célérité de la lumière dans l'air est pratiquement égale à sa célérité dans le vide.
Les deux types de diviseurs d’ondes
On distingue :
- Diviseur du front d'ondes : Une division géométrique du faisceau émis par la source primaire. Exemples : trous et fentes d'Young, miroirs de Fresnel, miroir de Llyod...
- Diviseur d'amplitude : Une séparation de l'énergie du faisceau émis par la source primaire à l'aide d'une lame semi-réfléchissante.
Les conditions de diffraction d'une onde ?

? La diffraction peut se produire aussi bien sur :
- Des ondes mécaniques (ondes sonores, déformations de la surface de l'eau)
- Des ondes électromagnétiques.
Elle se produit lorsque :
- L'onde rencontre un obstacle qui peut être un objet matériel (cheveu, poussière, fil, etc.) ou une ouverture dans une surface (fente, trou, etc.).
- L'obstacle rencontré a une dimension qui est du même ordre que la longueur d'onde
Plus la taille de l’obstacle est petite face à la longueur d’onde λ de l’onde considérée, plus la diffraction sera marquée.
Exemples :
- Une onde sonore de fréquence 440 Hz a une longueur d'onde :
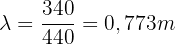
Cette onde est donc diffractée par des obstacles dont la dimension est de l'ordre de 80 cm - Une lumière visible rouge dont la longueur d'onde est de l'ordre de 800 nm est diffractée par des obstacles dont la dimension est de l'ordre de 800 nm.
Diffraction d'une onde mécanique
Après sa rencontre avec l'obstacle diffractant, la direction de propagation de l'onde est modifiée : elle se propage dans différentes directions avec un écart angulaire maximum noté θ par rapport à la direction de propagation initiale.
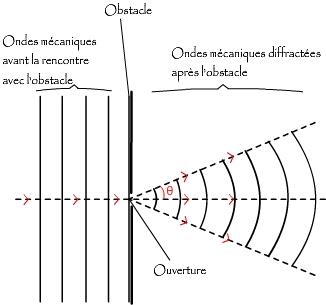
? L'angle θ, exprimé en radians (rad), dépend de la longueur d'onde et de la dimension de l'obstacle. Dans le cas d'une onde mécanique de longueur d'onde λ (m) rencontrant un obstacle avec une ouverture de largeur a (m), il existe la relation suivante :
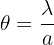
Remarque : l'angle obtenu à partir de la relation précédente s'exprime en radians, mais il est possible de le convertir en degré en utilisant la proportionnalité existant entre ces deux unités.
Étant donné qu'un angle de valeur π radians correspond à un angle de 180 degrés, alors :
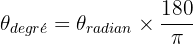
Diffraction d'une lumière monochromatique
Principe de l’interférence lumineuse
? L’énergie Ф(λ) d’un rayon lumineux monochromatique de fréquence f est formée de N photons, d’énergie hf.

Pour rappel :
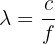
Si en un même point, 2 rayons lumineux de même longueur d’onde λ et de même amplitude se superposent, ils interfèrent. Il en est de même pour une seule source lumineuse passant à travers deux fentes étroites de largeur a << λ.
On observe alors une succession de :
- Maxima = franges brillantes → les interférences sont constructives, les ondes sont en phase, l’intensité lumineuse est maximale.
 ou multiple de 2π soit
ou multiple de 2π soit 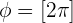
- Minima = franges sombres → les interférences sont destructives, les ondes sont en opposition de phase, l’intensité lumineuse est minimale

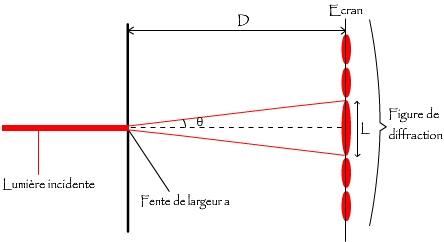
? Lorsqu'une lumière monochromatique rencontre un obstacle d'une dimension proche de sa longueur d'onde, la lumière diffractée se propage dans des directions qui différent de celle de la lumière incidente : on obtient une figure de diffraction formée de tâches lumineuses séparées de zones sombres.

Schéma : figure de diffraction obtenue avec une lumière monochromatique rouge et une fente
Prenons l’exemple d’une lumière monochromatique de longueur d’onde λ, qui traverse une fente réelle simple de largeur a (m) inférieure à λ. La figure de diffraction observée sera alors composée d’une large figure centrale (correspondant à un maximum), ainsi que des maxima secondaires moins intenses, le tout séparés par des minimas (correspondant aux « espaces » entre les franges brillantes).
Analyse d’une figure de diffraction
Dans le cas d'une lumière monochromatique diffractée par une fente de largeur a (m), on obtient sur un écran une tâche centrale limitée par des rayons diffractés dont le demi angle au sommet θ (rad) dépend de la largeur de la fente et de la longueur d'onde de la lumière λ (m).
Les interférences dépendent de la différence de marche ∆L. On obtient alors des :
- Franges brillantes :

- Franges sombres :
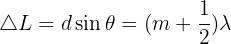 avec m = 0, ± 1, ± 2…
avec m = 0, ± 1, ± 2…
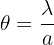
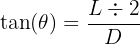
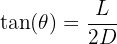

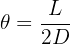
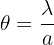
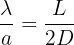
Cette relation permet :
- De calculer la longueur d'onde de la lumière :
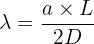
- De déterminer la largeur de la fente ou de l'obstacle responsable de la diffraction :
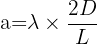
- De déterminer la distance entre la fente et l'écran :
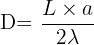
On peut déduire des relations précédemment évoquées que les tâches se rapprochent dans le cas où la longueur d’onde λ de la lumière incidente diminue. De même, plus la taille de la fente est importante, plus les taches se rapprochent.
Variation de l’intensité lumineuse d’une figure de diffraction
L’intensité lumineuse varie au sein d’une figure de diffraction selon les paramètres suivants :
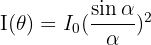 avec
avec 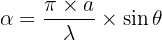
L’intensité est donc minimale lorsque alpha est un multiple de pi, soit a = n x pi. Elle est également proportionnelle à E0, l’énergie de l’état fondamental de l’atome d’hydrogène H égal à 13,6 eV.
Les minimas d’intensité sont observés pour des directions vérifiant :
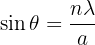
Dans cette formule, n est un nombre entier caractérisant l’ordre de diffraction. Plus l’ordre est élevé, plus l’intensité lumineuse est faible.
Processus de diffraction de la lumière blanche ☀️

La lumière blanche est une lumière polychromatique composée de toutes les lumières du visible.
Le spectre obtenu présente une tache centrale blanche, car elle correspond à la superposition de toutes les lumières colorées, ainsi que des taches latérales représentant le spectre des couleurs du visible, en miroir par rapport à la tache centrale.
Cela s’explique par le fait que les radiations se superposent au centre, mais présentent un décalage de plus en plus important plus on s’éloigne du centre.
Résumé du dispositif des fentes d'Young
? On appelle fentes, ou interférences, de Young toute expérience consistant à faire interférer deux faisceaux de lumière qui sont issus d'une même source. Cette interférence est produite grâce au passage de la lumière dans deux petits trous qui auront été percé au sein d'un plan opaque.
On observe alors pour résultat, sur un écran disposé face à ces fentes, un motif de diffraction représenté par une zone où des franges sombres et des franges illuminées sont disposées en alternance. Cette expérience permet ainsi de mettre en lumière la nature ondulatoire des ondes électromagnétiques.
⚛️ Lorsque cette même expérience est réalisée avec de la matière, comme des atomes, des molécules ou des électrons, il est possible d'observer ce même comportement. On peut ainsi observer la dualité onde-particule puisque les interférences permettent de montrer que la matière présente également un comportement ondulatoire bien que les impacts sur l'écran démontrent un comportement particulaire
Dispositif sans lentilles
- Description du dispositif : la source ponctuelle principale est constituée d'une lampe spectrale (plus filtre) et d'un petit diaphragme circulaire. Les sources secondaires sont créées grâce au phénomène de diffraction (voir plus loin).
- Détermination de la forme des franges : elles sont bien rectilignes. La différence de marche en tout point de l'écran ne dépend en effet que d'une seule variable.
- Détermination de l’interfrange : elle est égale au produit de la longueur d'onde par la distance de l'écran aux sources, divisé par la distance entre les deux sources. i=λD/a
- La position de la frange brillante d'ordre 0 est évidente pour un dispositif parfaitement symétrique.
- Si on admet que les franges sont rectilignes, on peut faire un calcul rapide pour retrouver l'interfrange et la position des franges.
Dispositif avec lentilles
- Description du dispositif : une lentille sert à éclairer les trous par une onde plane, une autre lentille sert à observer les interférences à l'infini.
- La présence de lentilles interdit le calcul de la différence de marche de façon purement géométrique car on ne connait pas les distances exactes parcourues dans la lentille.
Dispositif se ramenant aux trous d’Young : les miroirs de Fresnel
- Description du dispositif.
- Recherche des sources secondaires et analogie avec les trous d’Young.
- Calcul de l'écart entre les deux sources secondaires et de l’interfrange.
Sources lumineuses non ponctuelles et diviseurs d'onde
Position du problème
- Dans tout ce qui précède, on a fait l’hypothèse d'une source ponctuelle c'est à dire une source émettant une onde unique (dans la pratique, il s'agirait d'un atome seul).
- En réalité, une source même petite comporte plusieurs atomes donc émet plusieurs ondes.
- Qu'observe-t-on dans une expérience d'interférences à deux ondes avec une source non ponctuelle ? Deux atomes distincts émettant indépendamment l'un de l'autre avec un déphasage aléatoire, les ondes émises par chacun ne peuvent interférer. Il suffit donc d’additionner les intensités des figures d'interférence dues à chaque atome.
- Pour prévoir l'allure de la figure d'interférences avec une source non ponctuelle, il suffit de voir comment varie la figure d'interférence quand on passe d'un atome à l'autre.
Trous d’Young éclairés par une source monochromatique non ponctuelle
- Pour une source fente infiniment fine, perpendiculaire à l'axe des sources : chaque point source donne la même figure d'interférence. La figure d'interférence est donc la même que pour une source ponctuelle, mais plus lumineuse.
- Pour une source fente large, perpendiculaire à l’axe des sources : lorsqu'on passe d'une fente source fine à une fente source fine voisine, la figure d'interférence se translate car un déphasage est introduit entre les deux sources secondaires.
- Sans calculs :
- Le contraste va varier en fonction de la largeur de la fente source.
- Détermination de la largeur de fente qui annule le contraste.
- Calcul complet du contraste en fonction de la largeur de fente.
Fentes d’Young et réseau de diffraction
Le dispositif des fentes de Young consiste à éclairer deux fentes parallèles proches par un laser. Le faisceau incident se retrouve ainsi scindé en deux faisceaux lumineux, qui vont interférer l’un avec l’autre, créant ainsi une figure de diffraction alternant franges sombres et franches brillantes.

Lorsque le nombre de fentes est plus important, plus la taille du spectre augmente. En plaçant un grand nombre n de fentes devant une source lumineuse, on obtient donc un réseau de diffraction.
? Le réseau de diffraction est utilisé en analyse spectrale afin de déterminer les différentes espèces chimiques d’un composé par dispersion et diffraction de la lumière. Une lumière polychromatique donnera une figure de diffraction différente pour chaque longueur d’onde car l’interfrange (distance entre les taches de diffraction) est fonction de la longueur d’onde.
Cette capacité à distinguer les différentes raies du spectre sera d’autant plus importante que la résolution du réseau sera importante. La résolution R (sans unité) est dépendante de l’ordre de diffraction m et du nombre N de fentes éclairées dans le réseau. Elle est également équivalente au rapport entre la largeur du réseau et le pas (distance entre les fentes).

Pour aller plus loin : d'autres réactions de la lumière ?

Dispersion des ondes
? Un milieu est dispersif pour les ondes si la vitesse de propagation de l'onde dans le milieu dépend de sa fréquence de dispersion. Notez :
- L'air n'est pas un milieu dispersif pour les ondes sonores car les sons graves et aigus (leur fréquence) s'y propagent à la même vitesse
- L'eau est un milieu dispersif pour les ondes à la surface de l'eau
Le cas d'un milieu transparent
Un milieu transparent est caractérisé par son indice de réfraction. L'indice de réfraction d'un milieu transparent correspond au rapport entre la célérité d'une onde se propageant dans le vide et sa célérité dans le milieu considéré.
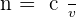 Avec
Avec
- n correspondant à l'indice de réfraction du milieu transparent et qui est une grandeur sans unité ;
- c correspondant à la célérité de l'onde dans le vide. La célérité est égale à 3.108 m.s-1 ;
- Et v correspondant à la célérité de l'onde dans le milieu transparent qui s'exprime en m.s-1.
Un milieu est dit dispersif si la célérité d'une onde lumineuse monochromatique qui se propage dans ce milieu dépend de sa fréquence (donc de sa longueur d'onde dans le vide). L'indice de réfraction d'un milieu dispersif dépend donc de la fréquence de l'onde qui s'y propage.
La réfraction de la lumière
☀️ La réfraction de la lumière correspond au changement de direction du rayon lumineux lorsque celui-ci traverse une surface séparant deux milieux d'indices de réfraction différents.
En effet, la loi de Snell-Descartes de la réfraction exprime le changement de direction d'un faisceau lumineux lors de la traversée d'une paroi qui sépare deux milieux différents. Il faut d'abord savoir que chaque milieu est caractérisé par sa capacité à « ralentir » la lumière. On modélise cette caractéristique par son indice de réfraction n qui s'exprime sous la forme :
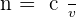
? Où v est la vitesse de la lumière dans ce milieu et c est la vitesse de la lumière dans le vide (souvent arrondie à 3.108 m.s-1 Il est important de savoir que :
- Le rayon lumineux est dit incident avant d'avoir rencontré la surface réfractante (appelée dioptre), il est dit réfracté après avoir rencontré cette dernière.
- Le point de rencontre du rayon incident et du dioptre est appelé point d'incidence.
- Le plan contenant le rayon incident et la normale au dioptre, au point d'incidence est dit plan d'incidence.
- L'angle orienté i1 pris entre la normale au point d'incidence et le rayon incident est dit angle d'incidence.
- L'angle orienté i2 pris entre la normale au point d'incidence et le rayon réfracté est dit angle de réfraction.
- Les angles i1 et i2 sont positifs s’ils sont orientés dans le sens trigonométrique (sens inverse des aiguilles d'une montre), négatifs sinon.
On prend n1 l'indice de réfraction du milieu dans lequel se propage le rayon incident et n2 celui du milieu dans lequel se propage le rayon réfracté. Pour pouvoir énoncer la loi de la réfraction, il faut que le rayon réfracté, le rayon incident et la normale (au dioptre) soient dans un même plan qui est appelé le plan d'incidence et que le rayon incident et le rayon réfracté soient situés de part et d'autre de la normale.
Lorsque n1 > n2 (et respectivement n1 < n2) le rayon réfracté (et respectivement : incident) se rapproche plus rapidement du dioptre que le rayon incident (ou réfracté). Cependant, il existe un cas particulier où le rayon réfracté (ou incident) se retrouve mathématiquement sur le dioptre (sa limite) : il y a alors réflexion totale.
La lumière peut être déviée par des molécules
Le pouvoir rotatoire
On appelle pouvoir rotatoire tout angle de déviation du plan de polarisation d'une lumière qui est polarisée rectilignement pour tout observateur qui va se situer en face du faisceau dit incident.
? Ce pouvoir rotatoire est alors lié à l'activité optique ou encore biréfringence circulaire correspondant alors à la propriété que peuvent présenter certains milieux que l'on considère comme étant optiquement actifs. Cette propriété consiste alors à la capacité de faire tourner le vecteur d'un faisceau lumineux qui va traverser le dit milieu optiquement actif.
Selon la direction dans laquelle les composés peuvent dévier le vecteur, ils portent un nom différent :
- On appelle composés dextrogyres, comme le saccharose, tout composé induisant une déviation du vecteur vers la droite lorsque l'observateur se situe face au faisceau ;
- Et on appelle composés lévrogyres, comme le fructose, tout composé induisant une déviation du vecteur vers la gauche lorsque l'observateur se situe face au faisceau ;
? Ce phénomène de rotation de la polarisation d'une lumière polarisée rectilignement a été observé pour la première fois au début du XIXe siècle par Jean-Baptiste Biot, d'où la loi de Biot, avant même que la nature des molécules ne soit comprise.
On a alors utilisé des polarimètres afin de mesurer la concentration de différents sucres, tels que le glucose, en solution. On a alors par moment associé le nom de ces sucres à leur effet. C'est notamment le cas du dextrose qui provoque une déviation de la polarisation vers la droite.
La loi de Biot
La loi de biot permet d'exprimer la proportionnalité du pouvoir rotatoire d'un milieu aux concentrations en produits optiquement actifs (dextrogyres ou lévogyres). Autrement dit, la loi de Biot permet, pour une solution et de par son pouvoir rotatoire, de mesurer sa concentration.
Elle s'exprime ainsi :
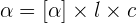
Avec :
- α correspondant au pouvoir rotatoire de la solution en degré (°) ;
- [ α ] correspondant au pouvoir rotatoire spécifique. A noter que cette valeur dépend de la température, de la longueur d'onde utilisée mais aussi du solvant. On utilise souvent dans les tables une valeur pour une température de 20°C ainsi que pour une longueur d'onde de la raie jaune du sodium à 589,3 nm.
- l correspondant à la longueur de la cuve en décimètre (dm) ;
- et c correspondant à la concentration de la solution en gramme par millilitre (g.mL-1)
? Ainsi, lorsque les molécules sont en présence d'un champ optique, elles présentent toutes une activité optique. Il est alors possible d'observer une rotation de la polarisation d'un faisceau lumineux lorsque celui-ci va traverser un milieu qui est lui-même soumis à un champ magnétique. On appelle alors ce phénomène l'effet Faraday. Il constitue alors l'une des première constatation du lien existant entre la lumière et l'électromagnétisme.
Résumer avec l'IA :























Si vous désirez une aide personnalisée, contactez dès maintenant l’un de nos professeurs !
Cet article est très intéressant
thanks
Salut. J’espère que vous allez bien. Excusez-moi je voulais savoir pourquoi dans la formule de l’onde diffractée wt est souvent négligée
Bonjour, nous serions ravis de vous aider ! Avez-vous essayé de contacter l’un de nos professeurs ? Excellente journée ! :)
Bonjour Yann, ton cours sur la diffraction est très bien mais il faut juste rectifier une petite erreur: un faisceau lumineux diffracte à partir d’une ouverture inférieure au millimètre.
Une figure de diffraction est mesurable pour a = 0,5 mm = 500 µm avec un laser rouge, ce qui est donc bien supérieur, à par exemple, la longueur d’onde du laser ( λ (R) = 650 nm = 0,65 µm ).
Je me souviens plus de la raison, mais c’est un fait expérimental. :-)
Amicalement
Nicolas
Bonjour,
J’aurais voulu savoir comment calculer le diaphragme à ne pas dépasser en photographie pour éviter la diffraction. Je viens d’apprendre à calculer l’ouverture effective pour un grandissement donnés N(M+1) – N=ouverture ; M=grandissement.
Merci par avance.
Cordialement.
Merci beaucoup pour ses explications! Tout est super clair! Bien joué merci!
J’aime ce cours comment y accéder ???
Salut. J’espère que vous allez bien. Excusez-moi je voulais savoir pourquoi dans la formule de l’onde diffractée wt est souvent négligée
Bonjour, que voulez-vous dire par là ? Vous y êtes déjà.
Bonne journée.