Chapitres
"Qu'est-ce qui rend un concert de rock électrisant ou une bibliothèque si paisible ?" La réponse réside dans un phénomène fascinant et omniprésent : l'intensité sonore. Les ondes sonores, ces vibrations invisibles de l'air, portent en elles une énergie qui façonne notre perception quotidienne du monde.
Les ondes sonores sont des vibrations de l'air qui se propagent sous forme d'ondes. L'intensité sonore est la mesure de la quantité d'énergie sonore transportée par ces ondes. Elle est exprimée en décibels (dB) et permet de déterminer le niveau sonore :
D'un environnement (aéroport, industrie, hôtel)
D'un équipement (de musique, accessoire)
Connaître l'intensité sonore est important pour protéger notre ouïe contre les dommages auditifs et pour réguler les niveaux de bruit dans notre environnement. Il est également important de comprendre les principes de base des ondes sonores pour pouvoir les manipuler et les utiliser de manière efficace, notamment dans le domaine de la musique, de la communication et de la médecine.

Le rôle des ondes sonores dans l'intensité sonore

L'onde de façon générale
Une onde est une déformation ou une vibration qui se propage dans un milieu défini. Il existe trois types différents d’ondes :
Mécanique
Électromagnétique
Gravitationnelle
- Mécanique : Les ondes magnétiques nécessitent une matière qui se déforme afin de se propager. Ce matériau a la capacité recouvrer son état initial grâce aux forces de restauration qui inversent la déformation.
- Électromagnétique : Les ondes électromagnétiques quant à elles n’ont pas besoin de support pour se déplacer : elles correspondent à des oscillations périodiques de champs électriques et magnétiques qui peuvent alors se déplacer dans le vide.
- Gravitationnelle : Les ondes gravitationnelles n’ont plus de support pour se déplacer puisque ce sont les déformations de la géométrie de l’espace-temps qui se propagent.
La perception humaine du son
Le son correspond à une vibration mécanique d'un fluide qui va alors se propager, grâce à la déformation élastique du fluide, en prenant la forme d'ondes longitudinales. L'être humain, mais également beaucoup d'animaux, peuvent ressentir cette vibration grâce au sens que nous appelons : l'ouïe.

Les ondes sonores audibles sont caractérisées par des fréquences allant de 20 Hz à 20 kHz, ce qui correspond à des longueurs d'onde allant de 0,017 m à 17 m.
La propagation d'une onde
Un onde se propage dans un milieu qui le lui permet car la propagation résulte de la mise en mouvement d’une particule dans le temps mais aussi dans l’espace par rapport au milieu. Cela est possible uniquement si la source est dans un état vibratoire. On peut caractériser la propagation d’une onde par sa vitesse de propagation à l’aide la formule suivante :  Avec :
Avec :
- c la célérité de l’onde ;
- λ la longueur d’onde ;
- f la fréquence de l’onde.
La vitesse de la lumière est de 300 000 km.s-1 et la célérité d’une onde sonore est de 344 m.s-1
La structure de l'oreille humaine
Oreille externe
Elle se compose du pavillon de l’oreille (qui aide à localiser les sources sonores) et du conduit auditif. Ce dernier se termine par le tympan, qui réagit aux variations de pression comme la membrane d’un microphone.
Oreille moyenne
Les vibrations du tympan sont amplifiées dans l’oreille moyenne, puis transmises à l’oreille interne par trois osselets (qui sont le marteau, l’enclume et l’étrier), les plus petits du squelette humain. Le marteau est relié au tympan et l’étrier à la « platine de l’étrier » qui transmet la vibration au liquide de la cochlée
Le tympan humain
Le tympan correspond à une membrane fibreuse qui va séparer l'oreille externe de l'oreille moyenne. Son rôle est de capter les vibrations provoquées par les sons qui parviennent dans le conduit auditif externe pour ensuite les transmettre à la chaîne ossiculaire.
Oreille interne
L’oreille interne abrite le limaçon (cochlée), de la taille d’un petit pois.
Rempli d’un liquide, celui-ci est partagé en deux dans le sens de la longueur par la membrane basilaire.
Cellules ciliées
Les sons font vibrer la membrane basilaire de manière sélective :
- Les plus aigus sont captés sur la partie antérieure
- Les graves pénètrent au fond du limaçon
Ce mode de fonctionnement est comparable à celui d’un analyseur de fréquence
La membrane basilaire est tapissée d’environ 5000 cellules ciliées, des capteurs qui transforment les vibrations sonores en impulsions électriques transmises aux nerfs auditifs.
Les cellules ciliées externes, au nombre de
jouent également un rôle important
Elles sont de véritables amplificateurs, elles permettent d’adapter la réaction de la membrane en fonction du signal à traiter.
La parfaite coordination de ces éléments autorise des performances extraordinaires :
- L’intensité acoustique correspondant au seuil d’audition est I0 = 1× 10−12W⋅m−2, celle correspondant au seuil de la douleur IS= 1 W⋅m−2 ;
- La gamme de fréquences allant de 20 Hz à 10 ou 20 kHz (selon l’âge) recouvre trois décades. À cela s’ajoute une excellente capacité de résolution, l’oreille distingue des signaux qui restent confus pour un analyseur sophistiqué, tels que la mélodie d’un instrument au sein d’un orchestre
- L'ouïe dispose également d’une capacité de localisation très développée, qui lui permet d’identifier la provenance d’un cliquetis dans l’air à 3° près
Les intensités sonores maximale et minimale chez l'humain
Toutes les ondes sonores ne sont pas perceptibles par l'oreille humaine. À l'inverse, des intensités sonores trop élevées peuvent être dangereuses.
L'oreille humaine peut en moyenne percevoir des sons ayant une intensité sonore supérieure à 10-12 W.m-2.
Cette intensité sonore minimale est notée I0 et appelée seuil d'audibilité.
Par ailleurs, un son dont l'intensité sonore est très forte peut provoquer une douleur, ainsi qu'une perte d'audition partielle ou totale : on estime en général que le seuil de douleur correspond à une valeur d'environ 10 W.m-2.
Aussi, l'exposition répétée à des ondes sonores d'intensité élevées mais inférieures aux intensités maximales, sans protections appropriées, peu également engendrer des dommages sur l'oreille humaine.
L'onde sonore : de la source jusqu'au récepteur
On distingue le parcours de propagation du son selon le milieu, qui peut être :
Compressible, comme les fluides (air)
Incompressible, comme d'autres fluides (eau) ou solides
Lorsque l'onde se propage dans un milieu fluide compressible, il est possible d'observer une variation de pression qui va alors se propager sous la forme d'une onde. L'air nous entourant étant un milieu fluide compressible, il est alors possible de ressentir ces ondes sous la forme de son que l'on perçoit grâce aux tympans.
Cependant, pour qu'elle soit perceptible, il faut que la variation de pression, parce que son amplitude est faible par rapport à la pression atmosphérique, soit suffisamment rapide et répétée.
Il est possible de considérer tout objet vibrant, tel qu'un instrument de musique ou encore un haut-parleur, comme étant une source sonore qui est donc, comme son nom l'indique, la source des vibrations de l'air.
La perturbation va alors se propager, même si les particules oscillent très peu (soit quelques micromètres autour d'une position stable), d'une façon analogue aux perturbations de l'eau lorsqu'une pierre y tombe.
Ainsi, la vibration va se propager au sein du solide comme dans les fluides. Il y aura de faibles oscillations autour de la position d'équilibre des atomes constituant le solide.
⛔️ La conséquence est alors une contrainte du matériau qui, équivalente à la pression dans un fluide, est très difficile à mesurer
C'est donc la rigidité du matériau qui permettra la transmission des ondes de contraintes transversales. Il peut être intéressant de noter que, la vitesse de propagation du son, également appelée célérité, varie selon différentes propriétés du milieu comme :
- La nature du milieu (solide, liquide)
- La température du milieu (élevée, basse)
- Et la pression du milieu (activité, statique)
Ainsi, dans un gaz parfait, on peut obtenir la vitesse de propagation d'une onde sonore avec la relation suivante :  Avec :
Avec :
- ρ correspondant à la masse volumique du gaz
- Et χS correspondant à la compressibilité isentropique du gaz
Il est également possible d'observer une diminution de la vitesse du son lorsque :
- La densité du gaz augmente, on appelle cela l'effet d'inertie
- La compressibilité du gaz, c'est-à-dire sa capacité à changer de volume selon la pression qu'il subit, augmente
Calculer la vitesse du son
Pour calculer la vitesse du son dont l'unité est, rappelons-le, le mètre par seconde, il est possible d'utiliser l'expression suivante :
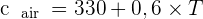 avec T la température en degré Celsius
avec T la température en degré Celsius
Mais il est possible d'être plus précis en utilisant les degrés Kelvin.
On doit alors se servir de l'expression suivante :
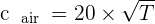
Notons que, de façon générale, la vitesse du son dans l'eau est de 1 500 m.s-1.
Mais il existe de nombreux milieux où les ondes sonores peuvent se propager de façon encore plus rapide. On peut alors prendre l'exemple de l'acier au sein duquel les ondes se propagent à une vitesse comprise entre 5 600 et 5 900 m.s-1.
Cependant, une onde sonore est incapable de se propager dans le vide puisqu'il faut nécessairement la présence de matière déformable pour que la vibration puisse se propager.

Comment fonctionne l'intensité sonore ?
Cette grandeur permet de donner une indication sur la "force" d'un son.
Plus l'intensité sonore est élevée et plus le son perçu est fort par l'oreille humaine
L'intensité sonore se note avec la lettre I et s'exprime en watt par mètre carré (W.m-2).
Cette unité indique qu'elle correspond à un "débit" d'énergie par unité de surface.
L'intensité sonore dépend de plusieurs paramètres :
- L'intensité sonore à l'émetteur
- La distance du récepteur à la source sonore
- La présence d'obstacles :
- Absorbants l'intensité sonore (double vitrage, mur antibruit)
- Réfléchissants les ondes (écho)
L'intensité sonore est captée par l'oreille externe et transmise par le tympan à l'oreille interne.
L'intensité sonore est captée par l'oreille externe et transmise par le tympan à l'oreille interne.
Intensité sonore totale de plusieurs ondes
L'intensité sonore est additive, c'est-à-dire que si plusieurs sources émettent des ondes sonores alors l'intensité sonore qui en résulte correspond à la somme des intensités sonores de toutes les sources.
Par exemple, si trois sources sonores émettent des ondes d'intensité I1, I2 et I3 en un point donné de l'espace alors, une mesure indiquerait que l'intensité sonore en ce point vaut :
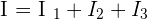
Le niveau d'intensité sonore : le Décibel

Le décibel, en acoustique environnementale, permet d'indiquer le niveau de bruit. En effet, cette grandeur permet d'exprimer le rapport de puissance existant enter la pression acoustique et une valeur de référence qui a été choisie comme correspondant à un son imperceptible.
D'une façon générale, le niveau sonore en champ libre, ce qui signifie sans obstacle sur le trajet de l'onde, est inversement proportionnel au carré de la distance, c'est-à-dire à la distance multipliée par elle-même.
| Rapport | dB |
|---|---|
| 1 | 0 |
| 1,12 | 1 |
| 1,26 | 2 |
| 1,4 | 3 |
| 1,6 | 4 |
| 1,8 | 5 |
| 2 | 6 |
| 2,2 | 7 |
| 2,5 | 8 |
| 2,8 | 9 |
| 3,2 | 10 |
| 4 | 12 |
| 5 | 14 |
| 6,3 | 16 |
| 8 | 18 |
| 10 | 20 |
| 18 | 25 |
| 32 | 50 |
| 100 | 40 |
| 320 | 50 |
L'intensité sonore perceptible prend des valeurs sur un intervalle extrêmement large qui va de 10-12 W.m-2 jusqu'à 10 W.m-2 soit un facteur de 1013 (10 000 milliards !) entre la limite inférieure et la limite supérieure.
Afin d'utiliser une échelle de grandeur plus simple et plus significative, on définit le niveau d'intensité sonore de la manière suivante.
Cette grandeur se note L, s'exprime en décibel de symbole dB et se calcule à partir de la relation suivante :
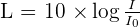
- Avec L en Décibel (dB)
- I en W.m-2
- I0 = 10-12 W.m-2
La relation entre l'intensité sonore et le niveau sonore en décibel est donc régi par une loi logarithmique, en conséquence deux choses.
☝️ Si l'on double l'intensité sonore, le niveau d'intensité sonore n'est pas doublé.
En effet : 
donc d'après les règles opératoires des logarithmes
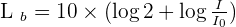
d'où
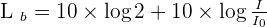 ]
]
soit
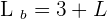 .
.
En conséquence, doubler l'intensité sonore revient à augmenter le niveau sonore de 3 décibels.
✌️ Même remarque si l'on divise par deux l'intensité sonore, le niveau de l'intensité sonore baisse de 3 décibels.
Remarque : Log correspond à la fonction logarithme décimale qui est définie à partir du logarithme népérien :
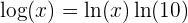
Niveau d'intensité sonore correspondant au seuil d'audibilité et au seuil de douleur
Nous connaissons les intensités sonores composant la gamme des sons audibles par l'humain. Afin de connaître cette gamme en décibels, le calcul suivant est effectué :
- Le seuil d'audibilité correspond à l'intensité sonore I0 = 10-12 W.m-2:
- sachant que
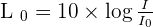
- donc
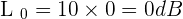
- sachant que
- Le seuil de douleur correspond à l'intensité sonore I0 = 10 W.m-2, donc
Le niveau d'intensité sonore d'un son audible par l'oreille humaine est donc compris entre 0 et 130 dB.

Calculer l'intensité sonore à partir du niveau d'intensité
A l'inverse, si l'on a mesuré le niveau sonore en décibels et que l'on souhaite connaître l'intensité sonore, on utilise la relation entre intensité sonore et niveau d'intensité sonore : 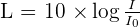
d'où

Il est alors nécessaire d'utiliser une propriété de la fonction logarithme qui est d'avoir comme fonction réciproque la fonction puissance de 10, c'est-à-dire qui si y = Log ( x ) alors x = 10y .
On en déduit donc la relation suivante :

d'où
Atténuation de l'intensité sonore avec la distance à l'émetteur
Le niveau de l'intensité sonore est dépendant de la distance à la source. Plus on s'en éloigne, moins le niveau sonore est intense. En effet, l'on "perd" 6 décibels lorsque l'on double la distance à la source.
C'est l'objet de nombreuses discussions pour les transports ferroviaires ou les villes à proximité de grands axes routiers.

La pression acoustique
La pression acoustique correspond à une grandeur physique qui stimule l'audition humaine. La plage de pression qui donne un niveau sonore perceptible par l'être humain est compris entre un rapport d'un et plusieurs millions.
Attention cependant, la perception du volume sonore est, de façon approximative, logarithmique.
⚠️ Cela signifie alors qu'une augmentation définie du volume correspondra à multiplier la pression par un facteur qui est identique
C'est pourquoi on ne convertit que très rarement la mesure du bruit, qui est de façon générale, correspondant à la pression acoustique en décibels.
L'intensité acoustique
Afin de déterminer les chemins de propagation des sons dans un environnement, les études acoustiques utilisent fréquemment l'intensité acoustique.
Cette grandeur correspond à la représentation de la puissance acoustique qui est transmise dans une direction définie
S'établissant généralement à partir d'un gradient de pression, on utilise logiquement un réseau de capteurs ou encore en ensemble de capteurs de vitesse acoustiques que l'on couple à un capteur de pression. Attention toutefois aux confusions :
❌ Parler d'une intensité acoustique n'induit pas toujours que l'on parle d'un niveau sonore
Exemple. Il suffit pour démontrer cela de prendre l'exemple d'une onde stationnaire. Son intensité est nulle alors que la pression acoustique ne l'est pas et l'on entend pourtant un son.
Une onde dite stationnaire correspond à la propagation simultanée et dans des sens opposés de plusieurs ondes de même fréquence et de même amplitude dans un même milieu. Ainsi, on observera une figure dont certains points sont fixes, appelés nœuds de pression, dans le temps. Il est alors possible d’observer une vibration stationnaire et d’intensité différente en chaque point observé au lieu de pouvoir observer une onde qui se propage.
La puissance acoustique
Afin de comparer deux sources de bruit, il est nécessaire d'utiliser la puissance acoustique qui s'exprime en dB SWL.
Il est possible d'obtenir la valeur de cette grandeur en plaçant la source que l'on souhaite tester dans une chambre réverbérante afin que les sons soient mélangés dans toutes les directions.
Mais il est également possible d'obtenir cette valeur en effectuant une série de mesures tout autour de la source sonore à tester.
Interférences
Les interférences ont un impact sur l'intensité sonore. Ainsi, si :
- Les interférences sont constructives (ondes en phase) alors l'intensité sonore est augmentée
- Les interférences sont destructives (ondes en décalage de phase) alors l'intensité sonore est diminuée
C'est ce principe qui est utilisé pour les casques audio à réduction de bruit active
Si la réduction passive consiste en la protection des oreilles du bruit extérieur par du matériau isolant (coussinet qui n'est pas là que pour le confort de l'usagé).
La réduction active, quant à elle, utilise des interférences destructrices.
En effet, le casque possède des micros extérieurs qui captent les sons extérieurs. Le casque reproduit ensuite le même son, mais en décalage de phase, alors l'intensité sonore des bruits environnants est diminuée voire annulée.
Mesure et protection de l'intensité sonore

C'est un sonomètre qui permet de mesurer l'intensité sonore en un point donné. Cet appareil permet de mesurer le niveau de pression acoustique à l'aide d'un simple microphone. Le signal enregistré est ensuite restitué par l'appareil par une valeur en décibels, après différent traitement.
Il est fréquemment utilisé pour évaluer l'environnement sonore au travail et le niveau d'exposition des employés par :
La médecine du travail (médecins, représentants, spécialistes)
Des organismes spécialisés dans la gestion du bruit (bien-être des employés, optimisation industrielle...)
Environnement sonore
Nous sommes constamment exposés au bruit, à la maison, dans la rue, au travail. En effet, la télévision, la chaîne HiFi, les voitures, le métro, le tramway, les machines, tout cela créent un environnement bruyant. On parle même de pollution sonore dans certains cas.

La réglementation s'est adaptée au problème de pollution sonore, ainsi trois seuils ont été définis :
- Seuil de risque : 80 dB. En dessous de ce seuil, on considère que l'exposition du travailleur est sans risques, quelle que soit la durée. Au-delà, la durée d'exposition doit être évaluée afin de mesurer la nécessité de protections auditives ou adaptation du poste de travail.
- Seuil de danger : 85 dB. Si la durée d'exposition de l'employé à une telle intensité sonore est de 8h par jour, les protections auditives sont requises. Si possible, le poste de travail peut être adapté afin de baisser le niveau sonore perçu par le travailleur.
- Seuil de douleur : 120 dB. À partir de ce niveau sonore, les oreilles souffrent physiquement du bruit. Cependant, attention les dommages sur l'audition interviennent bien en amont de la douleur.
| Environnement | Repas familial/ TV | Bus | Train/RER | Bar | Cinéma | Piscine municipal | Tondeuse | Discothèque/ concert | Marteau piqueur |
|---|---|---|---|---|---|---|---|---|---|
| Niveau sonore en décibel | 65 | 68 | 70 | 75 | 80 | 85 | 90 | 105 | 110 |
On comprend alors pourquoi des bouchons d'oreilles sont aujourd'hui proposés à chaque concert !
Pour se protéger d'un environnement bruyant, il existe plusieurs possibilités :
Protections personnelles adaptées selon l'intensité sonore et la durée d'exposition : bouchons d'oreilles, casques antibruits
Adaptation de l'environnement en protégeant le lieu : double vitrage (jusqu'à 40 dB de réduction du bruit), murs antibruit
Dans les environnements industriels, il est parfois possible d'enfermer le bruit en dédiant des espaces clos à certaines machines
Pour les protections personnelles, cela doit également s'adapter à l'activité. En effet, dans certains cas, il est nécessaire, ou du moins souhaitable, de pouvoir continuer à entendre les personnes autour. C'est le cas :
- Des ouvriers de chantiers
- Des agents d'entretien
- Des techniciens travaillant en extérieur (y compris architectes)
Il existe des protections filtrant seulement certaines fréquences d'intensités élevées.
Pour aller plus loin : les instruments de musique et l'intensité sonore
Le battement

D'un point de vue physique, un battement est une modulation périodique d'un signal. Ce dernier est constitué d'une superposition de deux signaux de deux fréquences différentes mais proches.
En effet, l'oreille humaine ne peut entendre deux sons différents que si leurs fréquences sont au moins éloignées de 0,5 Hertz à 5 Hertz.
Pour que les battements soient audibles par l'oreille, il faut que plusieurs conditions soient réunies telles que :
- Le battement doit être assez rapide (si la période est supérieure à 5 secondes alors le battement ne s'entendra pas)
- Le battement ne doit pas être trop rapide sinon on pourra en distinguer les deux composantes
- Les deux intensités des deux ondes doivent être environ égales afin que l'une ne se superpose pas à l'autre et la masque
Les ondes mécaniques formées par les instruments de musique sont des ondes sinusoïdales. La fréquence de ces ondes définit la hauteur de la musique.
Ces ondes sont aussi périodiques.
Si l'on analyse de manière mathématique ces ondes musicales, on remarque que la somme de deux sinusoïdes est égale à la moyenne des fréquences de ces deux ondes sinusoïdales.
La période d'une onde musicale
La période d'une onde représente la durée d'une vibration complète, jusqu'au retour à la position initiale. Elle se note T et a une durée en secondes.
Avec T correspondant à la durée d'un motif de base (Rappel pour les conversions : 1 ms = 1 x 10-3 s).
La fréquence des ondes
La fréquence caractérise le nombre de vibrations en une seconde. Calculée en Hertz de symbole Hz, on l'obtient par le calcul suivant :
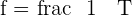
À titre d’exemple, la voix humaine produit des sons d'une fréquence allant de 50 Hz à 1000 Hz.
L'amplitude d'une onde
L'amplitude correspond à la variation de la pression du milieu dans lequel se propage l'onde dans le cas d'une onde acoustique. Pour une onde électromagnétique, son amplitude est sa tension maximale.
L'amplitude, c'est la tension maximale, elle se note Umax. Son unité est le Volt (V)
La longueur d'onde
La longueur d'onde est caractérisée par la plus petite distance entre deux points de l'onde situés au même endroit sur l'axe des ordonnées. Représentant la distance parcourue par l'onde durant sa période, il s'agit de son équivalent spatial.
Avez-vous encore des questions sur l'onde sonore et l'intensité sonore ? Posez-les en commentaires !

























Si vous désirez une aide personnalisée, contactez dès maintenant l’un de nos professeurs !
Cet article est très intéressant
Il y a une erreur, log (x) = ln(x) / ln(10) non pas ln(x) x ln(10)
Bonjour ! Merci pour cette rectification ! Bonne journée. :)
Bonjour, Pouvez-vous m’aider? Une sirène d’alarme a une puissance sonore de 100W. Calculer l’intensité sonore ressentie à une distance de 1 m de la source puis à 2 m de la source.
Bonjour, je vous recommande de prendre contact avec nos professeurs particuliers sur Superprof pour bénéficier d’un accompagnement personnalisé et approfondi, conçu pour répondre à vos besoins spécifiques. Très bonne journée à vous ! :)
Bravo
Bien
Je sollicite des sujets QCM et leur correction sur le document pour préparer mes concours de 2022
Merci cela m’a été très utile pour pouvoir préparer mon Grand Oral de Bac
Bonjour, nous espérons que vous avez réussi votre oral blanc :)
super ! cela m’a fait obtenir de nombreuses reponses