Chapitres

Définition de la cinématique
En physique, l'étude du mouvement d'objet ou d'un corps est appelée cinématique. Ce type d'étude ne s'intéresse qu'à la trajectoire et au temps de parcours (vitesse, accélération), mais pas aux causes du mouvement. Cette science allie la géométrie classique à la notion de temps.
L'étude de la cinématique a commencé au début du 18e siècle par Pierre Varignon, mathématicien français (1654-1722). Il définit alors le concept d'accélération et démontre que l'on peut calculer la vitesse instantanée d'un objet par calcul différentiel.
Les connaissances en cinématiques sont très utilisées aujourd'hui par les logiciels de modélisation, pour l'élaboration de machines complexes, mais sont également utilisées pour l'étude de la biomécanique (une partie de la biomécanique consiste en l'étude des mouvements du corps humain).

Le point matériel
L'étude d'un objet ou corps entier peut se révéler complexe. En effet, par exemple, si l'objet d'étude est grand ou large, alors les points de départ de leurs trajectoires respectives ne sont pas identiques. Aussi, si l'objet d'étude effectue également lui même des mouvements intrinsèques, les trajectoires de chaque point de l'objet pourraient être différentes. En cinématique du point, le corps est réduit en un point représentatif de l'objet. Le plus souvent c'est le centre de gravité de l'objet qui est choisi (point d'application des forces). Dans le cadre d'un objet plus complexe, avec des articulations par exemple, il peut être judicieux d'étudier également le mouvement au point de contact entre différentes parties de cet objet. Exemples :
- Dans le cadre de l'étude du mouvement d'une voiture : son centre de gravité est un point d'étude intéressant, tout comme un point appartenant au pneu d'une de ses roues.
- Dans le cadre de l'étude du mouvement de rotation d'une grande roue : le centre de gravité d'une nacelle est un point d'étude ainsi que le point de fixation de la nacelle sur la grande roue.
A noter que dans les deux cas, l'étude cinématique donnera des résultats différents au niveau de la trajectoire, de la vitesse et de l'accélération. Les référentiels d'études peuvent également être différents.
Notion de référentiel
L'étude du mouvement d'un objet et de l'expression de sa position, de sa vitesse ou de son accélération nécessitent au préalable le choix d'un référentiel. En effet, un passager dans un train est en mouvement par rapport aux rails mais pas par rapport au train. Un référentiel est un solide de référence défini par un point et trois axes pointant dans des directions fixes. La trajectoire décrite par l'objet en mouvement dépend du référentiel d'étude. Les référentiels les plus courants sont :
- Le référentiel terrestre associé à une portion de surface terrestre qui peut être choisi pour des mouvements de faible amplitude et de durée très faible par rapport à la période de rotation terrestre.
- Le référentiel géocentrique associé au centre de la Terre et trois axes pointant en direction d'étoiles fixes qui peut être utilisé pour étudier des mouvements de grande amplitude autour de la Terre mais dont la durée est négligeable devant la période de révolution terrestre.
- Le référentiel héliocentrique associé au centre du Soleil et trois axes pointant en direction d'étoiles pouvant être considérées comme fixes.
Pour illustrer la différence entre ces trois référentiels prenons l'exemple de la pyramide de Khéops :
- Elle est immobile depuis des siècles dans le référentiel terrestre.
- Elle décrit un mouvement circulaire uniforme dans le référentiel géocentrique de période 24 h.
- Elle décrit un mouvement de translation circulaire uniforme dans le référentiel héliocentrique de période 365.25 jours (c'est le 0.25 qui explique les années bissextile de 366 jours tout les 4 ans).
Exemple de référentiels terrestres : Reprenons la voiture :
- l'étude du mouvement de son centre de gravité est intéressant par rapport à la route.
- L'étude du point appartenant au pneu :
- peut se faire également par rapport à la route, et il s'agira d'étudier un mouvement circulaire associé à un mouvement rectiligne,
- ou par rapport à la voiture et seul le mouvement circulaire sera étudié.
L'importance du temps
Ce qui différencie la cinématique du point de la géométrie classique, c'est la prise en compte de la notion de temps. En effet la position, la vitesse et l'accélération sont dépendantes de l'évolution du mouvement donc du temps. Le temps devra donc est pris en compte pour la description de ces paramètres, d'autant plus lorsque le mouvement n'est pas uniforme. L'origine du mouvement est généralement appelée to.
Position et vecteur position
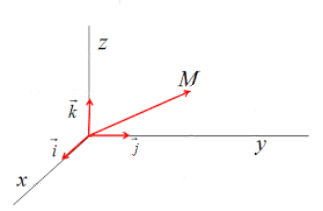
Dans un repère orthonormé, comme présenté ci-dessus, un point M est repéré par ses coordonnées (x, y, z). Il est également possible de définir le vecteur position qui peut s'exprimer en fonction de ces coordonnées et des vecteurs unitaires du repère : 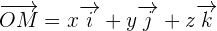 La norme de ce vecteur peut s'exprimer grâce à la relation suivante :
La norme de ce vecteur peut s'exprimer grâce à la relation suivante : 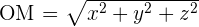 Remarque : si l'on étudie un mouvement se produisant dans un plan, alors les relations restent valables à condition de remplacer la coordonnée z par la valeur zéro.
Remarque : si l'on étudie un mouvement se produisant dans un plan, alors les relations restent valables à condition de remplacer la coordonnée z par la valeur zéro.
Le vecteur vitesse

Connaissant le vecteur position, il est alors possible de définir le vecteur vitesse. Ce dernier correspond à la dérivée du vecteur position par rapport au temps :  Cette relation peut également s'écrire sous la forme suivante :
Cette relation peut également s'écrire sous la forme suivante :  Dans cette relation :
Dans cette relation :
- la dérivée de X par rapport au temps correspond à la composante du vecteur vitesse selon l'axe des abscisses aussi notée vx.
- La dérivée de Y par rapport au temps correspond à la composante du vecteur vitesse selon l'axe des ordonnées aussi notée vy.
- La dérivée de Z par rapport au temps correspond à la composante du vecteur vitesse selon l'axe des cotes aussi notée vz.
On peut donc aussi noter cette relation de la manière suivante : 
Un objet en mouvement est aussi caractérisé par sa vitesse.
La vitesse est une grandeur physique qui est définie par une évolution face au temps.
La vitesse ne définit pas qu’uniquement la vitesse de déplacement mais peut aussi correspondre à la vitesse de réaction chimique ou encore une vitesse de séchage par exemple.
En règle générale, une vitesse est égale à la division de la mesure d’une variation telle qu’une longueur, un volume ou encore un poids par la mesure du temps écoulé au cours de cette variation.
L’exemple le plus simple est celui de la vitesse de déplacement. Il s’agit d’une distance divisée par un temps comme les mètres par seconde ou les kilomètres par heure.
Notion de vitesse moyenne : calculer une vitesse moyenne
La vitesse moyenne d’un point parcourant une distance d entre les instants t1 et t2 peut être calculée grâce à la relation suivante : 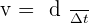
- où d est exprimée en mètre (m)
- Δt = t2 – t1 est exprimé en seconde (s )
- v est exprimé en mètre par seconde (m.s-1)
La valeur de la vitesse moyenne d’un mobile entre deux instants est donc le quotient de la longueur parcourue entre les deux instants par la durée du parcours. Il est possible d’utiliser d’autres combinaisons d’unités pour exprimer une vitesse à condition qu’elles soient cohérentes entre elles. Par exemple si le temps est en minute et la distance en kilomètre alors la vitesse est en kilomètre par minute (km.m-1)
Dans le système international (SI), la vitesse cinématique est le mètre par seconde et se note m/s ou m.s-1.
Or, dans le système usuel, on préférera, selon la situation et le mode de transport, le kilomètre par heure qui se note km/h ou km.h-1. En effet, dans la marine, on préférera plutôt le nœud, qui représente 0,5144 m/s.
On trouvera même dans certains cas, dans l'aviation par exemple, le nombre de Mach. Mach 1 est égale à la vitesse du son. Attention, cette vitesse dépend de la température.
Le système international des unités
L’ensemble des unités associées aux dimensions fondamentales constitue le système international d’unités. Il s’agit du système MksA (mètre, kilogramme, seconde, Ampère), mais le Kelvin, le mole et le candela font aussi partie de ce système. Ces unités sont appelées unités légales. Elles sont universelles et connues de par le monde entier.
Il est important de savoir que toutes les autres dimensions se déduisent de ces sept dimensions fondamentales par produit ou division de ces dimensions.
Dans certains sujets d’exercices, les grandeurs ne sont pas exprimées dans le système international mais avec des grandeurs usuelles. Il est facile de les comprendre et elles sont parfois utilisées dans la vie de tous les jours, mais il est essentiel de toujours effectuer les calculs avec les grandeurs exprimées dans l’unité internationale pour éviter les erreurs.
Calculer une distance ou une durée
Lorsque la vitesse est connue, cette expression peut être modifiée afin d’obtenir :
- La durée d’un trajet :
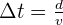
- La distance parcourue:
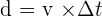
Convertir une vitesse
La formule qui exprime la vitesse peut également être utilisée pour convertir celle-ci... Pour passer d’une vitesse exprimée en kilomètre par heure à une vitesse en mètre par seconde. Si la vitesse a une valeur de v1 km.h-1 alors on peut considérer que cela correspond à une distance de v1 kilomètres parcourus en une heure.
- v1 km correspond à1000 x v1 m
- 1 heure correspond à 3600 s

- où v1 est une vitesse exprimée en kilomètre par heure
- v2 correspond à la même vitesse exprimée en mètre par seconde
En simplifiant on peut aussi écrire que v2 = v1 : 3,6 Par exemple si un point se déplace à une vitesse de 90 km.h-1 (90 x 1000)/3600 = 25 donc 90 km.h-1 correspond à 25 m.s-1. Pour passer d’une vitesse exprimée en mètre par seconde à une vitesse en kilomètre par heure. Si la vitesse a une valeur de v1 m.s-1 alors on peut considérer que cela correspond à une distance de v1 mètres parcourus en une seconde.
- v1 mètre correspond à v1/1000 kilomètre
- 1 seconde correspond à 1/3600 heure
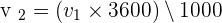
- v1 correspond à la même vitesse exprimée en mètre par seconde (m.s-1)
- v2 est une vitesse exprimée en kilomètre par heure (km.h-1)
En simplifiant on peut écrire v2 = v1 x 3,6 Par exemple si un point se déplace à une vitesse de 12,4 m.s-1 : (12,4 x 3600)/ 1000 = 44,64 donc 12,4 m.s-1 correspond à 44,64 km.h-1 .
| Vitesse en km/h | Vitesse en m/s |
|---|---|
| 90 km/h | 25 m/s |
| 120 km/h | 33 m/s |
| 130 km/h | 36 m/s |
Rappel concernant l'évolution de la vitesse au cours du temps
Au cours du temps les réactifs disparaissent donc leur concentration diminue. Or nous avons déjà vu que la concentration des réactifs est un facteur cinétique. Plus la concentration des réactifs est faible plus la réaction est lente. Donc, en général, au cours du temps la vitesse de réaction diminue.
- Si, pour un même intervalle de temps, la distance parcourue par le mobile est de plus en plus grande, sa vitesse augmente. On dit alors du mouvement qu'il est accéléré.
- Si, pour un même intervalle de temps, la distance parcourue par le mobile est constante. On dit que le mouvement est uniforme.
- Si, pour un même intervalle de temps, la distance parcourue est de plus en plus petite, sa vitesse diminue. On dit donc que le mouvement est ralenti.
La vitesse moyenne
La vitesse moyenne se calcule grâce au quotient de la distance L parcourue par la durée T mise à la parcourir. On a donc 
où la longueur de l’arc AB est notée L
La vitesse instantanée
La vitesse instantanée correspond à la vitesse du mobile à l’instant t. Elle peut être assimilé à la vitesse moyenne du mobile durant un intervalle de temps très court dt. On a donc 
Le vecteur vitesse 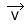
-
- sa direction : celle de la tangente à la trajectoire en M
- son sens : celui du mouvement
- sa valeur : valeur de la vitesse instantanée à l’instant t
- son origine : le point M
Notons qu'il est possible de la calculer grâce à la formule suivante 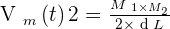
- Lors d'un mouvement rectiligne uniforme, le vecteur vitesse d’un point mobile est constant. Sa valeur, sa direction et son sens restent les mêmes à chaque instant..
- Lors d'un mouvement rectiligne varié, le vecteur vitesse garde la même direction mais les distances parcourues par le point mobile pendant des durées égales sont différentes.
- Une trajectoire correspond à un cercle dont le plan est orthogonal à l’axe fixe
- La vitesse angulaire moyenne se définit ainsi : Soit un point M décrivant une trajectoire circulaire de rayon R. Un rayon du cercle balaie un angle
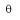
La vitesse angulaire moyenne peut se calculer grâce à l'expression suivante 
- La vitesse angulaire instantanée correspond à la vitesse angulaire à un instant donné. C’est le quotient du petit angle d θ balayé par un temps très court dt :
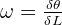 avec ω en rad/sd et θ en raddt en s
avec ω en rad/sd et θ en raddt en s
Il est tangent à la trajectoire au point considéré donc perpendiculaire au rayon. Son sens est celui du mouvement. Sa valeur est celle de la vitesse linéaire instantanée en ce point.
Le point M décrit un arc AB pendant la durée t. Le rayon OM = R balaie l’angle q. Donc l’arc AB est égal à rq.
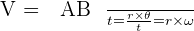
- La période, notée T, est l’intervalle de temps séparant 2 passages du mobile au même point et dans le même sens :
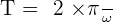 . La période s’exprime en seconde et la vitesse angulaire en rad/s
. La période s’exprime en seconde et la vitesse angulaire en rad/s - La fréquence, notée f, est le nombre de tours effectués par le mobile en une seconde :
 . La fréquence s’exprime en Hertz (Hz).
. La fréquence s’exprime en Hertz (Hz).
La vitesse moyenne d’un véhicule ne renseigne par sur le déroulement du trajet qui peut être jalonné de feux rouges, de ralentisseurs… Ainsi la vitesse moyenne ne donne qu’une information globale sur le trajet.
Afin de respecter les limitations de vitesse, le conducteur doit connaître la valeur de la vitesse instantanée (vitesse pour chaque instant t).
La vitesse instantanée d’un mobile à l’instant t est donc une vitesse moyenne pendant un temps très court. Cette vitesse est notée :
V = dL/dT
Le vecteur accélération
Nous pouvons maintenant définir le vecteur accélération sachant qu'il correspond à la dérivée du vecteur vitesse par rapport au temps :  Cette relation peut également s'écrire sous la forme suivante :
Cette relation peut également s'écrire sous la forme suivante : 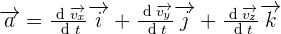 Dans cette relation :
Dans cette relation :
- la dérivée de vx par rapport au temps correspond à la composante du vecteur accélération selon l'axe des abscisses aussi notée ax.
- La dérivée de vy par rapport au temps correspond à la composante du vecteur accélération selon l'axe des ordonnées aussi notée ay.
- La dérivée de vz par rapport au temps correspond à la composante du vecteur accélération selon l'axe des cotes aussi notée az.
On peut donc aussi noter cette relation de la manière suivante : 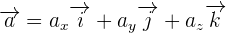
Accélération
L'accélération est le phénomène attenant à l'augmentation de la vitesse. L'accélération est égale à la dérivée de la vitesse instantanée. C'est à dire que la fonction dérivée de la fonction qui détermine la position d'un point selon le temps est l'accélération. Il s'agit d'une grandeur physique qui s'exprime sous la forme de vecteur. Comme la vitesse, il s'agit d'une variation au cours du temps. La norme de ce vecteur est l'accélération. Selon le système international, l'accélération a pour unité le mètre par seconde carré qui se note m.s-2.

Les débuts de cette notion
C'est en 1700 qu'un père jésuite français, Pierre Varignon, commence à identifier l'existence de l'accélération dans ces calculs. En effet, ce mathématicien a été l'un des premiers à chercher à comprendre le principe de la vitesse.
Approche graphique
Lors d'un courbe d'accélération, quand la vitesse est maximale, l'accélération est minimale.
Calculs
On peut effectuer différents calculs sur l'accélération. Voici ceux que vous pourriez être amenés à effectuer.
Accélération moyenne

Accélération instantanée

Les types de mouvements/trajectoires fréquent(e)s
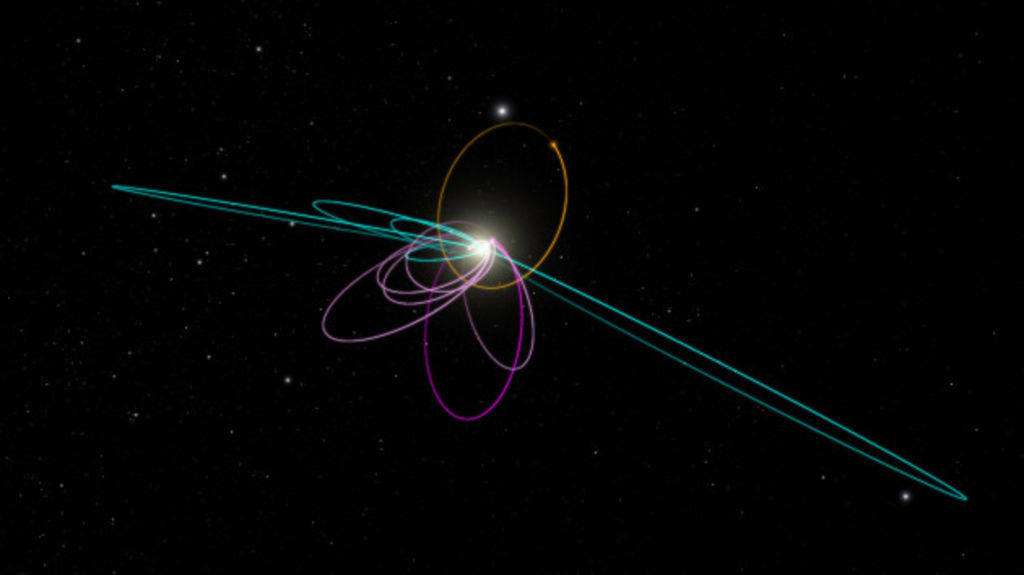
Les expressions des vecteurs position, vitesse, accélération dépendent du référentiel choisi et du type de mouvement dans ce référentiel.
Ces expressions des vecteurs position, vitesse et accélération sont générales et peuvent être appliquées aux différents types de mouvements classiques :
- rectiligne,
- circulaire,
- hélicoïdale (circulaire selon les axes x et y, et rectiligne selon z),
- elliptique...
Ces mouvements peuvent être uniformes ou variés. Pour des mouvements plus complexes, il pourront souvent être décomposer en plusieurs mouvements simples.
Pour étudier le mouvement d’un système on a toujours besoin de se fixer un référentiel : c’est un objet par rapport auquel on étudiera le mouvement de notre système.
Définition : La trajectoire d’un point matériel est l’ensemble des positions successives occupées par ce point au cours du temps. Elle dépend du référentiel choisi.
En simplifiant, on peut définir le référentiel comme quelque chose correspondant au milieu au sein duquel on étudie le mouvement.
En effet, si on choisi de prendre l'exemple du voyageur assit dans un train en marche alors le référentiel vas changer selon l'observateur :
- par rapport à un observateur sur le quai, le voyageur est en mouvement
- par rapport à un observateur dans le train, le voyageur est immobile.
Ainsi, il est possible de conclure que, pour décrire le mouvement d’un mobile, il faut choisir un repère d’espace ou référentiel.
Une trajectoire d’un point correspond à l’ensemble des positions occupées par ce dernier au cours de son mouvement. C’est une courbe. On distingue plusieurs types de trajectoire parmi lesquels les plus simples sont:
- La trajectoire rectiligne : ce qui correspond au fait que le mobile se déplace sur une droite. Le mouvement est d’ailleurs appelé mouvement rectiligne.
- La trajectoire circulaire qui correspond au fait que le mobile se déplace sur un arc de cercle. Le mouvement est appelé mouvement circulaire.
- Lorsque la trajectoire correspond à une courbe qui n’est pas un cercle on parle de trajectoire curviligne. Le mobile se déplace sur une courbe quelconque, plane ou non. Le mouvement est appelé curviligne.
Il existe aussi des trajectoires qui s’effectuent selon des figures géométriques plus complexes (comme par exemple les trajectoires hélicoïdales ou elliptiques).
Deux types de mouvement sont très importants dans l’étude des systèmes :
- la translation : Dans un mouvement de translation, chaque segment de droite, appartenant au mobile, reste parallèle à lui-même, au cours du déplacement et tous les points du mobile ont des trajectoires identiques de même longueur.
- la rotation : Dans un mouvement de rotation, tous les points du mobile décrivent des cercles ou des arcs de cercles centrés sur une droite fixe que l'on appelle axe de rotation. On peut notamment illustrer ce mouvement avec l'exemple des aiguilles d’une horloge.
- Si la trajectoire est une droite, la translation est rectiligne, comme dans le cas d'un ascenseur.
- Si la trajectoire est une courbe, la translation est curviligne, comme dans le cas d'un téléphérique.
- Si la trajectoire est un cercle ou un arc de cercle, la translation est circulaire, comme dans le cas d'une grande roue.
Définition : Une translation correspond à une droite passant par 2 points quelconques du solide qui reste parallèle au cours du mouvement
Définition :Une rotation correspond à un mouvement où tous les points décrivent des cercles dont les centres sont alignés et tous les plans sont parallèles.
Résumer avec l'IA :























Si vous désirez une aide personnalisée, contactez dès maintenant l’un de nos professeurs !
Je pense que ce serait mieux avec des exercices de compréhension. A l ‘appuie merci
Comment peut être observe la différence entre chacune trajectoire le vleche sur le type
Excellent
J’aime beaucoup lire vos pages parce que vous simplifier les cours
Merci pour votre commentaire :)
Ce site m’a vraiment aider.
Grâce à vos explications ,j’arrive maintenant à faire mes exercices sans dépendre de qui que ce soit. Merci c excellent
Trop cool le site merci super 👍 prof