Chapitres
- 01. Les énergies impliquées dans le mouvement
- 02. Condition pour qu'un mouvement rectiligne soit uniformément varié
- 03. Caractéristiques du vecteur accélération pour un mouvement rectiligne uniformément varié
- 04. Vitesse d'un point en mouvement uniformément varié
- 05. Position d'un point en mouvement uniformément varié
- 06. Résolution de problème en utilisant le mouvement rectiligne uniformément varié
- 07. Forces de frottement
- 08. Cas particulier de la chute libre
- 09. Mouvement rectiligne et inertie
- 10. L'inertie
- 11. Les mouvements et la vitesse
- 12. L'accélération
- 13. Les points d'actions permettant la naissance du mouvement

Les énergies impliquées dans le mouvement

L'énergie est un grandeur difficile à définir, on peut dire cependant que l'énergie caractérise l'état d'un système et exprime la potentialité à modifier l'état d'un autre système avec lequel il est en interaction. L'énergie peut alors se présenter sous différentes formes, dont :
- L'énergie cinétique : Tout corps en mouvement en possède une. Elle peut être macroscopique : elle dépend alors de la vitesse du corps en mouvement, et donc du référentiel d'étude microscopique : elle est liée à l'agitation moléculaire. Une augmentation de l'énergie cinétique microscopique se traduit par une augmentation de la température.
- L'énergie potentielle : Elle dépend de la position relative des différentes parties du système: seul un systèmes déformable pourra posséder, à l'échelle macroscopique, de l'énergie potentielle.
Condition pour qu'un mouvement rectiligne soit uniformément varié
De la même manière qu'un mouvement rectiligne uniforme, un mouvement rectiligne uniformément varié présente une trajectoire suivant une droite. Cependant, dans ce cas la vitesse n'est plus constante au cours du temps. Par contre la variation de sa vitesse est uniforme dans le temps.
Un mouvement rectiligne est uniformément varié si son vecteur accélération est constant en valeur en direction et en sens. 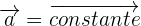
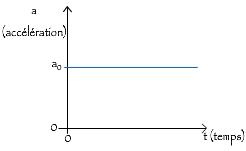
Caractéristiques du vecteur accélération pour un mouvement rectiligne uniformément varié
Le vecteur accélération est caractérisé par :
- sa norme constante et égale à l'accélération initiale à l'origine du mouvement : a=ao
- sa direction correspondant à celle du mouvement,
- son sens : si c'est le même que celui du mouvement (a>0) on parle de mouvement uniformément accéléré. S'il est opposé à celui du mouvement (a<0) on parle de mouvement uniformément ralenti.
A noter que l'accélération peu également s'exprimer de la manière suivante :
- l'accélération est la dérivée de la vitesse v en fonction du temps ce qui se traduit graphiquement par la relation suivante :
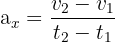
Vitesse d'un point en mouvement uniformément varié
Connaissant les caractéristiques du mouvement, il est alors possible de connaitre les coordonnées du vecteur vitesse dans le plan. Puisque le mouvement s'effectue selon une droite on peut choisir un repère dans lequel cette dernière coïncide avec l'axe des abscisses, ainsi le vecteur vitesse n'aura qu'un abscisse.
Puisque l'accélération correspond à la dérivée de la vitesse par rapport au temps, alors la vitesse est une primitive de l'accélération. L'accélération étant constante (a = a0) sa primitive est de la forme :  avec A une constante.
avec A une constante.
Déterminons alors la valeur de A :
à t=0 nous avons v=v0, donc 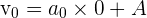 d'où
d'où 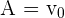
La constante A correspond donc à la vitesse initiale du point M à l'origine du mouvement.
La vitesse d'un point en mouvement uniformément accéléré est donc une fonction affine du temps de forme: 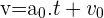
- où a0 et l'accélération à t=0
- vo est la vitesse à t=0
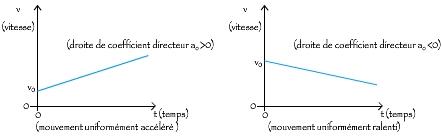
Remarques :
- Si la vitesse est nulle à t=0 alors la vitesse est une fonction linéaire du temps
- Si le mouvement est uniformément accéléré (a0>0) alors la vitesse est croissante au cours du temps.
- Si le mouvement est uniformément ralenti (a0<0) alors la vitesse est décroissante au cours du temps
Position d'un point en mouvement uniformément varié
Connaissant maintenant les coordonnées du vecteur vitesse dans le plan, il est alors possible de déterminer celle du vecteur position en fonction du temps.
Puisque la vitesse est une dérivée de la position par rapport au temps, alors la position est une primitive de la vitesse. Sa primitive est de la forme : 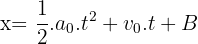 avec B une constante.
avec B une constante.
Il faut maintenant déterminer la constante B :
à t=0 nous avons x=x0, donc  d'où
d'où 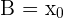
L'abscisse d'un point en mouvement uniformément accéléré est donc une fonction parabolique du temps de la forme: 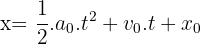
- avec ao accélération initiale à t=0
- vo vitesse initiale à t=0
- x0 abscisse initiale à t=0

Remarques :
- Si le déplacement est orientée dans le même sens que l'axe des abscisses alors l'abscisse du point M en fonction du temps est une fonction croissante.
- Si le déplacement est orientée dans le sens inverse de l'axe des abscisses alors l'abscisse du point M en fonction du temps est une fonction décroissante.
Résolution de problème en utilisant le mouvement rectiligne uniformément varié
Reprenons nos deux métros en mouvement rectiligne circulants en sens opposés entre les stations Louvres-Rivoli et Châtelet-les-halles séparées de 1 km.
On supposera que les rails du métro sont en ligne droite entre les deux stations.
Le métro 1 qui effectue le trajet dans le sens Louvres-Rivoli vers Châtelet est bondé et roule dans un mouvement décéléré uniforme de 15 km/h pour s'arrêter à châtelet 6 minutes plus tard.
Le métro 2 effectuant le trajet dans l'autre sens est vide et ne prends pas de voyageur, roule avec un mouvement uniformément accéléré de 0 à 35 km/h et atteint la station Louvres-Rivoli en 3,2 minutes.
A quelle distance de la station Louvres-Rivoli les trains vont-ils se croiser ?
De la même manière que pour le problème du mouvement rectiligne uniforme, nous allons utiliser les équations des positions en fonction du temps présentées ci-dessus :
- Appelons M1 le métro 1 d'abscisse x1 et M2 le méro 2 d'abscisse x2.
- Les équations des positions de M1 et M2 sont les suivantes :
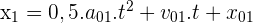
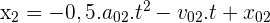 car M2 circule en sens opposé à l'axe des abscisses.
car M2 circule en sens opposé à l'axe des abscisses. - Les métro se croiseront pour x1= x2
- On obtient donc une équation avec cinq inconnus : t, a01, a02, x01 et x02. Cependant nous pouvons exprimer x02 en fonction de x01 car nous les savons distants de 1000 m :
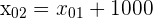 Nous choisissons x01 égale à 0 car c'est notre point de référence du mouvement.
Nous choisissons x01 égale à 0 car c'est notre point de référence du mouvement. - Nous pouvons calculer a01 :
- la vitesse initiale est de 15 km/h soit 4.2 m.s-2
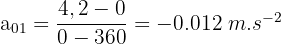
- Nous pouvons calculer a02 :
- la vitesse finale est de 35 km/h soit 9.7 m.s-2
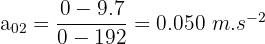
- On obtient donc l'équation suivante :
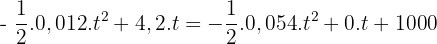 car x2 est dans le sens opposé au mouvement. Ceci donne l'équation du second degré suivante :
car x2 est dans le sens opposé au mouvement. Ceci donne l'équation du second degré suivante :  Cette équation a deux solutions mais une seule positive (un temps ne peut être négatif) d'où
Cette équation a deux solutions mais une seule positive (un temps ne peut être négatif) d'où  .
. - Les deux métros se croisent au bout de 140 s soit 2.3 min.
- Pour répondre à la question initiale, il suffit maintenant de connaitre x1 (ou x2 puisqu'ils sont identiques) :
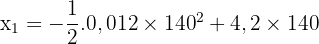
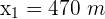
Les deux métros se croisent à 470 m de la station Louvres-Rivoli.
Forces de frottement

Lorsqu'un corps effectue un mouvement, il y a toujours des forces de frottement qui s'oppose à la vitesse et l'accélération (résistance de l'air, frictions sur la route ou les rails).
Ses forces de frottement augmentent avec l'accélération. Par exemple, plus une voiture va vite plus la résistance de l'air s'oppose au mouvement, plus il faut fournir de l'énergie pour maintenir une accélération constante.
Lors de résolution d'exercice les force de frottement sont souvent négligées car difficiles à appréhender.
Cas particulier de la chute libre
On appelle chute libre le mouvement que prend un objet sous la seule action de son poids.
Un tel mouvement ne peut avoir lieu que dans le vide.
On peut admettre que dans l’air, la chute est " libre " si l’on peut négliger :
- les frottements
- la poussée d’Archimède (il faut que la masse volumique de l’objet soit grande devant celle de l’air).
On a donc une variation du vecteur vitesse du centre d’inertie G de la bille : la valeur de la vitesse varie, la direction reste constante.
On peut monter que pour une hauteur de chute h ( en partant sans vitesse initiale), on a les deux relations suivantes ou v représente la vitesse : 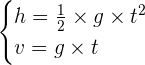
La poussée d’Archimède

La poussée d'Archimède est un phénomène physique qui décrit le comportement de tout corps plongé dans un fluide qu'il soit liquide ou gazeux soumis à un champ de gravité.
Elle est nommée ainsi en l'honneur d'Archimède de Syracuse, un très grand scientifique grec de 200 avant J.-C.
Elle est causée par l'augmentation de la pression du fluide avec la profondeur. Comme la pression exercée sur la partie basse du corps est supérieure à celle exercée sur la partie haute, le corps est poussé verticalement vers le haut.
Voici la formulation d'origine de cette loi physique :
Tout corps plongé dans un fluide au repos, entièrement mouillé par celui-ci ou traversant sa surface libre, subit une force verticale, dirigée de bas en haut et opposée au poids du volume de fluide déplacé ; cette force est appelée poussée d'Archimède.
Pour que le théorème s'applique il faut que le fluide immergeant et le corps immergé soient au repos. Il faut également qu'il soit possible de remplacer le corps immergé par du fluide immergeant sans rompre l'équilibre.
Voici l'équation qui en résulte :
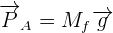
Avec :
- Mf< la masse du fluide contenu dans un volume V et déplacé ;
- g la valeur du champ de pesanteur, de 9,81 N/kg à la surface de la Terre.
Chute libre sans vitesse initiale
L'accélération
La chute libre est un excellent exemple de mouvement rectiligne uniformément accéléré. En effet, chaque objet sur terre, est soumis à la force d'attraction gravitationnelle.
Un objet en chute libre est soumis, quelle que soit sa masse, à une accélération de pesanteur que l'on peut considérer constante au voisinage de la Terre.
En négligeant les forces de frottement, cette accélération est de direction verticale, orientée vers le bas et sa norme, appelée g est exprimée de la manière suivante : 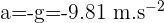 avec g la force gravitationnelle.
avec g la force gravitationnelle.
La vitesse
Nous avons démontré que la vitesse d'un mouvement rectiligne uniforme est de la forme : 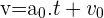 d'où dans le cas d'une chute libre sans vitesse initiale, nous obtenons :
d'où dans le cas d'une chute libre sans vitesse initiale, nous obtenons : 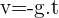 car vo est nulle.
car vo est nulle.
La position
Nous avons également l'expression de l'abscisse au cours du temps de la forme : 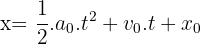 d'où dans le cas d'une chute libre sans vitesse initiale, nous obtenons :
d'où dans le cas d'une chute libre sans vitesse initiale, nous obtenons : 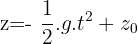 car vo est nulle et que le mouvement s'effectue le long de l'axe des ordonnées et non plus des abscisses.
car vo est nulle et que le mouvement s'effectue le long de l'axe des ordonnées et non plus des abscisses.
A noter que z peut aussi être appelé h (hauteur).
Paradoxe de la chute libre
Un caillou et une pierre de taille et de masses différentes lâchés en même temps sans vitesse initiale à 10 m de hauteur, frapperont le sol au même moment.
En effet, en réalité les forces de frottement ne sont pas négligeables. Si la pierre, plus grosse et plus lourde devrait avoir une accélération plus importante, sa résistance à l'air est également bien supérieure à celle du cailloux. Ces deux forces se compensant, la pierre et le cailloux ont la même vitesse.
L'exemple du BASE jump
Le BASE jump est une pratique de parachutisme qui consiste à sauter du haut d'une plateforme (parfois d'un pont ou d'une falaise) allant d'environ 50 à 1500 m, et de profiter de la chute libre la plus longue possible avant d'ouvrir son parachute.
Les BASE jumpers peuvent effectuer une chute libre au mouvement uniformément accéléré jusqu'à atteindre une vitesse maximale de 200 km/h (la résistance de l'air compense alors complètement l'accélération). Il a plusieurs morts chaque année lors de cette pratique, notamment en raison de mauvais calculs quant au moment d'ouverture du parachute.
Voici dans le tableau suivant quelques exemple de temps de chute en BASE jump en fonction de la hauteur de départ :
| Hauteur de saut (m) | 50 | 100 | 150 | 200 |
|---|---|---|---|---|
| Durée minimale de la chute (sans parachute) (s) | 3,2 | 4,5 | 5,5 | 6,4 |
| Vitesse maximal atteinte (m/s) Vitesse max 55.6 m/s | 31,3 | 44,3 | 54,3 | 55,6 |
La vitesse maximal est atteinte après un peu plus de 150 m de chute libre.
On remarque aussi que les temps de chute sont très court, c'est pourquoi il ne faut surtout pas ouvrir le parachute trop tard, sinon c'est l'accident assuré !
Mouvement rectiligne et inertie
L'inertie
En physique, on appelle inertie d'un corps, dans un référentiel galiléen, une tendance de ce corps à conserver sa vitesse. En effet, lorsqu'il y a absence d'influences extérieures, on parle aussi de forces extérieures, alors tout corps que l'on considère comme ponctuel va perdurer dans un mouvement rectiligne uniforme.
Notons que l'on appelle aussi l'inertie, principe d'inertie ou encore loi d'inertie. Puis, lorsque Newton est arrivé, on l'appelle également première loi de Newton.
Elle s'énonce ainsi :
Un système isolé ou pseudo-isolé initialement au repos ou en mouvement rectiligne uniforme demeure dans son état.
On appelle référentiel galiléen tout référentiel au sein duquel le principe d'inertie est vérifié.
Même s'il n'existe aucun référentiel galiléen au sens strict. Il est cependant possible de considérer certains référentiels usuels comme galiléen si certaines conditions sont vérifiée :
- Ainsi, le référentiel terrestre peut être considéré galiléen si on considère un mouvement dont la durée ne dépasse pas quelques minutes dans le but de s'affranchir du mouvement de rotation propre de la Terre.
- Le référentiel géocentrique peut également être considéré comme étant galiléen si on considère un mouvement dont la durée ne dépasse quelques heures dans le but de s'affranchir du mouvement de rotation de la Terre autour du Soleil.
- Le référentiel héliocentrique peut aussi être considéré comme étant galiléen car l'impact du mouvement de rotation du Soleil au sein de la galaxie est négligeable.
Les mouvements et la vitesse

La vitesse correspond à une grandeur physique qui est définie par une évolution face au temps.
La vitesse ne définit pas qu’uniquement la vitesse de déplacement mais peut aussi correspondre à la vitesse de réaction chimique ou encore une vitesse de séchage par exemple.
En règle générale, une vitesse est égale à la division de la mesure d’une variation telle qu’une longueur, un volume ou encore un poids par la mesure du temps écoulé au cours de cette variation.
L’exemple le plus simple est celui de la vitesse de déplacement. Il s’agit d’une distance divisée par un temps comme les mètres par seconde ou les kilomètres par heure.
Calculer la vitesse
La vitesse est une grandeur qui permet d'exprimer la distance parcourue par le mobile pendant l’unité de temps. La vitesse moyenne est égale au quotient de la distance parcourue par le mobile par la durée de son parcours soit :
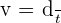 .
.
Avec :
- La vitesse v exprimée en mètre par seconde (m/s) ;
- la distance d exprimée en mètre (m) ;
- Et le temps t exprimé en seconde (s).
Dans le système international (SI), la vitesse cinématique est le mètre par seconde et se note m/s ou m.s-1.
Or, dans le système usuel, on préférera, selon la situation et le mode de transport, le kilomètre par heure qui se note km/h ou km.h-1. En effet, dans la marine, on préférera plutôt le nœud, qui représente 0,5144 m/s.
On trouvera même dans certains cas, dans l'aviation par exemple, le nombre de Mach. Mach 1 est égale à la vitesse du son. Attention, cette vitesse dépend de la température.
Les différents types de vitesse
Rappel concernant l'évolution de la vitesse au cours du temps
Au cours du temps les réactifs disparaissent donc leur concentration diminue. Or nous avons déjà vu que la concentration des réactifs est un facteur cinétique. Plus la concentration des réactifs est faible plus la réaction est lente. Donc, en général, au cours du temps la vitesse de réaction diminue.
- Si, pour un même intervalle de temps, la distance parcourue par le mobile est de plus en plus grande, sa vitesse augmente. On dit alors du mouvement qu'il est accéléré.
- Si, pour un même intervalle de temps, la distance parcourue par le mobile est constante. On dit que le mouvement est uniforme.
- Si, pour un même intervalle de temps, la distance parcourue est de plus en plus petite, sa vitesse diminue. On dit donc que le mouvement est ralenti.
La vitesse moyenne
La vitesse moyenne se calcule grâce au quotient de la distance L parcourue par la durée T mise à la parcourir. On a donc 
où la longueur de l’arc AB est notée L
La vitesse instantanée
La vitesse instantanée correspond à la vitesse du mobile à l’instant t. Elle peut être assimilé à la vitesse moyenne du mobile durant un intervalle de temps très court dt. On a donc 
Le vecteur vitesse 
-
- sa direction : celle de la tangente à la trajectoire en M
- son sens : celui du mouvement
- sa valeur : valeur de la vitesse instantanée à l’instant t
- son origine : le point M
Notons qu'il est possible de la calculer grâce à la formule suivante 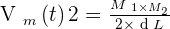
- Lors d'un mouvement rectiligne uniforme, le vecteur vitesse d’un point mobile est constant. Sa valeur, sa direction et son sens restent les mêmes à chaque instant..
- Lors d'un mouvement rectiligne varié, le vecteur vitesse garde la même direction mais les distances parcourues par le point mobile pendant des durées égales sont différentes.
- Une trajectoire correspond à un cercle dont le plan est orthogonal à l’axe fixe
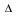
- La vitesse angulaire moyenne se définit ainsi : Soit un point M décrivant une trajectoire circulaire de rayon R. Un rayon du cercle balaie un angle
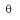
La vitesse angulaire moyenne peut se calculer grâce à l'expression suivante 
- La vitesse angulaire instantanée correspond à la vitesse angulaire à un instant donné. C’est le quotient du petit angle d θ balayé par un temps très court dt :
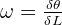 avec ω en rad/sd et θ en raddt en s
avec ω en rad/sd et θ en raddt en s
Il est tangent à la trajectoire au point considéré donc perpendiculaire au rayon. Son sens est celui du mouvement. Sa valeur est celle de la vitesse linéaire instantanée en ce point.
Le point M décrit un arc AB pendant la durée t. Le rayon OM = R balaie l’angle q. Donc l’arc AB est égal à rq.
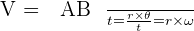
- La période, notée T, est l’intervalle de temps séparant 2 passages du mobile au même point et dans le même sens :
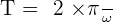 . La période s’exprime en seconde et la vitesse angulaire en rad/s
. La période s’exprime en seconde et la vitesse angulaire en rad/s - La fréquence, notée f, est le nombre de tours effectués par le mobile en une seconde :
 . La fréquence s’exprime en Hertz (Hz).
. La fréquence s’exprime en Hertz (Hz).
L'accélération
L'accélération correspond à un phénomène attenant à l'augmentation de la vitesse. L'accélération est égale à la dérivée de la vitesse instantanée. C'est à dire que la fonction dérivée de la fonction qui détermine la position d'un point selon le temps est l'accélération.
Il s'agit d'une grandeur physique qui s'exprime sous la forme de vecteur. Comme la vitesse, il s'agit d'une variation au cours du temps.
La norme de ce vecteur est l'accélération. Selon le système international, l'accélération a pour unité le mètre par seconde carré qui se note m.s-2.
Les débuts de cette notion
C'est en 1700 qu'un père jésuite français, Pierre Varignon, commence à identifier l'existence de l'accélération dans ces calculs. En effet, ce mathématicien a été l'un des premiers à chercher à comprendre le principe de la vitesse.
Approche graphique
Lors d'un courbe d'accélération, quand la vitesse est maximale, l'accélération est minimale.
Calculs
On peut effectuer différents calculs sur l'accélération. Voici ceux que vous pourriez être amenés à effectuer.
Accélération moyenne
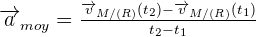
Accélération instantanée

Les points d'actions permettant la naissance du mouvement
Actions de contact localisées
Les actions de contact localisées correspondent à des actions qui s'exercent sur un point précis ou encore sur une petite surface du receveur comme dans le cas du perchiste et de sa perche ou encore dans le cas de la caravane tirée par une voiture.
Actions de contact réparties
Les actions de contact réparties correspondent à des actions qui s'exercent sur une grande surface du receveur comme dans le cas du le vent dans la voile ou dans le cas de l'eau sur la planche de surf.
Les actions à distance
On peut parler d'action à distance lorsque l'on se trouve dans un cas où il n'y a pas de contact entre l'acteur et le receveur et dans le cas ou ces actions se sont des actions réparties dans toute la matière de l'objet. Il existe alors différents types actions à distance :
- Les actions électriques comme dans le cas où fin filet d'eau attiré par une règle en plastique frottée avec de la laine, on parle alors d'électricité statiques causée par un champ ;
- Les actions magnétiques comme dans le cas où aimant attire les objets en fer et en nickel ;
- Ou encore les actions gravitationnelles qui s'exercent sur tous les corps dont la masse n'est pas nulle, on peut présenter l'exemple de l'attraction terrestre.
Il peut alors être intéressant de rappeler la définition des différents champs existant :
Le champ électrique
En physique, on appelle champ électrique tout champ vectoriel créé par des particules électriquement chargées. Plus exactement, lorsque nous sommes en présence d'une particule chargée, les propriétés locale de l'espace défini sont alors modifié ce qui permet de définir la notion de champ. En effet, si une autre charge se trouve être dans le dit champ, elle subira ce qu'on appelle l'action de la force électrique qui est exercée par la particule malgré la distance. On dit alors du champ électrique qu'il est le médiateur de la dite action à distance.
Si on se veut plus précis, on peut définir dans un référentiel galiléen défini, une charge q définie de vecteur vitesse v qui subit de la part des autres charges présentes, qu'elles soient fixes ou mobiles, une force qu'on définira de force de Lorentz. Cette force se décompose ainsi :
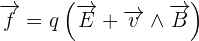
avec :
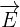 le champ électrique. Celui-ci décrit dans ce cas la partie de la force de Lorentz qui est indépendante de la vitesse de la charge
le champ électrique. Celui-ci décrit dans ce cas la partie de la force de Lorentz qui est indépendante de la vitesse de la charge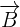 le champ magnétique. Celui-ci décrit ainsi la partie de la force exercée sur la charge qui dépend du déplacement de cette même charge dans le référentiel choisi.
le champ magnétique. Celui-ci décrit ainsi la partie de la force exercée sur la charge qui dépend du déplacement de cette même charge dans le référentiel choisi.
De plus, il est important de noter que les deux champs, électrique et magnétique, dépendent du référentiel d'étude.
Avec cette formule, on peut alors définir le champ électrique comme étant le champ traduisant l'action à distance subie par une charge électrique fixe dans un référentiel défini de la part de toutes les autres charges, qu'elles soient mobiles ou fixes.
Mais on peut également définir le champ électrique comme étant toute région de l'espace dans laquelle une charge est soumise à une force dite de Coulomb.
On commence à parler de champ électrostatique lorsque, dans un référentiel d'étude, les charges sont fixes. Notons d'ailleurs que le champ électrostatique ne correspond pas au champ électrique comme décrit plus haut dans cet article puisqu'en effet, lorsque les charges sont en mouvement dans un référentiel, il faut ajouter à ce référentiel un champ électrique qui est induit par les déplacement des charges afin d'obtenir un champ électrique complet.
Mais, le champ électrique reste dans la réalité un caractère relatif puisqu'il ne peut exister indépendamment du champ magnétique. En effet, si on observe la description correcte d'un champ électromagnétique, celui-ci fait intervenir un tenseur quadridimensionnel de champ électromagnétique dont les composantes temporelles correspondent alors à celle d'un champ électrique. Seul ce tenseur possède un sens physique. Alors, dans le cas d'un changement de référentiel, il est tout à fait possible de transformer un champ magnétique en champ électrique et inversement.
Le champ électromagnétique
En physique, on appelle champ électromagnétique la représentation dans l'espace d'une force électromagnétique exercée par des particules chargées. Ce champ représente alors l'ensemble des composantes de la force électromagnétique qui s'appliquent à une particule chargée qui se déplace alors dans un référentiel galiléen.
On peut alors définir la force subit par une particule de charge q et de vecteur vitesse par l'expression suivante :
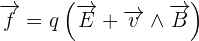
avec :
 le champ électrique. Celui-ci décrit dans ce cas la partie de la force de Lorentz qui est indépendante de la vitesse de la charge
le champ électrique. Celui-ci décrit dans ce cas la partie de la force de Lorentz qui est indépendante de la vitesse de la charge
 le champ magnétique. Celui-ci décrit ainsi la partie de la force exercée sur la charge qui dépend du déplacement de cette même charge dans le référentiel choisi.
le champ magnétique. Celui-ci décrit ainsi la partie de la force exercée sur la charge qui dépend du déplacement de cette même charge dans le référentiel choisi.
En effet la séparation de la partie magnétique et de la partie électrique ne dépend que du point de vue pris selon le référentiel d'étude.
De plus, il peut être intéressant de savoir que les équations de Maxwell régissent les deux composantes couplées, c'est à dire électrique et magnétique, de sorte que toute variation d'une composante induira la variation de l'autre composante.
D'ailleurs, le comportement des champs électromagnétiques se trouve décrit de façon classique par les équations de Maxwell et de manière plus générale par l'électrodynamique quantique.
La façon la plus utilisée afin de définir le champ électromagnétique est celle du tenseur électromagnétique de la relativité restreinte.
Le champ électrostatique
On parle de champ électrostatique lors que les charges qui constitue le champ sont au repos dans le référentiel d'étude. Ce champ est donc déduit de l'expression de la loi de Coulomb, aussi appelée interaction électrostatique.
Le champ gravitationnel
En physique classique, on appelle champ gravitationnel, ou encore champ de gravitation, un champ qui est réparti dans l'espace et dû à la présence d'une masse qui est alors susceptible d'exercer une influence gravitationnelle sur tout les autres corps pouvant être présent à proximité immédiate ou non.
On peut démontrer que le champ gravitationnel créé en un point quelconque par un corps ponctuel dérive d'un potentiel scalaire dit newtonien.
En physique classique, le champ gravitationnel ou champ de gravitation est un champ réparti dans l'espace et dû à la présence d'une masse susceptible d'exercer une influence gravitationnelle sur tout autre corps présent à proximité (immédiate ou pas). L'introduction de cette grandeur permet de s'affranchir du problème de la médiation de l'action à distance apparaissant dans l'expression de la force de gravitation universelle.
On peut interpréter le champ gravitationnel comme étant la modification de la métrique de l'espace-temps. L'approximation newtonienne est alors valable uniquement dans le cas où les corps présentent une vitesse faible par rapport à celle de la lumière dans le vide et si le potentiel gravitationnel qu'ils créent est tel que le quotient du potentiel gravitationnel sur le carré de la vitesse de la lumière dans le vide est négligeable.
On peut approcher le champ électrique et le champ gravitationnel. En effet, l'expression du champ et du potentiel ne sont différents que d'une constante. De plus, les principaux théorèmes de calculs, celui de la superposition ou de Gauss par exemple, peuvent s'appliquer dans les deux cas. Ce qui les différencie alors est le caractère attractif, donc entre deux charges de signe opposé, ou répulsif, donc entre deux charges de même signe, du champ électrique tandis que le champ gravitationnel ne peut être qu'attractif.
Résumer avec l'IA :























Si vous désirez une aide personnalisée, contactez dès maintenant l’un de nos professeurs !
Bonjour , j’ai envie d’approfondir mes connaissances en physique , chimie
Bonjour, nous serions ravis de vous aider ! Rendez-vous sur la plateforme de Superprof, sélectionnez la rubrique « Découvrir nos Superprofs » en indiquant les matières de physique et de chimie. Vous trouverez de nombreux professeurs près de chez vous. Excellente journée ! :)
On m a donné un exercice et je ne sais pas comment le résoudre
Bonjour je suis actuellement entrain de suivre la correction du problème (dans le chapitre MRUV) et je ne comprend pas pourquoi vous avez mis 180s dans votre corrigé alors que le temps été de 3,2minutes soit 3×6=180(+20secondes non?). Je ne comprend aussi pas votre calcul de a02 car il est dis dans le cours que a=(v2-v1)/(t2-t1) et dans l’exo le v2 n’est pas de 35km/h (soit 9,7m/s). Et pour finir je ne comprend pas vos conversion pour obtenir des km/h en m/s on divise par 3,6 (c’est ce que vous avez fait mais vous marquez dans votre correction que je résultat est en m/s^2
Je suis un passionné des physiques chimie mais j ai d inombrable lacune je souhaite approfondir mon savoir
Good
Bonjour ! Nous avons de nombreux professeurs qualifiés qui se feront une joie de vous aider !
Bonne journée
Avec plaisir
Ok moi aussi j’aime beaucoup la physique