Chapitres
- 01. Les mouvements rectilignes, qu'est-ce que c'est ? ?
- 02. Quelle est la condition pour qu'un mouvement rectiligne soit uniforme ? ?
- 03. Les caractéristiques du vecteur vitesse pour un mouvement rectiligne uniforme ➡️
- 04. Position d'un point en mouvement rectiligne uniforme ?
- 05. L'expression de la vitesse d'un point en mouvement rectiligne uniforme ?
- 06. L'accélération d'un point en mouvement rectiligne uniforme ?
- 07. Mouvement rectiligne uniforme : exercices ?
- 08. Mouvement rectiligne uniforme : les forces de frottement ?
- 09. L'application du mouvement rectiligne uniforme à la propagation de lumière ?
La réalité de nos itinéraires est rarement rectiligne.
Patrice Lepage
D'une voiture au trait d'un crayon, les mouvements sont, au quotidien, partout, tout le temps ! C'est la raison pour laquelle il est passionnant de les étudier de plus près.
En physique, un mouvement rectiligne peut avoir plusieurs formes : il peut être circulaire, curviligne, ou rectiligne. Dans le cas d'un mouvement rectiligne, parfois appelé "mouvement cinématique", le support est une droite. Mais ce mouvement peut être uniformément varié ou uniforme.
Dans le cas d'un mouvement uniforme, la notion de constance est l'une des clés de compréhension pour en saisir tous les rouages. Mais une telle notion est plus riche qu'il n'y paraît !
Voici tout ce qu'il faut savoir sur le mouvement rectiligne uniforme !
| Caractéristique | Mouvement Uniforme Rectiligne (MUR) | Mouvement Uniformément Varié (MUV) |
|---|---|---|
| Accélération | Aucune accélération (a = 0) | Accélération constante (a ≠ 0) |
| Vitesse | Constante | Change constamment |
| Trajectoire | Toujours droite | Peut être courbe |
| Équation de mouvement | x(t) = x₀ + vt | x(t) = x₀ + v₀t + (1/2)at² |
| Exemples | Voiture sur route droite | Chute libre d'un objet |

Les mouvements rectilignes, qu'est-ce que c'est ? ?

Un mouvement est dit rectiligne s'il s'effectue selon une trajectoire qui est une droite par rapport à un référentiel.
C'est le cas, par exemple, d'une voiture sur une route droite, ou de la lumière dans un milieu homogène, par rapport à un référentiel fixe.
Quelle est la condition pour qu'un mouvement rectiligne soit uniforme ? ?
Un mouvement rectiligne est dit uniforme lorsque la distance parcourue est la même chaque unité de temps. Le vecteur vitesse qui le caractérise est constant en valeur, en direction et en sens.
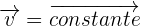
Ceci signifie également que l'objet M, suivant un mouvement rectiligne uniforme, voit sa position évoluer de la même manière par unité de temps. On peut ainsi décomposer le mouvement.
Les caractéristiques du vecteur vitesse pour un mouvement rectiligne uniforme ➡️

Le vecteur vitesse est caractérisé par :
- Sa norme constante et égale à la vitesse initiale à l'origine du mouvement : v=vo.
- Sa direction correspondant à celle du mouvement.
- Son sens : si celui-ci est le même que celui du mouvement v>0. S'il est opposé à celui du mouvement v<0.
Position d'un point en mouvement rectiligne uniforme ?

Connaissant les caractéristiques du mouvement, il est alors possible de connaître les coordonnées du point M dans le plan.
Puisque le mouvement s'effectue selon une droite, on peut choisir un repère dans lequel cette dernière coïncide avec l'axe des abscisses et avec O le centre du repère à l'origine du mouvement.
Ainsi, pour M le point en mouvement, le vecteur position (OM) n'aura qu'un abscisse de valeur x.

Dans ce cas, la vitesse du point M correspond à la dérivée de son abscisse x en fonction du temps, alors réciproquement l'abscisse x correspond à une primitive de la vitesse.
La vitesse étant constante (v=vo) sa primitive est de la forme : [x=v_{0}.t+A] où A est une constante. Déterminons alors la valeur de A : à t=0 nous avons x=x0, donc
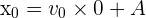 d'où [A = x_{0}]
d'où [A = x_{0}] La constante A correspond donc à l'abscisse du point M à l'origine du mouvement.
L'abscisse d'un point M en mouvement rectiligne uniforme est donc une fonction affine du temps de forme : [x=v_{0}.t+x_{0}]
- vo est la vitesse du point
- x0 l'abscisse à t = 0
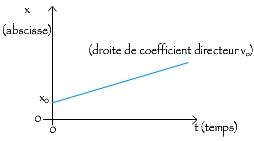
✏️ Remarques
- Si x0=0 alors l'abscisse x est une fonction linéaire du temps (x=vot).
- Si la vitesse est orientée dans le même sens que l'axe des abscisses, alors vo>o et l'abscisse est une fonction croissante.
- Si la vitesse est orientée dans le sens inverse de l'axe des abscisses, alors vo<o et l'abscisse est une fonction décroissante.
L'expression de la vitesse d'un point en mouvement rectiligne uniforme ?
Il ne faut jamais aller plus vite que sa vitesse.
Philippe Labro
Dans le même repère, les coordonnées du vecteur vitesse d'un point en mouvement rectiligne uniforme sont définis de la manière suivante :
- La vitesse est la dérivée du point x en fonction du temps. Cela se traduit graphiquement par la relation suivante :
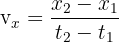
L'accélération d'un point en mouvement rectiligne uniforme ?
L'accélération correspond à la dérivée par rapport au temps de la vitesse. Cette dernière étant constante alors sa dérivée est nulle.
L'accélération est donc nulle : a=0
Mouvement rectiligne uniforme : exercices ?

Deux métros circulent en sens opposés entre les stations Louvre-Rivoli et Chêtelet les Halles, séparées de 1 km.
On supposera que les rails du métro sont en ligne droite entre les deux stations.
- Le métro 1 effectuant le trajet dans le sens Louvre-Rivoli vers Châtelet est bondé et roule à 15 km/h,
- Le métro 2 effectuant le trajet dans l'autre sens est vide et ne prend pas de voyageur. Il roule à 35 km/h.
À quelle distance de la station Louvres-Rivoli les trains vont-ils se croiser ?
Si ce problème peut sembler compliqué au premier abord, il est assez simple à résoudre à l'aide des équations des positions en fonction du temps.
Solution ?
- Appelons M1 le métro 1 d'abscisse x1 et M2 le métro 2 d'abscisse x2.
- Les équations des positions de M1 et M2 sont les suivantes : [x_{1}= v_{1}.t+x_{01}] [x_{2}=- v_{2}.t+x_{02}] car M2 circule en sens opposé à l'axe des abscisses.
- Les métros se croiseront pour x1= x2
- On obtient donc une équation avec trois inconnus : t, x01 et x02. Il y a, pour le moment, trop d'inconnues pour pouvoir la résoudre. Cependant nous pouvons exprimer x02 en fonction de x01 car nous les savons distants de 1 km : [x_{02}=x_{01}+1] Nous choisissons que x01 est égale à 0 car c'est notre point de référence du mouvement, et que nous avons choisi comme origine à notre repère.
- On obtient donc l'équation suivante, simple à résoudre : [v_{1}.t=-v_{2}.t+1 ] soit [15.t=-35.t+1 ] d'où [t=0.02].
- Les deux métros se croisent au bout de 0.02 h soit 1.2 min.
- Pour répondre à la question initiale, il suffit maintenant de connaître x1 (ou x2 puisqu'ils sont identiques) :
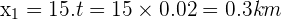
Les deux métros se croisent à 300 m de la station Louvre-Rivoli.
Et voici, en bonus, un autre exercice pour s'entraîner en vidéo :
Mouvement rectiligne uniforme : les forces de frottement ?
Un mouvement ne sera plus uniforme si des forces frottements viennent contrebalancer la vitesse initiale de l'objet, sauf si elles sont compensées par une force motrice.
Reprenons l'exemple de la voiture : le conducteur est obligé de maintenir la pédale de l'accélérateur pour maintenir une vitesse constante. Paradoxalement, l'accélération reste nulle.
En effet, le frottement des pneus sur le bitume ainsi que la résistance de l'air s'opposent à sa vitesse initiale. Dans les exercices de mécanique au niveau lycée, les forces de frottements sont souvent négligées car difficiles à appréhender.
En réalité, ces forces sont toujours présentes, sinon les objets présenteraient un mouvement perpétuel.
Jusqu'au XVIIIe, la découverte d'une machine ou d'un instrument au mouvement perpétuel était considéré comme le Graal pour de nombreux scientifiques étudiant la mécanique.

En effet ces derniers cherchaient à produire un mouvement uniforme non alimenté par des forces motrices.
C'est en
que l'Académie des sciences décide de ne plus étudier les machines au prétendu mouvement perpétuel, officialisant ainsi l'impossibilité d'un tel mouvement sur Terre.
Cette impossibilité avait déjà été établie depuis longtemps par certains scientifiques, dont Galilée. Même si l'on sait le mouvement perpétuel impossible dans l'atmosphère.
La plupart de nos moyens de transport (voitures, trains, avions...) sont étudiés de manière à limiter au maximum les forces de frottement (résistance de l'air, contact avec rails ou route).
@epicurieux Avant de partir sur les chapeaux de roues, levez le pied et apprenez en plus sur l'adhérence des pneus ! #Epicurieux #Jamy #vulgarisation #technologie #voiture #automobile #michelin #tiktokacademy #tiktokacademy ♬ son original - Jamy - Epicurieux
Les forces motrices à apporter pour maintenir un mouvement rectiligne uniforme sont donc réduites au maximum, ce qui permet des économies d'énergie.
Ainsi, les pneus des vélos de route sont extrêmement fins, les pneus des Formule 1 sont le plus lisses possible, le design des voitures de sports est profilé afin qu'elles "fendent" l'air... Simple, logique !
L'application du mouvement rectiligne uniforme à la propagation de lumière ?

Les rayons lumineux sont la résultante de la propagation de l'énergie lumineuse, mais attention, il n'ont pas de réelle existence physique.
Dans un milieu homogène donné, ces rayons lumineux se propagent selon un mouvement rectiligne et uniforme. Cette propriété est à l'origine de l'optique géométrique.
L'optique géométrique est ce qui permet d'étudier la trajectoire des rayons lumineux, mais aussi, par extension, leurs déviations, et la manière dont les images se forment.
C'est ainsi qu'un mètre laser permet de mesurer les dimensions d'une pièce d'un logement avec une grande précision.
En effet le rayon lumineux qui se propage à une vitesse connue (la vitesse de la lumière dans l'atmosphère), "sort" du laser en x1 à t0, puis est réfléchi sur le mur en face du mesureur en x2 et "reviens" sur le mètre qui capte le rayon réfléchi toujours en x1 mais t1. Le mètre mesure t1-t0 à l'aide d'un chronomètre.
Ainsi, en appliquant l'équation de l'abscisse du vecteur vitesse le mètre calcul x2-x1 et affiche la distance qui le sépare du mur.
Voici quelques exemples de temps de parcours du lasers en fonction de la distance mesurée :
| Distance en mètres | 20 | 15 | 10 | 5 | 2 |
|---|---|---|---|---|---|
| Temps de parcours du laser en pico secondes | 133.4 | 100.0 | 66.7 | 33.3 | 13.3 |
On remarque alors que le chronomètre doit être très précis pour obtenir une mesure fiable pour de petites distances. Étant donné que la vitesse de la lumière varie en fonction du milieu de propagation, le mètre laser est paramétré pour fonctionner dans un milieu donné.
À présent, vous voici avec toutes les cartes en main pour tout comprendre des mouvements rectilignes uniformes. Place aux mouvements rectilignes uniformément variés !
Résumer avec l'IA :























Si vous désirez une aide personnalisée, contactez dès maintenant l’un de nos professeurs !
j’ai aimer
Merci pour tout l’aide
J’ai un problème pour les mvt circulaire
Bonjour, pour tout soutien scolaire n’hésitez pas à consulter nos professeurs qui seront ravis de vous aider :)
J’ai aimé
Thank, very much
Merci beaucoup
Merci beaucoup mais j’ai un problème au niveau de l’équation horaires
Merci pour le cour et l’exercice qui y est, ils m’ont beaucoup aidé.